ReentrantLock和AQS

　　AQS（AbstractQueuedSynchronizer）是JDK1.5提供的一个用来构建锁和同步工具的框架，子类包括常用的ReentrantLock、CountDownLatch、Semaphore等。

　　AQS没有锁之类的概念，它有个state变量，是个int类型 ，state 是同步状态位，具体是否能够获取锁就是通过修改state来实现

　　AQS的功能可以分为独占和共享，ReentrantLock实现了独占功能

ReentrantLock锁的架构：

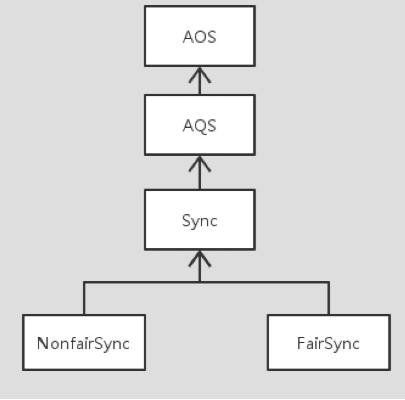
　　ReentrantLock的内部类Sync继承了AQS，分为公平锁FairSync和非公平锁NonfairSync。

获取锁的过程：

　　线程去竞争一个锁，可能成功也可能失败。成功就直接持有资源，不需要进入队列；失败的话进入队列阻塞，等待唤醒后再尝试竞争锁。

公平锁尝试获取锁：

 final void lock() { acquire(1);}

 public final void acquire(int arg) {
     if (!tryAcquire(arg) &&
         acquireQueued(addWaiter(Node.EXCLUSIVE), arg))
         selfInterrupt();
 }

 protected final boolean tryAcquire(int acquires) {
    final Thread current = Thread.currentThread();
    int c = getState();
    if (c == 0) {
        if (!hasQueuedPredecessors() &&
            compareAndSetState(0, acquires)) {
            setExclusiveOwnerThread(current);
            return true;
        }
    }
    else if (current == getExclusiveOwnerThread()) {
        int nextc = c + acquires;
        if (nextc < 0)
            throw new Error("Maximum lock count exceeded");
        setState(nextc);
        return true;
    }
    return false;
 }

　　第一个if判断AQS的state是否等于0，表示锁没有人占有。

　　接着，hasQueuedPredecessors判断队列是否有排在前面的线程在等待锁，没有的话调用compareAndSetState使用cas的方式修改state，将0改为1。

　　最后线程获取锁成功，setExclusiveOwnerThread将线程记录为独占锁的线程。

　　第二个if判断当前线程是否为独占锁的线程，因为ReentrantLock是可重入的，线程可以不停地lock来增加state的值，对应地需要unlock来解锁，直到state为零。

　　如果最后获取锁失败，下一步需要将线程加入到等待队列。

线程进入等待队列：

　　AQS内部有一条双向队列存放等待线程，节点是Node对象。每个Node维护了线程、前后Node的指针和等待状态等参数。

　　线程在加入队列之前，需要包装进Node，调用方法是addWaiter。

　　每个Node需要标记是独占的还是共享的，由传入的mode决定，ReentrantLock自然是使用独占模式Node.EXCLUSIVE。

　　创建好Node后，如果队列不为空，使用cas的方式将Node加入到队列尾。注意，这里只执行了一次修改操作，并且可能因为并发的原因失败。因此修改失败的情况和队列为空的情况，需要进入enq()方法。

阻塞等待线程:

　　线程加入队列后，下一步是调用acquireQueued阻塞线程。

非公平锁获取锁：

 final void lock() {
     if (compareAndSetState(0, 1))
         setExclusiveOwnerThread(Thread.currentThread());
     else
         acquire(1);
 }

　　在NonfairSync的lock方法里，第一步直接尝试将state修改为1，很明显，这是抢先获取锁的过程。如果修改state失败，则和公平锁一样，调用acquire。

　　公平锁会关注队列里排队的情况，老老实实按照FIFO的次序；非公平锁只要有机会就抢占，才不管排队的事。

羊群效应：

　　当有多个线程去竞争同一个锁的时候，假设锁被某个线程占用，那么如果有成千上万个线程在等待锁，有一种做法是同时唤醒这成千上万个线程去去竞争锁，这个时候就发生了羊群效应，海量的竞争必然造成资源的剧增和浪费，因此终究只能有一个线程竞争成功，其他线程还是要老老实实的回去等待。

　　AQS的FIFO的等待队列给解决在锁竞争方面的羊群效应问题提供了一个思路：保持一个FIFO队列，队列每个节点只关心其前一个节点的状态，线程唤醒也只唤醒队头等待线程。其实这个思路已经被应用到了分布式锁的实践中，见：Zookeeper分布式锁的改进实现方案。