C. Permutation Cycle

For a permutation P[1... N] of integers from 1 to N, function f is defined as follows:

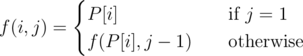
Let g(i) be the minimum positive integer j such that f(i, j) = i. We can show such j always exists.

For given N, A, B, find a permutation P of integers from 1 to N such that for 1 ≤ i ≤ N, g(i) equals either A or B.

Input

The only line contains three integers N, A, B (1 ≤ N ≤ 106, 1 ≤ A, B ≤ N).

Output

If no such permutation exists, output -1. Otherwise, output a permutation of integers from 1 to N.

Examples

input

Copy

9 2 5

output

6 5 8 3 4 1 9 2 7

input

Copy

3 2 1

output

1 2 3 

Note

In the first example, g(1) = g(6) = g(7) = g(9) = 2 and g(2) = g(3) = g(4) = g(5) = g(8) = 5

In the second example, g(1) = g(2) = g(3) = 1

这题就是求 Ax+By=N 是否存在非负解，且 x,y解就是A,B的组数，每组将最前面的数丢到最后即可

扩展欧几里得求不定方程

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define inf 2147483647
const ll INF = 0x3f3f3f3f3f3f3f3fll;
#define ri register int
template <class T> inline T min(T a, T b, T c)
{
    return min(min(a, b), c);
}
template <class T> inline T max(T a, T b, T c)
{
    return max(max(a, b), c);
}
template <class T> inline T min(T a, T b, T c, T d)
{
    return min(min(a, b), min(c, d));
}
template <class T> inline T max(T a, T b, T c, T d)
{
    return max(max(a, b), max(c, d));
}
#define scanf1(x) scanf("%d", &x)
#define scanf2(x, y) scanf("%d%d", &x, &y)
#define scanf3(x, y, z) scanf("%d%d%d", &x, &y, &z)
#define scanf4(x, y, z, X) scanf("%d%d%d%d", &x, &y, &z, &X)
#define pi acos(-1)
#define me(x, y) memset(x, y, sizeof(x));
#define For(i, a, b) for (int i = a; i <= b; i++)
#define FFor(i, a, b) for (int i = a; i >= b; i--)
#define bug printf("***********\n");
#define mp make_pair
#define pb push_back
const int N = ;
// name*******************************
ll n,a,b;
ll x0,y0;

// function******************************
ll exgcd(ll a,ll b,ll &x,ll &y)
{
    if(b==)
    {
        x=;
        y=;
        return a;
    }
    ll g=exgcd(b,a%b,x,y);
    ll t=x;
    x=y;
    y=t-(a/b)*y;
    return g;
}

//***************************************
int main()
{
//    ios::sync_with_stdio(0);
//    cin.tie(0);
    // freopen("test.txt", "r", stdin);
    //  freopen("outout.txt","w",stdout);
    cin>>n>>a>>b;
    ll g=exgcd(a,b,x0,y0);
    ll k1=x0*n/g,k2=y0*n/g;
    ll t=;
    ll a1=a,b1=b;
    a/=g;  //求通解时这里的a,b一定要除以最大公约数！！！
    b/=g;
    if(n%g)
    {
        cout<<-;
        return ;
    }

    if(k1<)
    {
        t=(-k1)/b;
        if((-k1)%b)t++;
        if(k2-a*t<)
        {
            cout<<-;
            return ;
        }
        k1+=b*t;
        k2-=a*t;
    }
    if(k2<)
    {
        t=(-k2)/a;
        if((-k2)%a)t++;
        if(k1-b*t<)
        {
            cout<<-;
            return ;
        }
        k2+=a*t;
        k1-=b*t;
    }

    queue<ll>q;
    For(i,,n)
    {
        q.push(i);
    }
    For(i,,k1)
    {
        ll x=q.front();
        q.pop();
        For(j,,a1-)
        {
            cout<<q.front()<<" ";
            q.pop();
        }
        cout<<x<<" ";
    }
    For(i,,k2)
    {
        ll x=q.front();
        q.pop();
        For(j,,b1-)
        {
            cout<<q.front()<<" ";
            q.pop();
        }
        cout<<x<<" ";
    }

    return ;
}