StanFord ML 笔记 第九部分
第九部分:
1.高斯混合模型
2.EM算法的认知
1.高斯混合模型
之前博文已经说明:http://www.cnblogs.com/wjy-lulu/p/7009038.html
2.EM算法的认知
2.1理论知识之前已经说明:http://www.cnblogs.com/wjy-lulu/p/7010258.html
2.2公式的推导
2.2.1. Jensen不等式
回顾优化理论中的一些概念。设f是定义域为实数的函数,如果对于所有的实数x,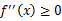 ,那么f是凸函数。当x是向量时,如果其hessian矩阵H是半正定的(
,那么f是凸函数。当x是向量时,如果其hessian矩阵H是半正定的(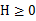 ),那么f是凸函数。如果
),那么f是凸函数。如果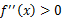 或者
或者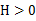 ,那么称f是严格凸函数。
,那么称f是严格凸函数。
Jensen不等式表述如下:
如果f是凸函数,X是随机变量,那么
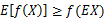
特别地,如果f是严格凸函数,那么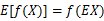 当且仅当
当且仅当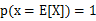 ,也就是说X是常量。
,也就是说X是常量。
这里我们将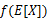 简写为
简写为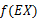 。
。
如果用图表示会很清晰:
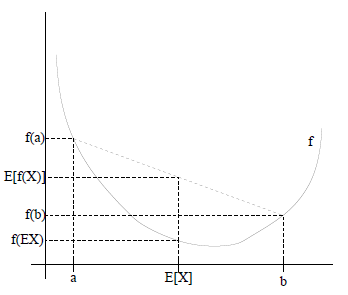
图中,实线f是凸函数,X是随机变量,有0.5的概率是a,有0.5的概率是b。(就像掷硬币一样)。X的期望值就是a和b的中值了,图中可以看到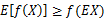 成立。
成立。
当f是(严格)凹函数当且仅当-f是(严格)凸函数。
Jensen不等式应用于凹函数时,不等号方向反向,也就是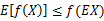 。
。
2.2.2 EM算法
给定的训练样本是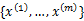 ,样例间独立,我们想找到每个样例隐含的类别z,能使得p(x,z)最大。p(x,z)的最大似然估计如下:
,样例间独立,我们想找到每个样例隐含的类别z,能使得p(x,z)最大。p(x,z)的最大似然估计如下:
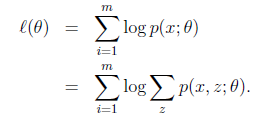

第一步是对极大似然取对数,第二步是对每个样例的每个可能类别z求联合分布概率和。但是直接求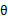 一般比较困难,因为有隐藏变量z存在,但是一般确定了z后,求解就容易了。
一般比较困难,因为有隐藏变量z存在,但是一般确定了z后,求解就容易了。
EM是一种解决存在隐含变量优化问题的有效方法。竟然不能直接最大化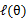 ,我们可以不断地建立
,我们可以不断地建立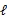 的下界(E步),然后优化下界(M步)。这句话比较抽象,看下面的。
的下界(E步),然后优化下界(M步)。这句话比较抽象,看下面的。
对于每一个样例i,让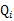 表示该样例隐含变量z的某种分布,
表示该样例隐含变量z的某种分布,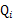 满足的条件是
满足的条件是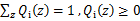 。(如果z是连续性的,那么
。(如果z是连续性的,那么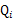 是概率密度函数,需要将求和符号换做积分符号,这里概率论书上也有说明,看个例子大家就明白)。比如要将班上学生聚类,假设隐藏变量z是身高,那么就是连续的高斯分布。如果按照隐藏变量是男女,那么就是伯努利分布了。这里就是上面说的Z的概率和为1.
是概率密度函数,需要将求和符号换做积分符号,这里概率论书上也有说明,看个例子大家就明白)。比如要将班上学生聚类,假设隐藏变量z是身高,那么就是连续的高斯分布。如果按照隐藏变量是男女,那么就是伯努利分布了。这里就是上面说的Z的概率和为1.
可以由前面阐述的内容得到下面的公式:
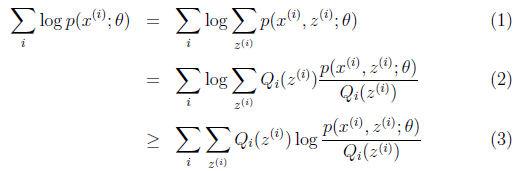
(1)到(2)比较直接,就是分子分母同乘以一个相等的函数。(2)到(3)利用了Jensen不等式,考虑到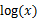 是凹函数(二阶导数小于0),而且
是凹函数(二阶导数小于0),而且
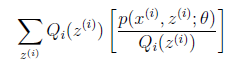
就是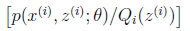 的期望(回想期望公式中的Lazy Statistician规则):
的期望(回想期望公式中的Lazy Statistician规则):
Lazy Statistician:这个公式没啥稀奇的,就是连续概率函数的期望公式,每本概率论书上都有的!
|
设Y是随机变量X的函数 (1) X是离散型随机变量,它的分布律为
(2) X是连续型随机变量,它的概率密度为
|
对应于上述问题,Y是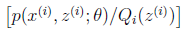 ,X是
,X是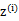 ,
,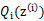 是
是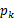 ,g是
,g是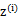 到
到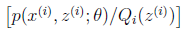 的映射。这样解释了式子(2)中的期望,再根据凹函数时的Jensen不等式:
的映射。这样解释了式子(2)中的期望,再根据凹函数时的Jensen不等式:
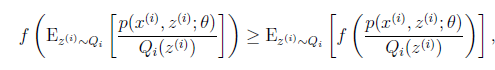
可以得到(3)。
注释:这里(3)的推到没有什么捷径,大家动手一下就可以了,连续函数的期望+Log函数性质+Jensen不等式,运用这三个公式去推导!
这个过程可以看作是对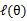 求了下界。对于
求了下界。对于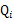 的选择,有多种可能,那种更好的?假设
的选择,有多种可能,那种更好的?假设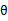 已经给定,那么
已经给定,那么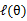 的值就决定于
的值就决定于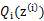 和
和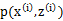 了。我们可以通过调整这两个概率使下界不断上升,以逼近
了。我们可以通过调整这两个概率使下界不断上升,以逼近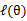 的真实值,那么什么时候算是调整好了呢?当不等式变成等式时,说明我们调整后的概率能够等价于
的真实值,那么什么时候算是调整好了呢?当不等式变成等式时,说明我们调整后的概率能够等价于 了。按照这个思路,我们要找到等式成立的条件。根据Jensen不等式,要想让等式成立,需要让随机变量变成常数值,这里得到:
了。按照这个思路,我们要找到等式成立的条件。根据Jensen不等式,要想让等式成立,需要让随机变量变成常数值,这里得到:
注释:开投的Jensen正面已经有说明!
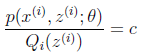
c为常数,不依赖于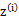 。对此式子做进一步推导,我们知道
。对此式子做进一步推导,我们知道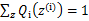 ,那么也就有
,那么也就有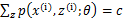 ,(多个等式分子分母相加不变,这个认为每个样例的两个概率比值都是c),那么有下式:
,(多个等式分子分母相加不变,这个认为每个样例的两个概率比值都是c),那么有下式:

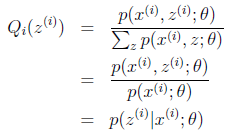
此,我们推出了在固定其他参数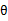 后,
后,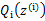 的计算公式就是后验概率,解决了
的计算公式就是后验概率,解决了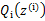 如何选择的问题。这一步就是E步,建立
如何选择的问题。这一步就是E步,建立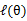 的下界。接下来的M步,就是在给定
的下界。接下来的M步,就是在给定 后,调整
后,调整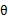 ,去极大化
,去极大化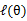 的下界(在固定
的下界(在固定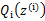 后,下界还可以调整的更大)。那么一般的EM算法的步骤如下:
后,下界还可以调整的更大)。那么一般的EM算法的步骤如下:
|
循环重复直到收敛 { (E步)对于每一个i,计算
(M步)计算
|
那么究竟怎么确保EM收敛?假定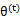 和
和 是EM第t次和t+1次迭代后的结果。如果我们证明了
是EM第t次和t+1次迭代后的结果。如果我们证明了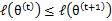 ,也就是说极大似然估计单调增加,那么最终我们会到达最大似然估计的最大值。下面来证明,选定
,也就是说极大似然估计单调增加,那么最终我们会到达最大似然估计的最大值。下面来证明,选定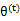 后,我们得到E步
后,我们得到E步
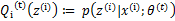
这一步保证了在给定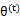 时,Jensen不等式中的等式成立,也就是
时,Jensen不等式中的等式成立,也就是
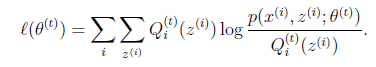
然后进行M步,固定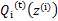 ,并将
,并将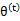 视作变量,对上面的
视作变量,对上面的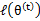 求导后,得到
求导后,得到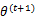 ,这样经过一些推导会有以下式子成立:
,这样经过一些推导会有以下式子成立:
注释:其实我们做的每一步都是求每个位置的局部极大值,这里肯定是大于等于前面一个值的。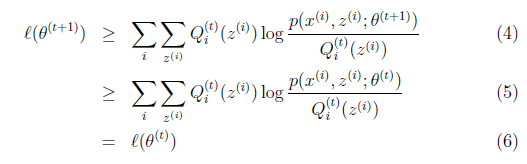
解释第(4)步,得到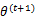 时,只是最大化
时,只是最大化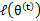 ,也就是
,也就是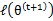 的下界,而没有使等式成立,等式成立只有是在固定
的下界,而没有使等式成立,等式成立只有是在固定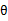 ,并按E步得到
,并按E步得到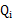 时才能成立。
时才能成立。

况且根据我们前面得到的下式,对于所有的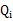 和
和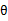 都成立
都成立
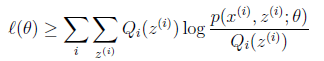
第(5)步利用了M步的定义,M步就是将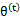 调整到
调整到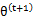 ,使得下界最大化。因此(5)成立,(6)是之前的等式结果。
,使得下界最大化。因此(5)成立,(6)是之前的等式结果。
这样就证明了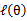 会单调增加。一种收敛方法是
会单调增加。一种收敛方法是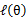 不再变化,还有一种就是变化幅度很小。
不再变化,还有一种就是变化幅度很小。
再次解释一下(4)、(5)、(6)。首先(4)对所有的参数都满足,而其等式成立条件只是在固定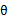 ,并调整好Q时成立,而第(4)步只是固定Q,调整
,并调整好Q时成立,而第(4)步只是固定Q,调整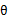 ,不能保证等式一定成立。(4)到(5)就是M步的定义,(5)到(6)是前面E步所保证等式成立条件。也就是说E步会将下界拉到与
,不能保证等式一定成立。(4)到(5)就是M步的定义,(5)到(6)是前面E步所保证等式成立条件。也就是说E步会将下界拉到与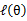 一个特定值(这里
一个特定值(这里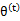 )一样的高度,而此时发现下界仍然可以上升,因此经过M步后,下界又被拉升,但达不到与
)一样的高度,而此时发现下界仍然可以上升,因此经过M步后,下界又被拉升,但达不到与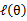 另外一个特定值一样的高度,之后E步又将下界拉到与这个特定值一样的高度,重复下去,直到最大值。
另外一个特定值一样的高度,之后E步又将下界拉到与这个特定值一样的高度,重复下去,直到最大值。
如果我们定义
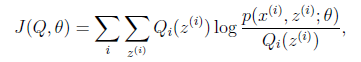
从前面的推导中我们知道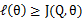 ,EM可以看作是J的坐标上升法,E步固定
,EM可以看作是J的坐标上升法,E步固定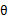 ,优化
,优化 ,M步固定
,M步固定 优化
优化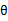 。
。
参考:https://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html#2103308
StanFord ML 笔记 第九部分的更多相关文章
- StanFord ML 笔记 第三部分
第三部分: 1.指数分布族 2.高斯分布--->>>最小二乘法 3.泊松分布--->>>线性回归 4.Softmax回归 指数分布族: 结合Ng的课程,在看这篇博文 ...
- StanFord ML 笔记 第八部分
第八部分内容: 1.正则化Regularization 2.在线学习(Online Learning) 3.ML 经验 1.正则化Regularization 1.1通俗解释 引用知乎作者:刑无刀 ...
- StanFord ML 笔记 第五部分
1.朴素贝叶斯的多项式事件模型: 趁热打铁,直接看图理解模型的意思:具体求解可见下面大神给的例子,我这个是流程图. 在上篇笔记中,那个最基本的NB模型被称为多元伯努利事件模型(Multivariate ...
- StanFord ML 笔记 第一部分
本章节内容: 1.学习的种类及举例 2.线性回归,拟合一次函数 3.线性回归的方法: A.梯度下降法--->>>批量梯度下降.随机梯度下降 B.局部线性回归 C.用概率证明损失函数( ...
- StanFord ML 笔记 第十部分
第十部分: 1.PCA降维 2.LDA 注释:一直看理论感觉坚持不了,现在进行<机器学习实战>的边写代码边看理论
- StanFord ML 笔记 第六部分&&第七部分
第六部分内容: 1.偏差/方差(Bias/variance) 2.经验风险最小化(Empirical Risk Minization,ERM) 3.联合界(Union bound) 4.一致收敛(Un ...
- StanFord ML 笔记 第四部分
第四部分: 1.生成学习法 generate learning algorithm 2.高斯判别分析 Gaussian Discriminant Analysis 3.朴素贝叶斯 Navie Baye ...
- StanFord ML 笔记 第二部分
本章内容: 1.逻辑分类与回归 sigmoid函数概率证明---->>>回归 2.感知机的学习策略 3.牛顿法优化 4.Hessian矩阵 牛顿法优化求解: 这个我就不记录了,看到一 ...
- (转载)[机器学习] Coursera ML笔记 - 监督学习(Supervised Learning) - Representation
[机器学习] Coursera ML笔记 - 监督学习(Supervised Learning) - Representation http://blog.csdn.net/walilk/articl ...
随机推荐
- pyhanlp 共性分析与短语提取内容详解
pyhanlp 共性分析与短语提取内容详解 简介 HanLP中的词语提取是基于互信息与信息熵.想要计算互信息与信息熵有限要做的是 文本分词进行共性分析.在作者的原文中,有几个问题,为了便于说明,这 ...
- IText简介及示例
一.iText简介 iText是著名的开放源码的站点sourceforge一个项目,是用于生成PDF文档的一个java类库.通过iText不仅可以生成PDF或rtf的文档,而且可以将XML.Html文 ...
- 排序算法<No.2>【快速排序】
最近因为项目需要,研究AI相关的东西,主要是算法相关的. 有感触,所以决定,来一个系列的博文,可能会耗时很久,那就是要完成算法系列.起点,从最常用最基本的排序开始.后续会跟进其他类型的,比如树,图等领 ...
- PerformEraseBackground 擦除背景(ThemeServices)
PerformEraseBackground 擦除背景的简单方法(外带ThemeServices例子) 在查这个函数的时候,顺便看到了有趣的代码. 怎么使用 Themes . unit Unit2; ...
- RedirectStandardOutput
当Process将文本写入其标准流,通常在控制台上显示文本. 通过设置RedirectStandardOutput到true重定向StandardOutput流,可以操作或取消进程的输出. 例如,可以 ...
- centos7系列-给普通用户sudo权限
对于linux用户来讲,普通用户的权限是有一定限制的,所以在有些操作的时候,是需要sudo权限的,那么如何在linux下赋予普通用户sudo权限呢?此处将讲解一下方法. 在login我们的系统后,如果 ...
- 【mysql】mysql表分区、索引的性能测试
概述 mysql分区表概述:google搜索一下: RANGE COLUMNS partitioning 主要测试mysql分区表的性能: load 500w 条记录:大约在10min左右: batc ...
- JVM异常之:堆溢出OutofMemoryError
1.堆溢出 Java 堆内存的OutOfMemoryError异常是实际应用中最常见的内存溢出异常情况.出现Java 堆内存溢出时,异常堆栈信息“java.lang.OutOfMemoryError” ...
- ubuntu 间简单相互通信
1. nc 命令 在一台机器上运行nc -l 来监听本机的2222号端口 另外一台机器就能连接到这台监听的机器上,假设上面那台机器的ip是192. nc 之后就能互相发送字符了 2. iptux通 ...
- 项目中自己一直用到的baseAdapter的类
import java.util.LinkedList; import java.util.List; import android.content.Context; import android.v ...

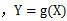 (g是连续函数),那么
(g是连续函数),那么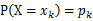 ,k=1,2,…。若
,k=1,2,…。若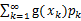 绝对收敛,则有
绝对收敛,则有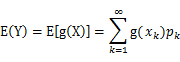
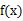 ,若
,若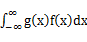 绝对收敛,则有
绝对收敛,则有