DP斜率优化总结

DP斜率优化总结

任务安排1

首先引入一道题，先$O(N^2)$做法：分别预处理出$T_i,C_i$前缀和$t[i],c[i]$，设$f[i]$，其中$f[i]$并不表示前$i$个任务花费的时间，而是壳含前面所有决策对于后面的影响。这道题dp思路就是边决策边加上当前决策对于后面的影响（一种“费用提前计算”的思想）

转移方程：

\[f[i]=min(f[j]+(c[i]-c[j])*t[i]+s*(c[n]-c[j]), f[i])
\]

#include <cstdio>

#include <cstring>

#define MIN(A,B) ((A)<(B)?(A):(B))

#define MAXN 5005

using namespace std;

int f[MAXN];

int sumt[MAXN],sumc[MAXN];

int n,s;

int main(){

    memset(f, 0x3f, sizeof(f));

    f[0]=0;

    scanf("%d\n%d", &n, &s);

    for(int i=1;i<=n;++i){

        int t,c;

        scanf("%d %d", &t, &c);

        sumt[i]=sumt[i-1]+t;

        sumc[i]=sumc[i-1]+c;

    }

    for(int i=1;i<=n;++i)

    for(int j=0;j<i;++j){

        f[i]=MIN(f[j]+(sumc[i]-sumc[j])*sumt[i]+s*(sumc[n]-sumc[j]), f[i]);

    }

    printf("%d", f[n]);

    return 0;

}

任务计划2

斜率优化做法。将原转移方程移项，让只含$j$的式子移到左边，其余移到右边，再将右边含$j$的式子提公因式，得到

\[f[j]=c[j]\times (t[i]+s)+f[i]-s\times c[n]-c[i]\times t[i]
\]

此时将外层循环到的$i$看做已知量（则关于$i$的变量$t[i],c[i]$为常数），看做一个斜率确定的一次函数$y=kx+b$，其中$f[j]$看做函数的$y$，$c[j]$看做函数的$x$，$(t[i]+s)$为斜率。要让$f[i]$最小即让此一次函数截距最小。

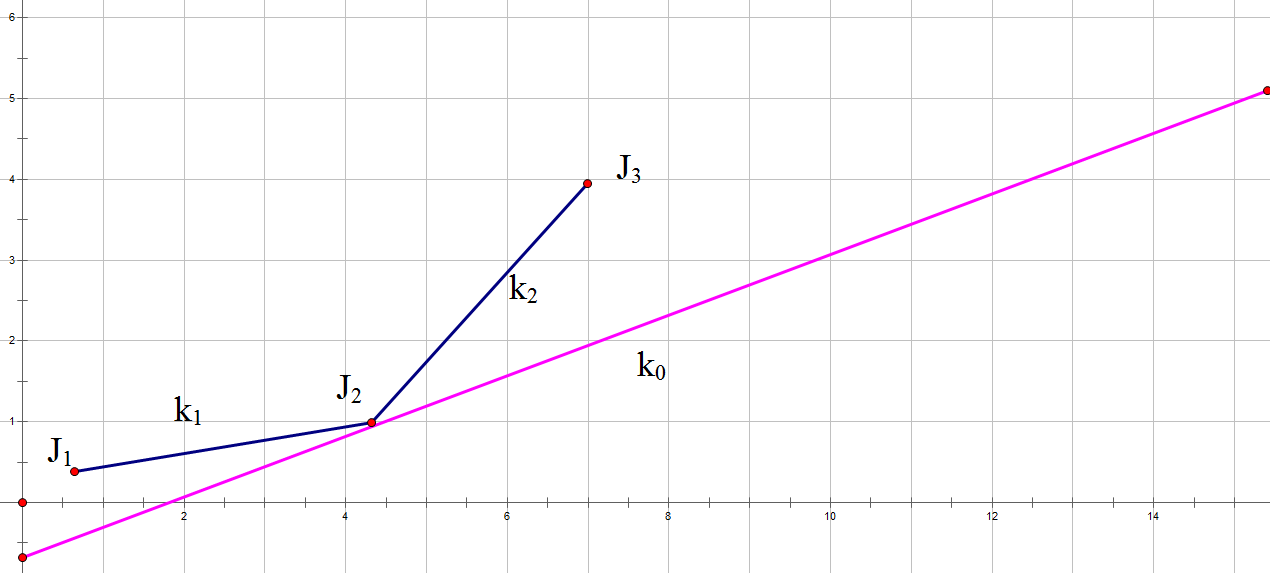
(图自ButterflyDew)

而容易得到：将此确定的斜率函数从最下面向上平移遇到的第一个点$(c[j],f[j])$就是能取到最小截距（最优$f[i]$）的点，（满足$k_1\le k_0\le k_2$），如图，也就是一个下凸壳的顶点。

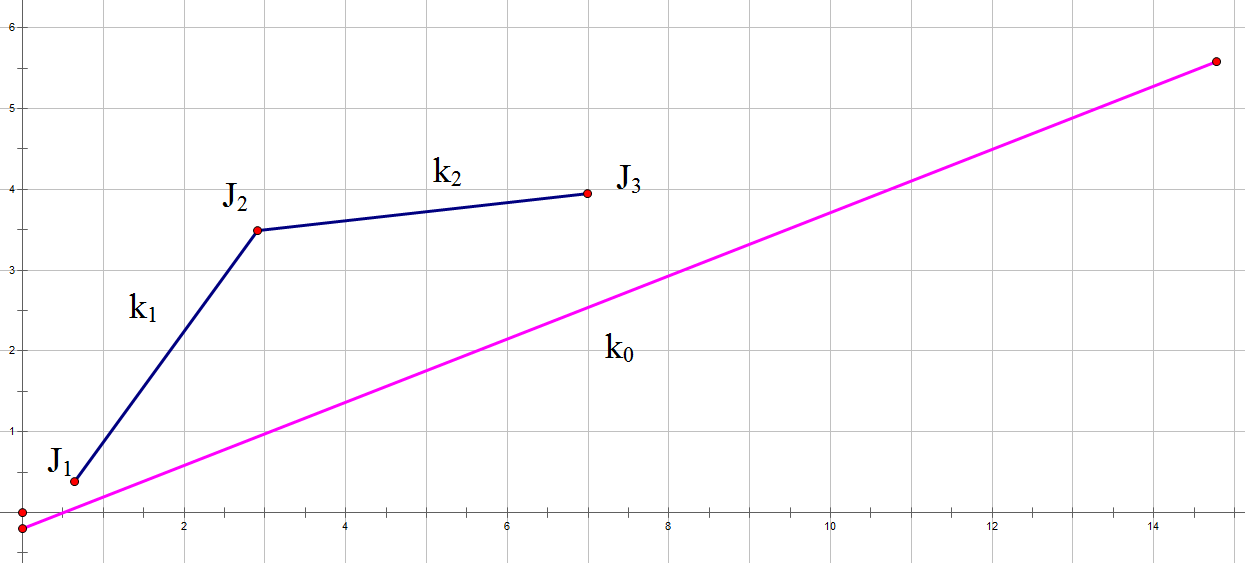
而像这样的上凸壳顶点如图显然一定不会是最优解，所以我们维护一个下凸壳，每次找到顶点即为最优。

而这道题我们不需要维护整个下凸壳，而只维护下凸壳顶点及顶点右侧的点（因为左侧不可能比顶点优）。我们维护一个单调队列，使队首为下凸壳顶点，每次最优即为队首元素。维护时先将下凸壳顶点左边的所有点弹掉（若当前点与下一个点构成的直线斜率小于等于$s+t[i]$，则当前点在左边），之后队首就是下凸壳的顶点，取出并算出的$f[i]$即为最优，最后再将所有构成上凸壳的点删去维护一下下凸壳。

单调队列部分实现代码：

while(l<r&&f[q[l+1]]-f[q[l]]<=(S+t[i])*(c[q[l+1]]-c[q[l]])) l++; // 弹出顶点左边的点

f[i]=f[q[l]]+t[i]*c[i]+S*c[n]-c[q[l]]*(S+t[i]);

while(l<r&&(f[i]-f[q[r]])*(c[q[r]]-c[q[r-1]])<=(f[q[r]]-f[q[r-1]])*(c[i]-c[q[r]])) r--; // 维护下凸壳

q[++r]=i;

完整代码：

#include <cstdio>

#include <cstring>

#define MIN(A,B) ((A)<(B)?(A):(B))

#define MAXN 5005*2

using namespace std;

int f[MAXN],q[MAXN];

int t[MAXN],c[MAXN];

int n,s;

int main(){

    memset(f, 0x3f, sizeof(f));

    f[0]=0;

    scanf("%d\n%d", &n, &s);

    for(int i=1;i<=n;++i){

        int tt,tc;

        scanf("%d %d", &tt, &tc);

        t[i]=t[i-1]+tt;

        c[i]=c[i-1]+tc;

    }

    int l=1,r=1;

    for(int i=1;i<=n;++i){

        while(l<r&&(f[q[l+1]]-f[q[l]])<=(t[i]+s)*(c[q[l+1]]-c[q[l]])) l++;

        f[i]=f[q[l]]-c[q[l]]*(t[i]+s)+s*c[n]+c[i]*t[i];

        while(l<r&&(f[q[r]]-f[q[r-1]])*(c[i]-c[q[r]])>=(f[i]-f[q[r]])*(c[q[r]]-c[q[r-1]])) r--;

        q[++r]=i;

    }

    printf("%d", f[n]);

    return 0;

}

任务安排3

因为$T_i$可能为负数，所以直线斜率$s+t[i]$不单增，所以不能直接单调队列取队首，而是二分查找出两条斜率为$k_1,k_2$的直线满足$k_1\le s+t[i]\le k_2$，两条直线交点即为最优点。

#include <cstdio>

#include <cstring>

#define MIN(A,B) ((A)<(B)?(A):(B))

#define MAXN 300003

#define ll long long

using namespace std;

ll f[MAXN];

int q[MAXN];

ll t[MAXN],c[MAXN];

int n,s;

int l=1,r=1;

inline int query(ll k){

    int L=l,R=r,ans;

    while(L<=R){

        int mid=(L+R)>>1;

        if((f[q[mid]]-f[q[mid-1]])<=k*(c[q[mid]]-c[q[mid-1]])) L=mid+1,ans=mid;

        else R=mid-1;

    }

    return q[ans];

}

int main(){

    memset(f, 0x3f, sizeof(f));

    f[0]=0;

    scanf("%d\n%d", &n, &s);

    for(int i=1;i<=n;++i){

        ll tt,tc;

        scanf("%lld %lld", &tt, &tc);

        t[i]=t[i-1]+tt;

        c[i]=c[i-1]+tc;

    }

    for(int i=1;i<=n;++i){

        int j=query(t[i]+s);

        f[i]=f[j]-c[j]*(t[i]+s)+s*c[n]+c[i]*t[i];

        while(l<r&&

              (f[q[r]]-f[q[r-1]])*(c[i]-c[q[r]])>=(f[i]-f[q[r]])*(c[q[r]]-c[q[r-1]])) r--;

        q[++r]=i;

    }

    printf("%lld", f[n]);

    return 0;

}

百日旅行

$N$天，如果连续$x$天旅游，则花费$p\times x\times x$，否则连续$x$天吃饭，花费$Q\times x$，问最小花费

设计dp，$f[i]$表示第$i$天最小花费并且这一天在旅游，$g[i]$表示在这一天吃饭，转移方程：

f[i]=min(g[j]+SQR(i-j)*p,f[i])

g[i]=min(f[j]+(i-j)*q,g[i])

观察$g[i]$，$g[i]=i*q+f[j]-j*q$，所以维护$1$到$i-1$的$f[i]-i*p$最小值即可。

观察$f[i]$，$f[i]=g[i]+p*i^2-2*p*i*j+p*j^2$

移项，使只含$j$的式子在左边，其余右边，得$g[j]+p*j^2=i*(2*p*j)+f[i]-p*i^2$

此时看做一个一次函数，$x=2*p*j,k=i,b=f[i]-p*i^2$，要想$f[i]$最小，即让截距最小，维护一个下凸壳。又发现斜率$i$单增，可使用单调队列。

#include <cstdio>

#include <algorithm>

#define ll long long

#define MAXN 200002

#define MIN(A,B) ((A)<(B)?(A):(B))

#define j (q[l])

#define SQR(A) ((A)*(A))

#define Y(A) (g[A]+P*(A)*(A))

#define X(A) ((A)*2*P)

using namespace std;

int n,l,r;

ll f[MAXN],g[MAXN],q[MAXN],P,Q;

int main(){

    scanf("%d %lld %lld", &n, &P, &Q);

    l=1,r=1;

    ll t=0;

    for(int i=1;i<=n;++i){

        while(l<r&&(Y(q[l + 1]) - Y(q[l])) <= i*(X(q[l+1]) - X(q[l]))) ++l;

        f[i]=g[j]+P*SQR(i-j);

        g[i]=i*Q+t;

        t=min(f[i]-i*Q,t);

        while(l<r && (Y(q[r]) - Y(q[r-1])) * (X(i) - X(q[r])) >= (Y(i) - Y(q[r])) * (X(q[r]) - X(q[r-1]))) --r;

        q[++r]=i;

    }

    printf("%lld", min(f[n], g[n]));

    return 0;

}

/*

g[i]=i*q+f[j]-j*q

g[j]+p*j^2=i*(2*p*j)+f[i]-p*i^2

*/