【树形背包】bzoj4033: [HAOI2015]树上染色

仔细思考后会发现和51nod1677 treecnt有异曲同工之妙

Description

有一棵点数为N的树，树边有边权。给你一个在0~N之内的正整数K，你要在这棵树中选择K个点，将其染成黑色，并

将其他的N-K个点染成白色。将所有点染色后，你会获得黑点两两之间的距离加上白点两两之间距离的和的收益。

问收益最大值是多少。

Input

第一行两个整数N,K。

接下来N-1行每行三个正整数fr,to,dis，表示该树中存在一条长度为dis的边(fr,to)。

输入保证所有点之间是联通的。

N<=2000,0<=K<=N

Output

输出一个正整数，表示收益的最大值。

Sample Input

5 2
1 2 3
1 5 1
2 3 1
2 4 2

Sample Output

17
【样例解释】
将点1,2染黑就能获得最大收益。

---

题目分析

这题目第一眼看上去根本不像是背包题吧……倒像是个贪心或者奇妙结论题。

但是可以像treecut一样，将答案按照树上每一条边来统计贡献。

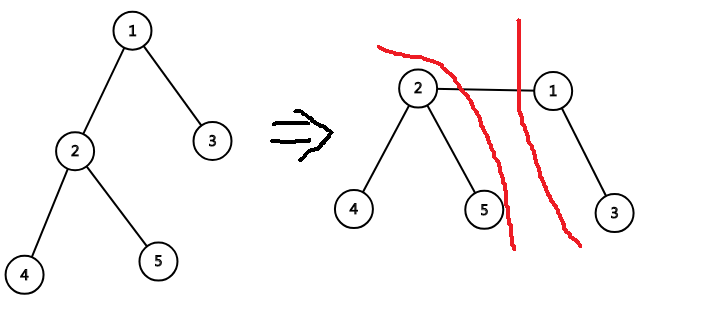
我们把一颗树沿某条边分开，看成这个样子。

那么显然若知道这条边左右两边黑白点各有多少个，就可以计算这个情况下的答案了。

也就是说，如果我们确定一条边来把树分开，那就可以依靠枚举来确定最优答案。

观察一下这个问题是具有最优子结构的，也就是说变成了一个树上背包的形式：左右两边黑白点个数的不同情况各有体积和价值，求最大价值。

我们定义$f[x][i]$表示以$x$为根的子树中，有$i$个黑点，这种情况的最大价值。

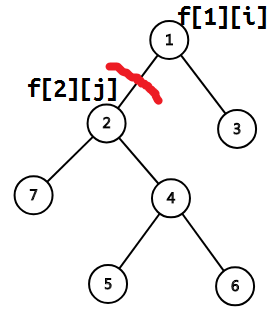
考虑如何转移。自然是要枚举上图中的$i$和$j$。然后就是背包式地转移：

 for (int j=mn; j>=; j--)
     for (int l=; l<=upp&&l<=j; l++)
     {
         ll left = 1ll*l*(k-l)*w;
         ll right = 1ll*(size[v]-l)*(n-size[v]-k+l)*w;
         f[x][j] = std::max(f[x][j], f[v][l]+f[x][j-l]+left+right);
     }

其中mn和upp表示枚举的上界。

这个把统计转化为各个边的贡献，然后转为背包做还是很妙的。

总结

一类难以通过树形结构直接转移的动态规划问题，可以考虑对于边将树划分为两个部分的子问题，再分别维护答案。

后记

隔了几天回来看又作为一个不会做这题的人表示讲的有一点不详细。

首先有一个很大的疑问是：讲是把答案拆开统计，但是到底怎么计算这个“贡献”？这个“贡献”又是什么东西？

没写过题的人看了代码肯定又有疑问：为什么统计一下点数再乘个边权就行了？

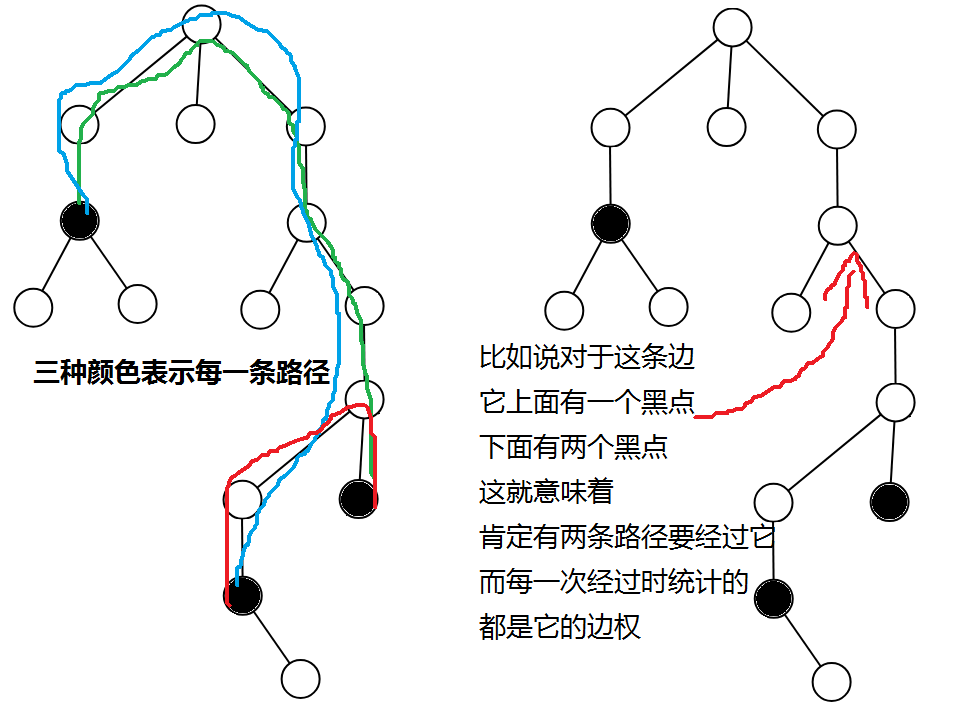
这里放张图，备忘一下

 #include<bits/stdc++.h>
 typedef long long ll;
 const int maxn = ;
 const int maxm = ;
 const ll INF = 112921504606846976ll;

 struct Edge
 {
     int y,val;
     Edge(int a=, int b=):y(a),val(b) {}
 }edges[maxm];
 int n,k;
 int size[maxn];
 int edgeTot,nxt[maxm],head[maxn];
 ll f[maxn][maxn];

 int read()
 {
     char ch = getchar();
     int num = ;
     bool fl = ;
     for (; !isdigit(ch); ch = getchar())
         if (ch=='-') fl = ;
     for (; isdigit(ch); ch = getchar())
         num = (num<<)+(num<<)+ch-;
     if (fl) num = -num;
     return num;
 }
 void dfs(int x, int fa)
 {
     size[x] = ;
     for (int i=head[x]; i!=-; i=nxt[i])
         if (edges[i].y!=fa) dfs(edges[i].y, x), size[x] += size[edges[i].y];
 }
 void addedge(int u, int v, int w)
 {
     edges[++edgeTot] = Edge(v, w), nxt[edgeTot] = head[u], head[u] = edgeTot;
 }
 void dp(int x, int fa)
 {
     f[x][] = f[x][] = ;
     if (size[x]==) return;
     int mn = std::min(k, size[x]);
     for (int i=head[x]; i!=-; i=nxt[i])
     {
         int v = edges[i].y, w=edges[i].val, upp = std::min(k, size[v]);
         if (v!=fa){
             dp(v, x);
             for (int j=mn; j>=; j--)
                 for (int l=; l<=upp&&l<=j; l++)
                 {
                     ll left = 1ll*l*(k-l)*w;
                     ll right = 1ll*(size[v]-l)*(n-size[v]-k+l)*w;
                     f[x][j] = std::max(f[x][j], f[v][l]+f[x][j-l]+left+right);
                 }
         }
     }
 }
 int main()
 {
     memset(head, -, sizeof head);
     n = read(), k = read();
     if (k<< > n) k = n-k;
     for (int i=; i<n; i++)
     {
         int u = read(), v = read(), w = read();
         addedge(u, v, w);
         addedge(v, u, w);
     }
     dfs(, );
     for (int i=; i<=n; i++)
         for (int j=; j<=size[i]; j++)
             f[i][j] = -INF;
     dp(, );
     printf("%lld\n",f[][k]);
     return ;
 }

END