【思维题】TCO14 Round 2C InverseRMQ

全网好像就只有劼和manchery写了博客的样子……；正解可能是最大流？但是仔细特判也能过

题目描述

RMQ问题即区间最值问题是一个有趣的问题。

在这个问题中，对于一个长度为 n 的排列，query(l,r) 将返回 al,⋯,ar 中的最大值。

如对于 {3,1,4,2,5}，query(2,4)=max(1,4,2)=4

现在我们给出 m 次询问的结果，问是否存在至少一个长度为 n 的排列 P 满足所有的条件。

输入格式

第一行 T

每一组数据中，第一行 n,m，接下来 m 行，每行 li,ri,ans

输出格式

T 行 Possible 或 Impossible

数据范围

对于 20% 的数据， n≤10

对于另 10% 的数据，li=ri

对于另 20% 的数据，[li,ri] 两两没有交集

对于另 20% 的数据，ansi 互不相同

对于所有数据，T≤10,n,m≤2000,1≤li≤ri≤n

时间限制 1s

空间限制 256MB

---

官方题解

先按照值从小到大排序

然后值一样的一起处理 如果交为空 无解

如果交被之前所有的并给完全包含了 无解

如果某一时刻并的大小比数字还大 无解

以上三点就是充要条件

题目分析

manchery的题解是比较详细的，但似乎漏了点什么

比如说这种情况：

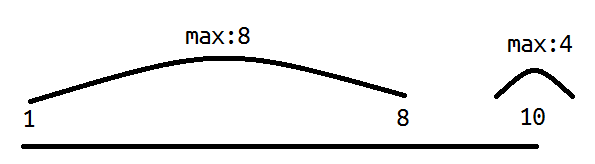
就是不可以的。

第一遍做这题的时候有考虑到两个问题：

1. 区间最大值不够这个区间用（manchery第三条条件）
2. 空余位置不足够填下剩下的数字（以上的反例）

不过由于代码能力不足，并没有打出来……

 #include<bits/stdc++.h>
 const int maxn = ;

 struct point
 {
     int l,r,c;
 }a[maxn],b[maxn],t[maxn];
 int T,n,m,stb;
 bool pot[maxn],fbd[maxn][maxn],insideConflict;

 int read()
 {
     char ch = getchar();
     int num = ;
     bool fl = ;
     for (; !isdigit(ch); ch = getchar())
         if (ch=='-') fl = ;
     for (; isdigit(ch); ch = getchar())
         num = (num<<)+(num<<)+ch-;
     if (fl) num = -num;
     return num;
 }
 int main()
 {
     T = read();
     while (T--)
     {
         memset(fbd, , sizeof fbd);
         memset(pot, , sizeof pot);
         n = read(), m = read(), insideConflict = ;
         for (int i=; i<=n; i++) a[i].l = , a[i].r = n, b[i].l = n, b[i].r = ;
         for (int i=; i<=m; i++)
         {
             int l = read(), r = read(), c = read();
             t[i].l = l, t[i].r = r, t[i].c = c;
             if (c > n||c < ) insideConflict = ;
             else{
                 pot[c] = ;
                 a[c].l = std::max(l, a[c].l), a[c].r = std::min(r, a[c].r);
                 b[c].l = std::min(l, b[c].l), b[c].r = std::max(r, b[c].r);
                 if (a[c].l > a[c].r) insideConflict = ;
             }
         }
         for (int i=; i<=n; i++)
             if (b[i].r-b[i].l+ > i){
                 insideConflict = ;
                 break;
             }
         if (insideConflict){
             puts("Impossible");
             continue;
         }
         for (int i=; i<=n; i++)
         {
             for (int j=; j<=n; j++) fbd[i][j] = fbd[i-][j];
             if (pot[i-])
                 for (int j=b[i-].l; j<=b[i-].r; j++)
                     fbd[i][j] = ;
         }
         for (int i=; i<=n; i++)
         {
             stb = ;
             for (int j=a[i].l; j<=a[i].r; j++)
                 if (!fbd[i][j]) stb = ;
             if (!stb) break;
             stb = ;
             for (int j=; j<=n; j++)
                 if (!fbd[i][j]) stb++;
             if (stb < n-i+){
                 stb = ;
                 break;
             }
         }
         if (!stb)
             puts("Impossible");
         else puts("Possible");
     }
     return ;
 }

END