hdu6069[素数筛法] 2017多校4

对于[l , r]内的每个数，根据唯一分解定理有  

所以有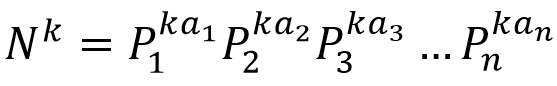 

因为    

//可根据唯一分解定理推导

所以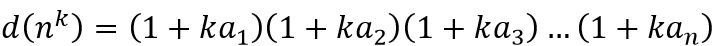     

题目要求

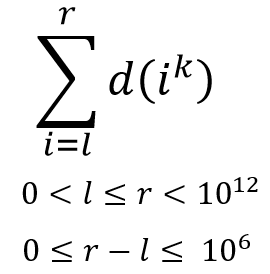
就可以运用它到上述公式

(注意不能暴力对l，r内的数一个个分解算贡献，而应该枚举l，r区间内质数的倍数):

/*hdu6069[素数筛法] 2017多校3*/
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
LL l, r, k;
const LL MOD = 998244353LL;
int T, n, prime[], primesize;
bool isprime[];
void getlist(int listsize)
{
    memset(isprime, , sizeof(isprime));
    isprime[] = false;
    for (int i = ; i <= listsize; i++)
    {
        if (isprime[i])prime[++primesize] = i;
        for (int j = ; j <= primesize && i * prime[j] <= listsize; j++)
        {
            isprime[i * prime[j]] = false;
            if (i % prime[j] == )break;
        }
    }
}
LL num[], ans[];
void solve() {
    LL n = r - l + ;
    for (int i = ; i < n; i++) {
        num[i] = i + l;
        ans[i] = ;    //预处理l到r之间所有的数 和 其对答案的的贡献;
    }
    //不能枚举l到r之间的元素进行暴力质因数分解, 会超时; 所以我们可以通过枚举质数的倍数来优化。
    for (int i = ; (LL)prime[i]*prime[i] <= r; i++) {
        for (LL j = prime[i] * (l / prime[i]); j <= r; j += prime[i]) {
            if (j < l) continue;
            LL cnt = ;  //对l到r之间素数prime[i]的倍数进行质因数分解, 计算出其对答案的贡献;
            while (num[j - l] % prime[i] == ) {
                cnt++;
                num[j - l] /= prime[i];
            }
            ans[j - l] = (ans[j - l] * (1LL + cnt * k)) % MOD;
        }
    }
    LL res = ;
    for (int i = ; i < n; i++) {
        if (num[i] > ) {
            ans[i] = (ans[i] * (1LL + k)) % MOD;
        }
        res = (res + ans[i]) % MOD;
    }
    printf("%lld\n", res);
}
int main() {
    getlist();
    scanf("%d", &T);
    while (T--) {
        scanf("%lld%lld%lld", &l, &r, &k);
        solve();
    }
    return ;
}