Bzoj1479: [Nerrc1997]Puncher打孔机

1479: [Nerrc1997]Puncher打孔机

Time Limit: 5 Sec  Memory Limit: 64 MB
Submit: 22  Solved: 14
[Submit][Status][Discuss]

Description

打孔机是一种在票上打孔的装置， 假设票是一个M*N的矩阵，矩阵行列间距相等，你可以选择在M*N个位置上打穿或不打穿，这样就有 2^(M*N)-1（至少要打一个孔）不同的方案数。 但是我们的问题并不是这么简单的，如果两种方案经过如下的若干操作后，打穿的孔刚好重合，那么认为这两个方案是相同的： •翻转 •旋转0，90，180，270 •平行移动 显然如果两种方案上孔的数目不同，那么必然是不同的方案。现在你的问题就是给定M，N，算出所有不同的方案数。

Input

文件包含两个数M(≤6), N (≤10) ,用空格分开。

Output

只有一行，为所求的方案数。

Sample Input

3 3

Sample Output

85

HINT

---

题解：

　　看到这道题，没有一点思路，看了题解才知道什么叫做恶心数学题【此处D膜拜出题人】

　　我们考虑忽略平移对这道题目的影响，毕竟我们对于旋转翻转之类的比较了解，于是我们思考设立一个状态状态来包含所有置换

　　•于是我们设：

　　　　F_u-v表示u行v列的矩阵中，在其每条边上都至少有一个格子被染色，其本质不同的染色方案数。

　　　　因为每条边上都有染色的格子，所以无论向哪个方向平移，都会有染色的格子移出矩阵，所以无法进行平移操作的，那么只需要考虑翻转和旋转了。

　　•

　　　　G0_uv　   表示每条边上都至少有一个格子被染色的u行v列的矩阵，总的染色方案数。

　　　　G¹_uv　　表示每条边上都至少有一个格子被染色的u行v列的矩阵，其通过旋转180度保持不变的染色方案数。

　　　　G2_uv　　表示每条边上都至少有一个格子被染色的u行u列的矩阵，其通过旋转90度或270度保持不变的染色方案数。

　　　　G3_uv　　表示每条边上都至少有一个格子被染色的u行v列的矩阵，其通过上下翻转保持不变的染色方案数。

　　　　G4_uv　　表示每条边上都至少有一个格子被染色的u行v列的矩阵，其通过左右翻转保持不变的染色方案数。

　　　　G5_uv　　表示每条边上都至少有一个格子被染色的u行u列的矩阵，其通过沿某条对角线翻转保持不变的染色方案数。

　　　　求得所有的G值，F值就只需套用引理即可。而的求法也都大同小异。

　　•　求法：容斥原理！！！

　　　　就是应用容斥原理，将所有格子任意染色，减去第一行或者第u行或者第一列或者第v列没染色，再加上第1行和第u行均未染色……即：

　　　　

　　　　

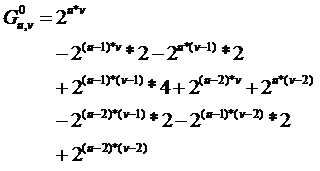
　　　　旋转180度不变，实际上就是前个格子任意染色，然后剩下的格子染色情况则由这些格子旋转得到，同样需要应用容斥原理：

　　　　

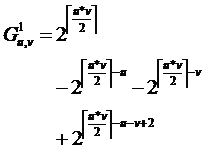
　　　　旋转90度或者270度，则是由左上角的个格子任意染色，然后剩下的格子染色情况则由这些格子旋转得到，同样需要应用容斥原理：

　　　　

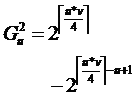
　　　　上下翻转，则是由上半部分的个格子任意染色，然后剩下的格子染色情况则由这些格子旋转得到，同样需要应用容斥原理：

　　　　

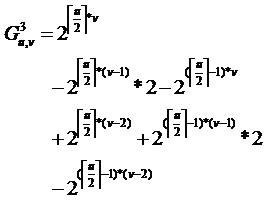
　　　　左右翻转，则是由半边部分的个格子任意染色，然后剩下的格子染色情况则由这些格子旋转得到，同样需要应用容斥原理：

　　　　

　　　　

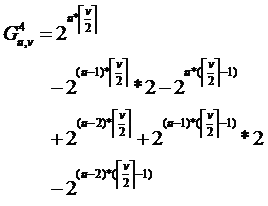
　　　　沿对角线翻转，则是由对角线上面部分的个格子任意染色，然后剩下的格子染色情况则由这些格子旋转得到，同样需要应用容斥原理：

　　　　

　　　　

 

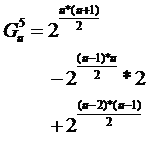
　　　　完美解决！！！

　　　　参考文献： 《Puncher》解题报告

---

 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cmath>
 #include<cstdio>
 #define ll long long
 using namespace std;
 ll ans;
 int n,m;
 int read()
 {
     int x=,f=; char ch;
     while (ch=getchar(),ch<''||ch>'') if (ch=='-') f=-;
     while (x=x*+ch-'',ch=getchar(),ch>=''&&ch<='');
     return x*f;
 }
 ll ksm(ll x,int k)
 {
     ll res=;
     for (int i=k; i; i>>=,x*=x) if (i&) res*=x;
     return res;
 }
 ll get0(int u,int v)
 {
     ll res=;
     res=ksm(,u*v)
         -ksm(,(u-)*v)*-ksm(,u*(v-))*
         +ksm(,(u-)*(v-))*+ksm(,(u-)*v)+ksm(,u*(v-))
         -ksm(,(u-)*(v-))*-ksm(,(u-)*(v-))*
         +ksm(,(u-)*(v-));
     return res;
 }
 ll get1(int u,int v)
 {
     ll res=;
     res=ksm(,ceil(u*v/2.0))
         -ksm(,ceil(u*v/2.0)-u)-ksm(,ceil(u*v/2.0)-v)
         +ksm(,ceil(u*v/2.0)-u-v+);
     return res;
 }
 ll get2(int u,int v)
 {
     ll res=;
     res=ksm(,ceil(u*v/4.0))-ksm(,(ceil(u*v/4.0)-u+));
     return res;
 }
 ll get3(int u,int v)
 {
     ll res=;
     res=ksm(,ceil(u/2.0)*v)
         -ksm(,ceil(u/2.0)*(v-))*-ksm(,(ceil(u/2.0)-)*v)
         +ksm(,ceil(u/2.0)*(v-))+ksm(,(ceil(u/2.0)-)*(v-))*
         -ksm(,(ceil(u/2.0)-)*(v-));
     return res;
 }
 ll get4(int u,int v)
 {
     ll res=;
     res=ksm(,u*ceil(v/2.0))
         -ksm(,(u-)*ceil(v/2.0))*-ksm(,u*(ceil(v/2.0)-))
         +ksm(,(u-)*ceil(v/2.0))+ksm(,(u-)*(ceil(v/2.0)-))*
         -ksm(,(u-)*(ceil(v/2.0)-));
     return res;
 }
 ll get5(int u,int v)
 {
     ll res=;
     res=ksm(,u*(u+)/2.0)-ksm(,(u-)*u/2.0)*+ksm(,(u-)*(u-)/2.0);
     return res;
 }
 ll get(int u,int v)
 {
     ll res=;
     if (v==)
     {
         if (u==) return ;
         return (ksm(,u-)+ksm(,(u+)/2.0-))/2.0;
     }
     else
     {
         if (u==v)
         {
             res=(get0(u,v)+get1(u,v)+*get2(u,v)+get3(u,v)+get4(u,v)+*get5(u,v));
             return res/;
         }
         else if (u>v)
         {
             res=(get0(u,v)+get1(u,v)+get3(u,v)+get4(u,v));
             return res/;
         }
     }
 }
 int main()
 {
     n=read(); m=read();
     for (int u=; u<=max(n,m); u++)
         for (int v=; v<=min(u,min(n,m)); v++)
         ans+=get(u,v);
     printf("%lld\n",ans);
     return ;
 }