[bzoj1009][HNOI2008]GT考试

Description

阿申准备报名参加考试，准考证号为位数,他不希望准考证号上出现不吉利的数字。
他的不吉利数学有位，不出现是指中没有恰好一段等于. 可以为.

Input

第一行输入.接下来一行输入位的数。

Output

阿申想知道不出现不吉利数字的号码有多少种，输出模取余的结果.

Sample Input

4 3 100
111

Sample Output

81

HINT

Solution

表示已填好前i位,此时匹配到的方案数.

表示现在匹配到,填下一个数后匹配到的方案数.

 .

可用预处理出.

,矩乘优化即可.

 

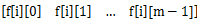
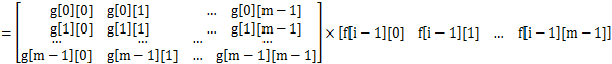
#include<set>
#include<cmath>
#include<ctime>
#include<queue>
#include<stack>
#include<cstdio>
#include<vector>
#include<string>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#define M 25
using namespace std;
struct matrix{
    int a[M][M],n,m;
}a,b;
int g[M][M],nxt[M],n,m,k,ans;
char c[M];
inline void get_next(){
    for(int i=2,j=0;i<=m;++i){
        while(j&&c[i]!=c[j+1]) j=nxt[j];
        j+=(c[i]==c[j+1]);
        nxt[i]=j;
    }
    b.n=b.m=m;
    for(int i=0,l;i<m;++i){
        for(char j='0';j<='9';++j){
            l=i;
            while(l&&c[l+1]!=j) l=nxt[l];
            if(c[l+1]==j) ++b.a[i][l+1];
            else ++b.a[i][0];
        }
    }
    for(int i=0;i<b.n;++i)
        for(int j=0;j<b.m;++j)
            b.a[i][j]%=k;
}
inline matrix mul(matrix a,matrix b){
    matrix c;
    c.n=a.n;c.m=b.m;
    for(int i=0;i<c.n;++i)
        for(int j=0;j<c.m;++j){
            c.a[i][j]=0;
            for(int l=0;l<c.n;++l){
                c.a[i][j]=(c.a[i][j]+a.a[i][l]*b.a[l][j]%k)%k;
                if(b.m==1) printf("(%d,%d)=(%d,%d)*(%d,%d)\n",i,j,i,l,l,j);
            }
        }
    return c;
}
inline matrix po(matrix a,int x){
    matrix c;
    c.n=a.n;c.m=a.m;
    for(int i=0;i<c.n;++i)
        for(int j=0;j<c.m;++j)
            if(i!=j) c.a[i][j]=0;
            else c.a[i][j]=1;
    while(x){
        if(x&1){
            c=mul(c,a);
        }
        a=mul(a,a);x>>=1;
    }
    return c;
}
inline void init(){
    scanf("%d%d%d%s",&n,&m,&k,c+1);
    if(!m){
        ans=1;
        for(int i=1;i<=n;++i)
            ans=ans*10%k;
        printf("%d\n",ans);return;
    }
    get_next();
    a.n=1;a.m=m;
    a.a[0][0]=1;
    a=mul(a,po(b,n));
    for(int i=0;i<a.m;++i)
        ans=(ans+a.a[0][i])%k;
    printf("%d\n",ans);
}
int main(){
    freopen("exam.in","r",stdin);
    freopen("exam.out","w",stdout);
    init();
    fclose(stdin);
    fclose(stdout);
    return 0;
}