NOIP模拟96(多校29)

T1 子集和

解题思路

大概是一个退背包的大白板，然而我考场上想复杂了，竟然还用到了组合数。

但是大概意思是一样的，有数的最小值一定是一个在 \(a\) 数组中存在的数字。

那么我们想办法除去它对应的贡献，可以一个一个退，也可以组合数一下一起退。。。

code

#include<bits/stdc++.h>
#define int long long
#define ull unsigend long long
#define f() cout<<"RP++"<<endl
using namespace std;
inline int read()
{
	int x=0,f=1; char ch=getchar();
	while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
	return x*f;
}
const int N=1e4+10;
int n,cnt,m,top,s[N],t[N],ans[N],all[N];
inline int C(int x,int y)
{
	__int128 temp=1; int p=1;
	for(int i=y+1;i<=x;i++){temp*=i; while(p<=x-y&&temp%p==0) temp/=p,p++;}
	return (int)temp;
}
#undef int
int main()
{
	#define int long long
	freopen("subset.in","r",stdin); freopen("subset.out","w",stdout);
	n=read(); m=read();
	for(int i=0;i<=m;i++) s[i]=read();
	while(cnt<n)
	{
		int num,tot;
		for(int i=1;i<=m;i++)
			if(s[i]){num=i;tot=s[i];break;}
		for(int i=1;i<=tot;i++) ans[++cnt]=num;
		for(int i=1;i<=tot;i++) all[i]=C(tot,i),s[i*num]-=all[i];
		for(int j=num+1;j<=m;j++)
		{
			if(!s[j]) continue;
			for(int k=1;k<=tot;k++)
				s[j+num*k]-=all[k]*s[j];
		}
	}
	sort(ans+1,ans+n+1);
	for(int i=1;i<=n;i++) printf("%lld ",ans[i]);
	return 0;
}

T2 异或

解题思路

官方题解是枚举 \(k\) 的位置，然后 Tire 树计算答案，然而。。。

我的做法是对于不同的二进制位枚举 \(j\) 的位置，并计算贡献。

假设当前处理到的二进制位是 \(p\) 所有二进制位最高是 \(m\) 。

那么一对 \((i,k)\) 对于 \(j\) 有贡献，当且仅当 \(a_i,a_k\) 的 \([p+1,m]\) 这几个二进制位相同，并且如果 \(a_j\) 的这一位是 0 \(a_i\) 的这一位也是 0 \(a_k\) 的这一位也是 1 ，或者\(a_j\) 的这一位是 1 \(a_i\) 的这一位也是 1 \(a_k\) 的这一位也是 0 。

那么我们可以对于 \([p+1,m]\) 这几位出现过的数字以及 \(p\) 位上的数字开一个桶，然后直接计算贡献。

然而这样需要优化，我们可以计算每一次移动的变化值，然后记录第 \(j\) 个数字的第 \(p\) 位是 1 或者 0 的答案直接计入贡献。

具体实现开一个前缀的桶一个后缀的桶，然后可能需要离散化一下，这样会被卡常。。。

发现有些比较高的位是没有必要离散化的我们直接算就可以了，于是卡常成功！！

code

#include<bits/stdc++.h>
#define int long long
#define ull unsigend long long
#define f() cout<<"RP++"<<endl
using namespace std;
inline int read()
{
	int x=0,f=1; char ch=getchar();
	while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
	return x*f;
}
const int N=1e7+10,M=5e5+10;
int n,m,ans,cnt,lsh[N],s[M],p[M],pre[2][N],suf[2][N];
inline void solve(register int pos)
{
	register int U=((1ll<<m-pos)-1)<<pos+1,bas[2]={0,0};
	if((1ll<<m-pos)-1<=10000000)
	{
		for(register int i=1;i<=n;i++) p[i]=(s[i]&U)>>pos+1;
		for(register int i=1;i<=n;i++) pre[0][p[i]]=pre[1][p[i]]=suf[1][p[i]]=suf[0][p[i]]=0;
	}
	else
	{
		for(register int i=1;i<=n;i++) lsh[i]=(s[i]&U)>>pos+1;
		sort(lsh+1,lsh+n+1); cnt=unique(lsh+1,lsh+n+1)-lsh-1;
		for(register int i=1;i<=cnt;i++) pre[0][i]=pre[1][i]=suf[1][i]=suf[0][i]=0;
		for(register int i=1;i<=n;i++) p[i]=lower_bound(lsh+1,lsh+cnt+1,(s[i]&U)>>pos+1)-lsh;
	}
	for(register int i=1;i<=n;i++) suf[(s[i]>>pos)&1][p[i]]++;
	for(register int i=1;i<=n;i++)
	{
		register int p1=(s[i]>>pos)&1;
		suf[p1][p[i]]--; bas[p1^1]-=pre[p1^1][p[i]];
		ans+=bas[p1];
		pre[p1][p[i]]++; bas[p1]+=suf[p1^1][p[i]];
	}
}
#undef int
int main()
{
	#define int long long
	freopen("xor.in","r",stdin); freopen("xor.out","w",stdout);
	n=read(); for(int i=1;i<=n;i++) s[i]=read(),m=max(m,(int)log2(s[i]));
	for(int i=0;i<=m;i++) solve(i); printf("%lld",ans);
	return 0;
}

T3 异或 2

解题思路

此题需要高精，于是我掌握了 string 高精。。。

直接推一波柿子，其实还是比较好理解的。。

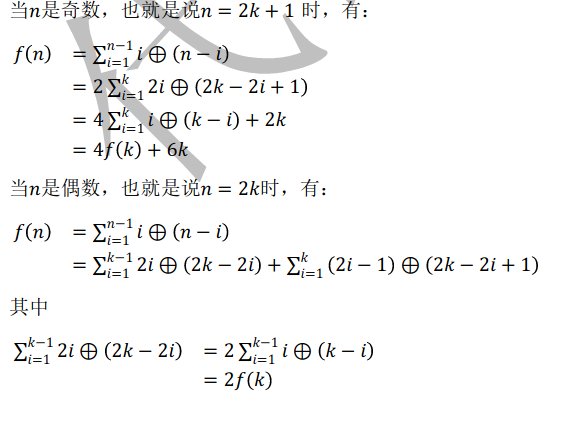
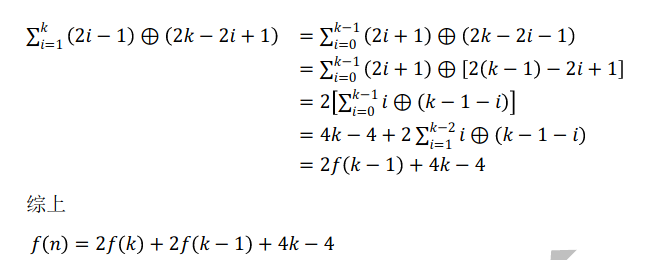
直接记忆化搜索实现即可，最多递归 log 层复杂度完全可以接受。

code

#include<bits/stdc++.h>
#define int long long
#define ull unsigend long long
#define f() cout<<"RP++"<<endl
using namespace std;
inline int read()
{
	int x=0,f=1; char ch=getchar();
	while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
	return x*f;
}
inline void write(string x){reverse(x.begin(),x.end());for(auto it:x)putchar(it+'0');putchar('\n');}
string n; map<string,string> f;
string mul(string x,int val)
{
	int lim=x.size(); string y; for(auto it:x) y.push_back(it*val); y.push_back(0);
	for(int i=0;i<y.size()-1;i++) y[i+1]+=y[i]/10,y[i]%=10; if(!(*(--y.end()))) y.pop_back();
	return y;
}
string add(string x,string y)
{
	int lim=max(x.size(),y.size())+1; string z; for(int i=1;i<=lim;i++) z.push_back(0);
	for(int i=0;i<x.size();i++) z[i]+=x[i]; for(int i=0;i<y.size();i++) z[i]+=y[i];
	for(int i=0;i<z.size()-1;i++) z[i+1]+=z[i]/10,z[i]%=10; if(!(*(--z.end()))) z.pop_back();
	return z;
}
string div(string x)
{
	for(int i=0;i<x.size();i++){if((x[i]&1)&&i) x[i-1]+=5; x[i]/=2;}
	if(!(*(--x.end()))) x.pop_back();
	return x;
}
string del(string x,int val)
{
	if(x[0]>=val) return x[0]-=val,x;
	int pos=0;
	for(int i=1;i<x.size();i++)
		if(x[i]){x[pos=i]--;break;}
	for(int i=pos-1;i>=1;i--) x[i]=9;
	x[0]=x[0]+10-val;
	return x;
}
string dfs(string x)
{
	if(f.find(x)!=f.end()) return f.find(x)->second;
	string k=div(x),temp;
	if(x[0]&1) temp=add(mul(dfs(k),4),mul(k,6));
	else temp=add(add(mul(dfs(k),2),mul(dfs(del(k,1)),2)),del(mul(x,2),4));
	return f.insert(make_pair(x,temp)),temp;
}
#undef int
int main()
{
	#define int long long
	freopen("rox.in","r",stdin); freopen("rox.out","w",stdout);
	cin>>n; reverse(n.begin(),n.end());
	for(int i=0;i<n.size();i++) n[i]-='0';
	string t1,t2; t1.clear(); t2.clear(); t1.push_back(0); t2.push_back(0); f.insert(make_pair(t1,t2));
	t1.clear(); t1.push_back(1); f.insert(make_pair(t1,t2)); t1.clear(); t1.push_back(2); f.insert(make_pair(t1,t2));
	t1.clear(); t2.clear(); t1.push_back(3); t2.push_back(6); f.insert(make_pair(t1,t2));
	write(dfs(n));
	return 0;
}

T4 卡牌游戏

解题思路

又是老脸买原题系列（虽然我没做过）

发现其实是若干个联通块，一个合法的联通块显然只能是基环树或者树，对于 -1 的情况直接并茶几根据点数边数关系判断即可。。

那么答案就是所有的联通块最小操作次数加和，方案数就是所有联通块的方案数乘积。

对于一个联通块而言，我们把牌的两边互相连边，边权分别赋值为 0 或者 1 ，那么最后的形态一定是一某个节点为根，所有的边都指向儿子。

对于树的情况直接换根 DP 即可，基环树的情况一定出现在环上的点为根的时候，直接统计。。

code

#include<bits/stdc++.h>
#define int long long
#define ull unsigend long long
#define f() cout<<"RP++"<<endl
using namespace std;
inline int read()
{
	int x=0,f=1; char ch=getchar();
	while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
	return x*f;
}
const int N=2e5+10,INF=1e18,mod=998244353;
int n,ans1,ans2=1,cnt1,cnt2,id,banx,bany,du[N],fa[N],f[N],g[N];
int tot=1,head[N],ver[N<<1],nxt[N<<1],edge[N<<1];
bool vis[N];
pair<int,int> siz[N];
void add_edge(int x,int y,int val)
{
	ver[++tot]=y; edge[tot]=val; du[y]++;
	nxt[tot]=head[x]; head[x]=tot;
}
int find(int x)
{
	if(fa[x]==x) return x;
	return fa[x]=find(fa[x]);
}
void dfs(int x,int fa)
{
	vis[x]=true;
	for(int i=head[x];i;i=nxt[i])
	{
		int to=ver[i]; if(to==fa) continue;
		if(vis[to]){id=i;banx=x;bany=to;continue;}
		dfs(to,x); f[x]+=edge[i]+f[to];
	}
}
void dfs2(int x,int fa)
{
	if(g[x]<cnt1) cnt1=g[x],cnt2=1;
	else cnt2+=g[x]==cnt1;
	for(int i=head[x];i;i=nxt[i])
		if(ver[i]!=fa&&i!=id&&(i!=(id^1)))
			if(edge[i]) g[ver[i]]=g[x]-1,dfs2(ver[i],x);
			else g[ver[i]]=g[x]+1,dfs2(ver[i],x);
}
#undef int
int main()
{
	#define int long long
	freopen("card.in","r",stdin); freopen("card.out","w",stdout);
	n=read();
	for(int i=1,x,y;i<=n;i++)
		x=read(),y=read(),
		add_edge(x,y,1),add_edge(y,x,0);
	for(int i=1;i<=2*n;i++) fa[i]=i,siz[i]=make_pair(1,du[i]);
	for(int i=1;i<=n;i++)
	{
		int x=find(ver[i<<1]),y=find(ver[i<<1|1]); if(x==y) continue;
		siz[y]=make_pair(siz[x].first+siz[y].first,siz[x].second+siz[y].second);
		fa[x]=y;
	}
	for(int i=1;i<=2*n;i++)
		if(find(i)==i&&siz[i].second>siz[i].first*2)
		printf("-1 -1"),exit(0);
	for(int i=1;i<=2*n;i++)
	{
		if(vis[i]) continue; cnt1=INF; cnt2=id=0;
		dfs(i,0); g[i]=f[i]; dfs2(i,0);
		if(!id){ans1+=cnt1;ans2=ans2*cnt2%mod;continue;}
		int t1=g[banx]+(edge[id]^1),t2=g[bany]+edge[id];
		ans1+=min(t1,t2); if(t1==t2) ans2=ans2*2%mod;
	}
	printf("%lld %lld",ans1,ans2);
	return 0;
}