洛谷 P3266 - [JLOI2015]骗我呢（容斥原理+组合数学）

题面传送门

神仙题。

首先乍一看此题非常棘手，不过注意到有一个条件 \(0\le x_{i,j}\le m\)，而整个矩阵恰好有 \(m\) 列，这就启发我们考虑将每个元素的上下界求出来，如果我们第一列全填 \(0\)，其余每个数都恰好等于它左边的数加 \(1\)，那么 \(x_{i,j}\) 刚好取到下界 \(j-1\)；如果我们最后一列全填 \(m\)，其余每个数都恰好等于它右边的数减 \(1\)，那么 \(x_{i,j}\) 刚好取到上界 \(j\)，因此对于任意一个第 \(j\) 列的元素 \(x_{i,j}\)，它的取值只有两种：\(j-1\) 和 \(j\)。

我们记一类格为填 \(j-1\) 的 \(x_{i,j}\)，二类格为填 \(j\) 的 \(x_{i,j}\)，那么不难发现对于一个二类格 \(x_{i,j}\)，所有形如 \(x_{i-p,j+q}\)，\(p\le q\) 的格子（也就是下图中的蓝色区域）都必须是二类格，而不难发现对于任意一个合法的矩阵，都存在唯一的二类格的集合 \(S\)，满足任意两个二类格都不在互相所管辖的范围内。因此题目可以转化为，有多少个二类格的集合 \(S\)，满足任意两个格子都不在互相管辖的范围内。

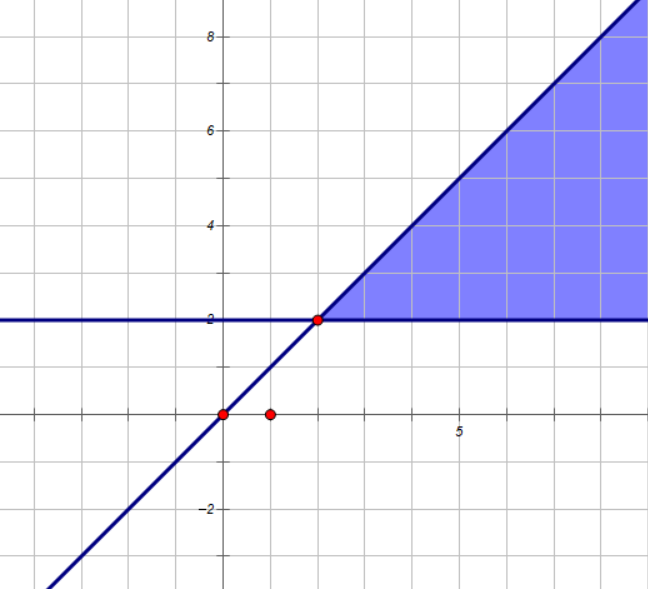
考虑 \(dp\)，不难发现任意一行，一类格必定是一段后缀，因此记 \(dp_{i,j}\) 表示从下往上考虑到了第 \(i\) 行，一类格前缀长度为 \(j\) 的方案数，那么显然上一行一类格前缀的长度 \(\le j+1\)，因此我们不难得到 \(dp\) 转移方程式 \(dp_{i,j}=\sum\limits_{k=j-1}^{m}dp_{i+1,k}\)，上式稍微化简一下可以得到 \(dp_{i,j}=dp_{i,j+1}+dp_{i+1,j-1}\)，注意，对于 \(dp_{i,m}\) 而言，上式只有 \(dp_{i+1,m-1}\)，而实际上 \(dp_{i+1,m}\) 也能转移到 \(dp_{i,m}\)，故 \(dp_{i,m}=dp_{i+1,m-1}+dp_{i+1,m}\)。

这样 \(dp\) 是 \(nm\) 的，无法通过，考虑使用组合意义优化，对于 \(n=3,m=3\) 而言，该 \(dp\) 的值等价于下图（这里借用了张题解区的图）中从左上角走到右下角的方案数（提示：如果将整张图旋转 \(\pi\) 那可能比较好理解，因为上面的 \(dp\) 过程是从下往上推的）

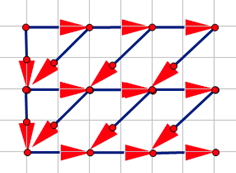
稍微将它变形一下可以得到下图：

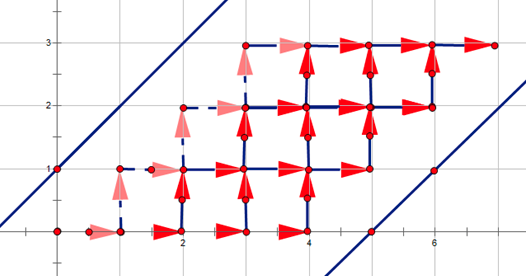
不难发现这东西就等价于从 \((0,0)\) 出发到达 \(P(n+m+1,n)\) 的方案数，其中不能碰到直线 \(A:y=x+1\) 和直线 \(B:y=x-(m+2)\)

这个东西怎么求呢？一个比较棘手的地方是它涉及两条直线，如果只涉及一条直线那可以像我们的经典问题——求卡特兰数递推式那样做一个对称然后简单求个组合数。因此这里介绍一种思考问题的方法：前缀容斥。注意到对于所有不合法情况，它经过直线 \(AB\) 的情况必然构成一个序列，比方说 \(AABBAABBBA\)，把连续段缩一下可以得到 \(ABABA\)，我们不妨就从这个缩好的序列入手计算方案数。显然对于每个不合法的序列，它缩好的序列要么以 \(A\) 开头要么以 \(B\) 开头，因此答案就是总方案数减去以 \(A\) 开头的方案数减去以 \(B\) 开头的方案数。

怎样求以 \(A\) 开头的方案数呢？我们不妨把以 \(A\) 开头的方案罗列一下，可以得到：

• A
• AB
• ABA
• ABAB
• ...

看到以 \(A\) 开头我们直观地想到做 \(P(n+m+1,n)\) 关于直线 \(A\) 的对称点 \(P'\)，但事实上这是不对的。In fact，仔细分析一下就可以发现，对于所有 \((0,0)\) 到 \(P'\) 的路径，如果我们把最后一个与 \(A\) 的交点 \(X\) 找到，然后把 \(X\to P'\) 的折线翻下来，那么最后一段 \(X\to P'\) 必然与 \(A\) 没有交点，因此这样的路径末尾要么是 \(A\)（最后一段与 \(B\) 没有交点）要么是 \(AB\)（最后一段与 \(AB\) 有交点），因此求得的方案数是以 \(A\) 或 \(AB\) 为结尾的方案数，但这样只是以 \(A\) 或 \(AB\) 结尾的啊，还会多算什么 \(BA,BAB,ABA,ABAB\cdots\)，别急，如果我们再作 \(P'\) 关于 \(B\) 的对称点 \(P''\)，那么所有 \((0,0)\to P''\) 的路径必然经过 \(B\)，再把它翻上来就得到了 \((0,0)\to P'\) 的路径，由已知 \((0,0)\to P'\) 所对应的 \((0,0)\to P\) 的路径要么以 \(A\) 为结尾，要么以 \(AB\) 为结尾，前面再填个 \(B\)，故 \((0,0)\to P''\) 所对应的路径要么以 \(BA\) 为结尾，要么以 \(BAB\) 结尾，发现就是上面 \(BA,BAB,ABA,ABAB\cdots\)，二者相减就得到了 \(A,AB\) 的方案数。

求 \(ABA,ABAB\)，以及后面 \(ABABA,ABABAB\cdots\) 的方案数也同理，只需要再做 \(P''\) 关于 \(A\) 的对称点计算方案数，再关于 \(B\) 对称计算方案数，二者相减即可得到 \(ABA,ABAB\) 的方案数，以此类推即可求出以 \(A\) 开头的方案数。求以 \(B\) 开头的也同理。

时间复杂度 \(\mathcal O(n)\)

const int MAXN=6e6+4;
const int MOD=1e9+7;
int n,m,fac[MAXN+5],ifac[MAXN+5];
void init_fac(int n){
	for(int i=(fac[0]=ifac[0]=ifac[1]=1)+1;i<=n;i++) ifac[i]=1ll*ifac[MOD%i]*(MOD-MOD/i)%MOD;
	for(int i=1;i<=n;i++) fac[i]=1ll*fac[i-1]*i%MOD,ifac[i]=1ll*ifac[i-1]*ifac[i]%MOD;
}
int binom(int x,int y){return 1ll*fac[x]*ifac[y]%MOD*ifac[x-y]%MOD;}
void flip(int &x,int &y,int a){x^=y^=x^=y;x-=a;y+=a;}
int ways(int x,int y){return (x<0||y<0)?0:binom(x+y,x);}
int main(){
	scanf("%d%d",&n,&m);init_fac(MAXN);
	int x=n+m+1,y=n,ans=ways(x,y);
	while(x>=0&&y>=0){
		flip(x,y,1);ans=(ans-ways(x,y)+MOD)%MOD;
		flip(x,y,-m-2);ans=(ans+ways(x,y))%MOD;
	} x=n+m+1,y=n;
	while(x>=0&&y>=0){
		flip(x,y,-m-2);ans=(ans-ways(x,y)+MOD)%MOD;
		flip(x,y,1);ans=(ans+ways(x,y))%MOD;
	} printf("%d\n",ans);
	return 0;
}