题解 [NOIP2017 提高组]宝藏

传送门

这是蓝书上状压的例题啊，怎么会出现在模拟赛里

不过就算原题我也没把握写对

核心思路：

先令\(dp[s]\)为当前状态为\(s\)时的总花费最小值，\(cnt[s][i]\)为这个方案中由根节点（赞助商打通的节点）到\(i\)节点最少经过的房间数

此题转移较为麻烦，转移时需要知道当前每个点经过了几个房间

考虑对每个状态开个数组记录到此状态每个点经过了几个房间

注意这个\(cnt\)数组是\(dp\)值的附属物，所以\(dp\)值更新的时候\(cnt[]\)需要跟着覆写过去

然后就是一个状压求最小值的板子了

怎么可能这么简单，这里的转移覆写的后效性怎么说？

然而事实是，这里每次转移取最小值更新根本没有后效性

所以考场上直接猜个结论开始写可以有100pts拿 （弥天大雾

好了这个后效性的有无是此题难点

因为如果真的有后效性的话我们并不知道如何消除它，所以我们试着去证明这里不必处理后效性，杀敌于无形之中

首先考虑我们所说这里的后效性是什么：

放张图：

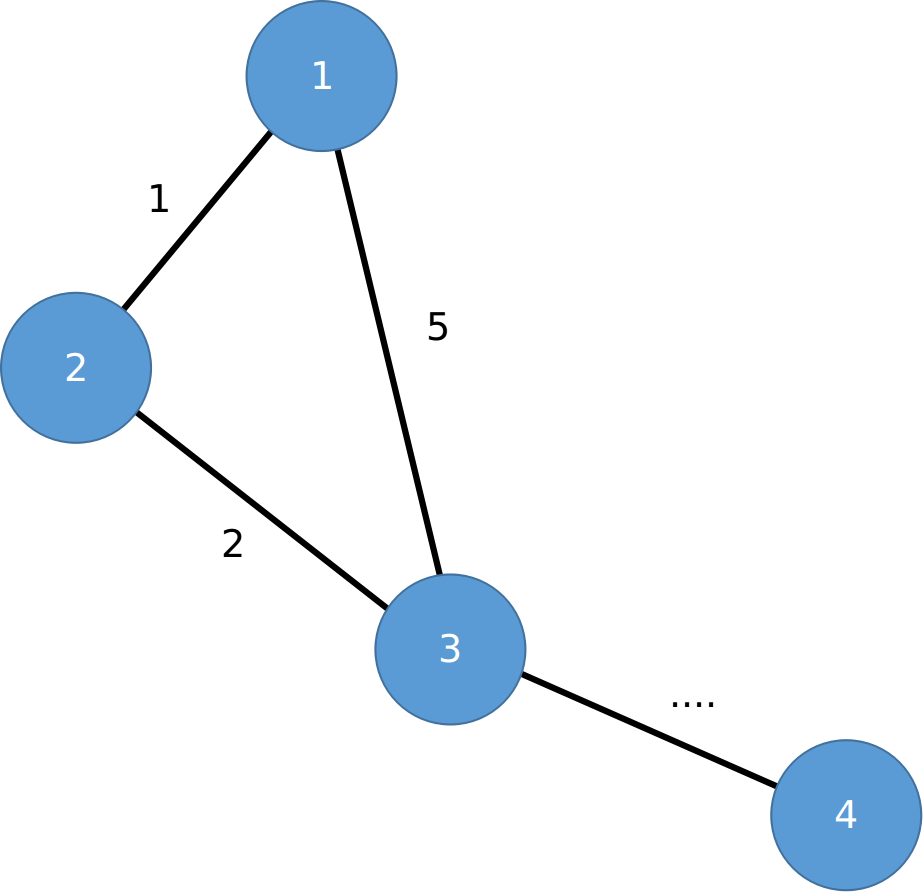
令赞助商打通的是节点1

那么对于这个节点3，它会被1-2-3这条路径更新，\(cnt=3\)

而1-3这条路径虽然权值更大，但其\(cnt=2\)

对于后续的更新无法判断谁更优，

那这里直接由1-2-3把3更新掉不就有后效性了吗？

然而我们更新3的实质是\(dp[0111] = min(dp[0011], dp[0101])\)

我们所想象的后效性是在节点1，2，3均打通后向4转移会有后效性

谁说我们一定要先打通1，2，3才能向4转移了？

考虑节点4的更新，\(dp[1111] = min(dp[0111], dp[1101])\)（其它状态不合法，已舍去）

由方程知这里可以也考虑了1-3-4-2的方案，推广到所有情况，会考虑少一条边的所有可能，并没有后效性

同样由方程知，我们在状压时实际考虑了所有点向这个点所有可能的连边方案，

而我们所想的「后效性」，实质上是「在已固定了几条连边后出现的后效性」

则我们直接列出方程

\[dp[s|(1<<v)] = min(dp[s|(1<<v)], dp[s]+edge.val*cnt[s][i])
\]

而这里的cnt数组是dp值的附属物，在转移的同时要把\(cnt[s]\)覆写过去

然后按方程转移即可

哦对了还有这个题里全是重边，建议开邻接矩阵存边

Code:

#include <bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
#define ll long long
#define ld long double
#define usd unsigned
#define ull unsigned long long
//#define int long long 

#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf, 1, 1<<21, stdin)), p1==p2?EOF:*p1++)
char buf[1<<21], *p1=buf, *p2=buf;
inline int read() {
	int ans=0, f=1; char c=getchar();
	while (!isdigit(c)) {if (c=='-') f=-f; c=getchar();}
	while (isdigit(c)) {ans=(ans<<3)+(ans<<1)+(c^48); c=getchar();}
	return ans*f;
}

int n, m;
ll dp2[13][1<<14], val[15];
int cnt[13][1<<14][13];
int head[20], size;
int mp[15][15];
inline void add(int s, int t, int w) {mp[s][t]=min(mp[s][t], w); mp[t][s]=min(mp[t][s], w);}

signed main()
{
	#ifdef DEBUG
	freopen("1.in", "r", stdin);
	#endif
	memset(dp2, 127, sizeof(dp2));
	memset(mp, 127, sizeof(mp));

	n=read(); m=read();
	int lim=1<<n;
	for (int i=1,u,v,w; i<=m; ++i) {u=read(); v=read(); w=read(); add(u, v, w); add(v, u, w);}
	for (int begin=0; begin<n; ++begin) {
		dp2[begin][1<<begin] = 0;
		cnt[begin][1<<begin][begin] = 1;
		ll *dp=dp2[begin];

		for (int s=1; s<lim; ++s) {
			for (int j=0; j<n; ++j) {
				if (!(s&(1<<j))) continue;
				for (int i=1,v; i<=n; ++i) {
					if (j+1==i || mp[j+1][i]>500010) continue;
					v = i-1;
					if (s&(1<<v)) continue;

					if (dp[s]+1ll*mp[j+1][i]*(cnt[begin][s][j]) < dp[s|(1<<v)]) {
						dp[s|(1<<v)] = min(dp[s|(1<<v)], dp[s]+1ll*mp[j+1][i]*(cnt[begin][s][j]));
						for (int k=0; k<n; ++k) cnt[begin][s|(1<<v)][k] = cnt[begin][s][k];
						cnt[begin][s|(1<<v)][v] = cnt[begin][s][j]+1;
					}
				}
			}
		}
	}
	ll ans=INF;
	for (int i=0; i<n; ++i) ans = min(ans, dp2[i][lim-1]);
	printf("%lld\n", ans);

	return 0;
}