noip 模拟9 题解

rp++==文化课报废

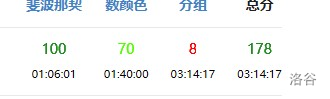
考试经过

先看T1，有被1e12吓到，但根据经验这很可能是水题，经过一番观察后直接打表，似乎看出了规律，觉得应该有了正解，写完之后顺利过掉大样例，但似乎时间稍慢一点，写上快读交了一遍，觉得应该没问题

T2看一眼就是数据结构题，先冲上30分暴力，觉得建3e5个树状数组不太现实，分块又不太会，认为动态开点线段树可做，凭借我80余次万紫千红的经验顺利打完，一遍就过了大样例，觉得稳了，交了

T3毒瘤题面，读题半小时毫无头绪。。。利用特判大法水到8分，由于不知道字典序最小怎么办，又懒得写爆搜，就拿指针乱扫，没过样例，嘎，然后我就没有梦想了，1h毫无进展，最后检查了一遍代码提交

100+70+8=178，T3完全废掉，又水成rank1了

T1.斐波那契

看那个图标出来了每一代都有谁，我们发现好像一代兔子的父亲都是递增的，理所当然的打表，可以发现对于每只兔子x，他的父亲是 $ x-fib_i $ ,fib[i]是不大于x的最大的斐波那契数，只用斐波那契前60项就够，所以我们在60以内就找到了父亲，那么一直跳就行了，这里我们只对编号大的跳父亲，一直递归就能出解。最优复杂度是O60n，我可能稍微慢一点qwq

#include <bits/stdc++.h>
using namespace std;
#define int long long
inline int read()
{
	int x=0,f=1; char ch=getchar();
	while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
	while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
	return x*f;
}
int a[65];
inline int getf(int x)
{
	int i=1;
	for(;i<=60;i++)
	 if(a[i]>=x)return a[i-1];
}
inline int get(int x,int y)
{
	if(x==y)return x;
	if(x<y)swap(x,y);
	x=x-getf(x);
	return get(x,y);
}
signed main()
{
//      freopen("sb.txt","r",stdin);
//      freopen("a.out","w",stdout);
	a[0]=0;a[1]=1;a[2]=1;
        for(int i=3;i<=63;i++)a[i]=a[i-1]+a[i-2];
	int m;m=read();
	for(int i=1;i<=m;i++)
	{
		int x,y;
        x=read();y=read();
        printf("%lld\n",get(x,y));
	}
//	fclose(stdin);
//	fclose(stdout);
	return 0;
}

T2.数颜色

对每个颜色动态开店建线段树，单点修改区间查询，oj慢所以开始没A，不用longlong，数组稍微大点

#include <bits/stdc++.h>
using namespace std;
const int N=300050;
inline int read()
{
	int x=0,f=1; char ch=getchar();
	while(ch<'0'||ch>'9'){ if(ch=='-') f=-1; ch=getchar(); }
	while(ch>='0'&&ch<='9'){ x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); }
	return x*f;
}
int ls[80*N],rs[80*N],sum[80*N],num;
int add(int x,int l,int r,int p,int v)
{
	if(!x)x=++num;
	if(l==r)
	{
		sum[x]+=v;
		return x;
	}
	int mid=(l+r)>>1;
	if(p<=mid)ls[x]=add(ls[x],l,mid,p,v);
	if(p>mid)rs[x]=add(rs[x],mid+1,r,p,v);
	sum[x]=sum[ls[x]]+sum[rs[x]];
	return x;
}
int getsum(int x,int l,int r,int pl,int pr)
{
	if(!x)return 0;
	if(pl<=l&&pr>=r)return sum[x];
	int mid=(l+r)>>1;
	if(pr<=mid)return getsum(ls[x],l,mid,pl,pr);
	if(pl>mid)return getsum(rs[x],mid+1,r,pl,pr);
	return getsum(ls[x],l,mid,pl,pr)+getsum(rs[x],mid+1,r,pl,pr);
}
int mp[N],b[N];
signed main()
{
//    freopen("sb.txt","r",stdin);
//    freopen("a.out","w",stdout);
	int n,m;n=read();m=read();
	for(int i=1;i<=n;i++)
	{
		int c;c=read();
		if(!mp[c])mp[c]=++num;
		add(mp[c],1,N,i,1);b[i]=c;
	}
	for(int i=1;i<=m;i++)
	{
		int op;op=read();
		if(op==1)
		{
			int l,r,c;l=read();r=read();c=read();
			printf("%d\n",getsum(mp[c],1,N,l,r));
		}
		if(op==2)
		{
			int x;x=read();
			add(mp[b[x]],1,N,x,-1);
			add(mp[b[x]],1,N,x+1,1);
			add(mp[b[x+1]],1,N,x+1,-1);
			add(mp[b[x+1]],1,N,x,1);
			swap(b[x],b[x+1]);
		}
	}
//	fclose(stdin);
//	fclose(stdout);
	return 0;
}

其实还可以排序+二分，懒得写了就挂上战神的博客吧

T3.分组

首先这个题有若干种骗分技巧

解决字典序最小的方法就是从后往前枚举你说你T1T2都出正解了连这都想不到

那么K=1就很简单了，从后往前扫一遍就行，每次判断是否有冲突，有了就累计答案清空数组

判断的时候直接枚举定T飞，注意到131072=512*512，所以每次只要枚举x<=512,x^2-a[i]是否出现即可，40到手

对于K=2，还是从后往前分组，判定的时候相当于判定二分图，O3暴力到80虽然本蒟蒻没学过神马是二分图

正解其实是并查集，类比1e9年前做过的关押罪犯，使用扩展域的并查集判断，每次判断，处理，合并

一旦碰到冲突的就合并，然后判断是不是已经在一个集合内，如果已经重了，有两种情况：如果这个数2倍是完全平方数并且出现恰好2次，前面的数没有和他冲突的，那么没事；否则就要重新分段

这个特判的本质就是在一堆不合法情况里面把合法的排出来，细节有点多

#include <bits/stdc++.h>
using namespace std;
int a[300005];int mem[300005];
stack <int> s;
int ans[300005],num;
inline void add(int x){ans[++num]=x;}
int f[300005];int n,k;
inline int find(int x)
{
	if(f[x]!=x)f[x]=find(f[x]);
	return f[x];
}
inline void tu(int x,int y)//y合并到x上
{
	x=find(x);y=find(y);
	f[y]=x;
}
inline void clear()
{
	while(!s.empty())
	{
		if(k==2)f[s.top()]=s.top();
		if(k==2)f[s.top()+131072]=s.top()+131072;
	    mem[s.top()]=0;
		s.pop();
	}
}
bool gan(int x)
{
	for(int j=ceil(sqrt(x));j<=512;j++)
	{
		if(mem[j*j-x]&&((j*j-x)!=x))return 0;
	}
	return 1;
}
signed main()
{
//	freopen("sb.txt","r",stdin);
	cin>>n>>k;
	for(int i=1;i<=n;i++)scanf("%d",&a[i]);
	int an=1;
	if(k==1)
	{
		for(int i=n;i>=1;i--)
	    {
		   for(int j=ceil(sqrt(a[i]));j<=512;j++)//注意合法，j*j>=a[i]
		   if(mem[j*j-a[i]])
		   {
		 	 an++;add(i);clear();
		 	 break;
		   }
		   mem[a[i]]++;s.push(a[i]);
	    }
	}
	if(k==2)
	{
		for(int i=1;i<=300000;i++)f[i]=i;
		for(int i=n;i>=1;i--)
		{
		   s.push(a[i]);
		   for(int j=ceil(sqrt(a[i]));j<=512;j++)
		   {
		   	int p=j*j-a[i];
		   	if(!mem[p])continue;
            tu(p+131072,a[i]),tu(p,a[i]+131072);
		   	if(find(a[i])==find(a[i]+131072))
		   	{
				if(a[i]==p&&gan(a[i])&&mem[p]==1)continue;
				an++;add(i);clear();break;
		    }
		   }
	       mem[a[i]]++;s.push(a[i]);
		}
	}
	printf("%d\n",an);
    for(int i=num;i>=1;i--)printf("%d ",ans[i]);
	return 0;
}

清空数组我用的栈，可以省时间，但一定要清干净，也可以用memset，就是慢点，可能会T1个点

考试总结

1.脑子要清晰

2.不能大意，不要以为做出来一两道就行了,发挥出最好水平