MATLAB—面向复数和数组的基本运算

文章目录

• 一.MATLAB基本运算说明
• 二.面向复数的计算特点
• • 1.基础知识
  • 2.对复数的基本操作
  • 3.复数的开方问题
• 二.面向数组
• • 1.数组的输入形式
  • 2.对矩阵中的元素进行并行操作
  • 3.利用数组运算，实现函数可视化
  • 4.实现矩阵之间的点乘

一.MATLAB基本运算说明

MATLAB的基本运算符如示：

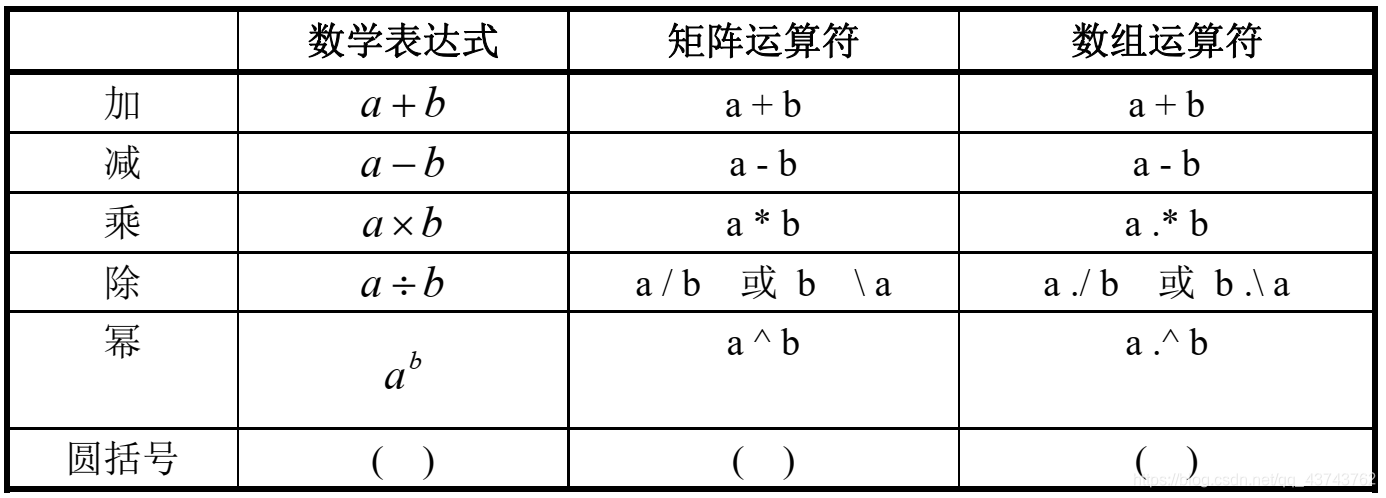
求e的x次方：exp(x)

• MATLAB面向复数设计，其所有运算都定义在复数域上，所以对于方根运算，运算只返回一个“主解”，所以要得到复数的全部方根，必须编写专门程序。
• MATLAB面向矩阵/数组设计，所以标量都被看作（1X1）的矩阵/数组。
• 数组运算的“乘、除、幂”规则与相应矩阵运算根本不同。前者的算符比后者多一个“小
  黑点”。
• MATLAB 用左斜杠或右斜杠分别表示“左除”或“右除”运算。对标量而言，“左除”
  和“右除”的作用结果相同。但对矩阵来说，“左除”和“右除”将产生不同的结果。

二.面向复数的计算特点

1.基础知识

MATLAB 的所有运算都是定义在复数域上的。这样设计的好处是：在进行运算时，不
必像其他程序语言那样把实部、虚部分开处理。为描述复数，虚数单位用预定义变量 i 或 j
表示。
所以，变量i j都是预定义变量，不可以再被赋值：

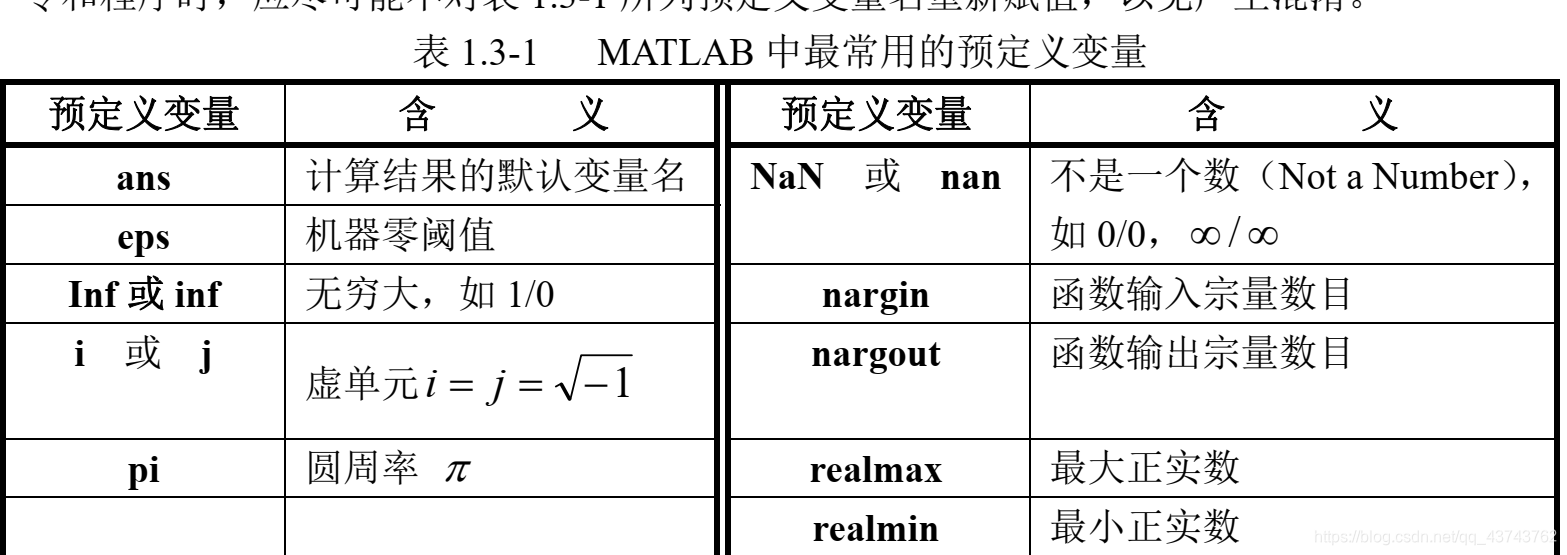
2.对复数的基本操作

所以，既然运算都是定义在复数上的，就衍生出了对复数操作的函数：

将辐角转换为以°为单位：angle(z)*180/pi

3.复数的开方问题

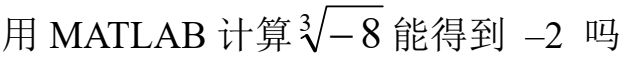
分三种方法实现，看看哪种才是准确的

1.先试着直接计算x=(-8)^(1/3)
得出结果如下：

显然不是我们预期的结果！！！得到的只是处于第一象限的方根！！！

2.利用解多项式的方法求出
构建多项式x^3-(-8)，然后通过解多项式来得到(-8)^(1/3)的全部解（基于复数域）

可以得出基于复数域的全部解，第一个解-2.0000 + 0.0000i就是实数解-2。
解释一下如何构建多项式以及如何得到多项式的根：

MATLAB表示多项式为包含由下降幂排列的系数的行向量。 例如，方程式:
P(x)=4x³-5x²+3x-7
MATLAB中：p=[4,-5,3,-7]
再通过：x=roots( p )就可以得出多项式的根
根会以数组的形式存储在变量x中

3.通过图形表示
基于求解多项式根的前提，将三个解在坐标中表示出来

二.面向数组

在MATLAB中，标量数据被看作1X1的数组数据，所有的数据都存放在适当大小的数组中。为了加快计算速度，MATLAB对以数组形式存储的数据设计了俩种基本运算：

• 数组运算
• 矩阵运算

1.数组的输入形式

2.对矩阵中的元素进行并行操作

3.利用数组运算，实现函数可视化

最终得出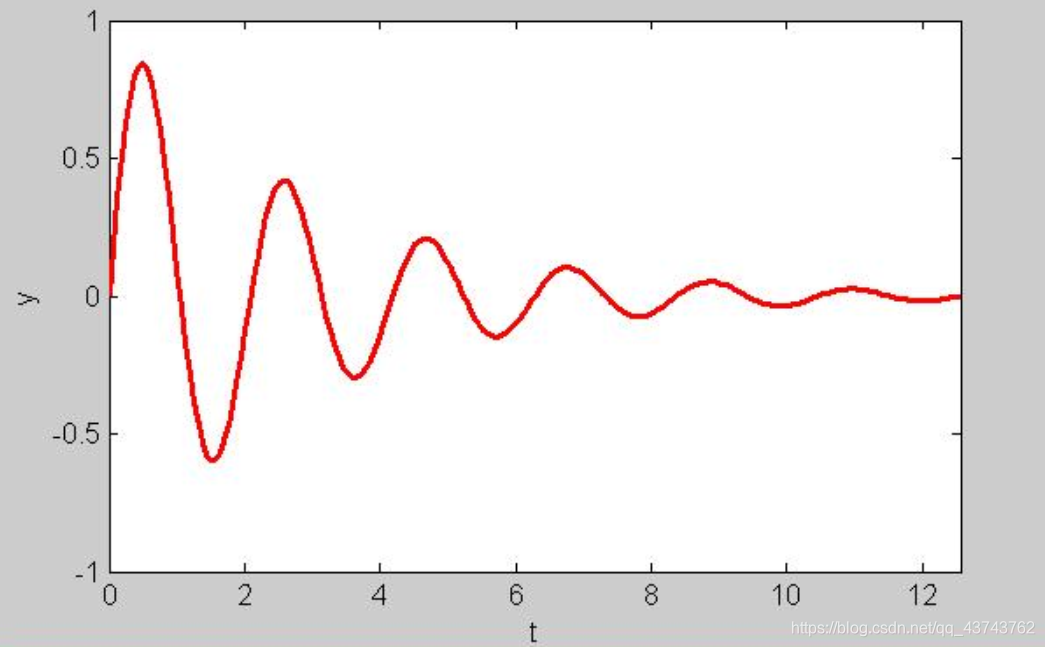
需要注意的有：

• t=0:pi/50:4*pi相当于创建了一个数组，数组范围为从0到4*pi，元素间距为pi/50。
• y=exp(-t/3).*sin(3*t)中“.*”符号表示：乘法是在俩个数组相同位置上的元素间进行的，这样才可以做到t于y的一一对应。

4.实现矩阵之间的点乘