Linux账号和权限管理（第二回合）

一.组账号文件
二.添加组账号groupadd
三.添加删除组成员gpasswd
四.删除组账号groupdel
五.查询账号信息finger
六.文件/目录的权限和归属
七.设置文件和目录的归属chown

一.组账号文件

① 与用户账号文件相类似

• /etc/group：保存组账号基本信息

• /etc/gshadow：保存组账号的密码信息

② 表现形式

字段1: 组账号的名称

字段2: 占位符“x”

字段3: 组账号的GID号

字段4: 组账号包含的用户成员(一般不包括基本组对应的用户帐号)，多个成员之间以逗号“，”分隔

二.添加组账号groupadd
① groupadd命令
groupadd 【-g GID】组账号名

② 举例

三.添加删除组成员gpasswd

① gpasswd命令

设置组账号密码（极少用）、添加/删除组成员

gpasswd 【选项】 组账号名

② 常用选项

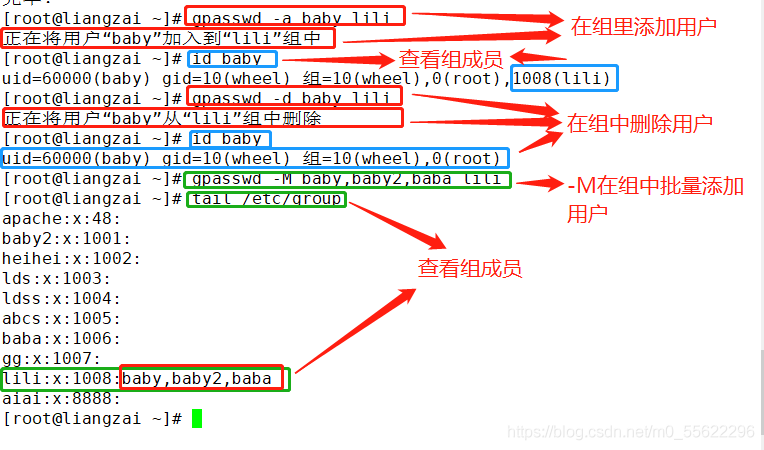
-a：向组内添加一个用户

-d：从组内删除一个用户成员

-M：定义组成员列表，以逗号分割

③ 举例

四.删除组账号groupdel

① groupdel命令

groupdel 组账号名

② 举例

五.查询账号信息finger
① finger命令
查询用户账号的登录属性
注：需要先进行安装finger软件包

finger 【用户名】

② w、who、users命令
查询已登录到主机的用户信息

通常使用tty来简称各种类型的终端设备，Centos7 系统，tty1表示图形界面，tty2-tty6表示文字界面，可以用Ctrl+Alt+F1-F6切换

按Ctrl+A1t+F2登陆，执行w命令，查看使用的终端就是tty2

pts说明是用远程工具连接的，比如xshell,后面的数字代表登录的时间顺序，越小证明登录的越早

③ 举例
finger:

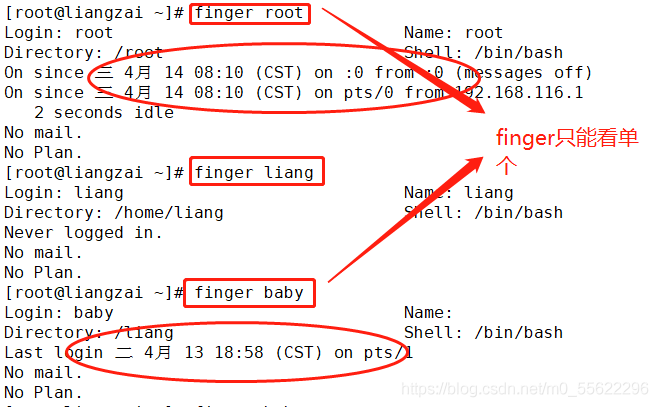
w who users:

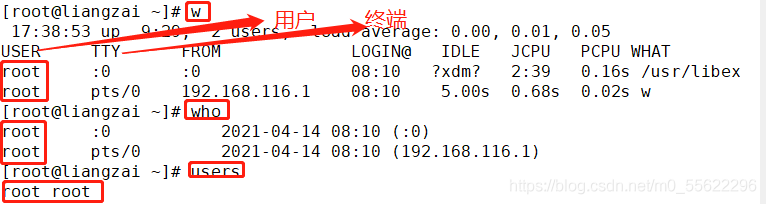
六.文件/目录的权限和归属
① 访问权限
读取r: 允许查看文件内容、显示目录列表

写入w: 允许修改文件内容，允许在目录中新建、移动、删除文件或子目录

可执行x: 允许运行程序、切换目录

② 归属（所有权）
属主: 拥有该文件或目录的用户帐号

属组: 拥有该文件或目录的组帐号

查看文件/目录的权限和归属

设置文件/目录的权限chmod
① chmod 命令
chmod 【ugoa】【+ - =】 【rwx】文件或目录

chmod nnn（3位八进制数） 文件或目录

• "ugoa"表示该权限设置所针对的用户类别。“u”代表文件属主，“g”代表 文件属组内的用户，“o”代表其他任何用户，“a"代表所有用户(缺省时为a)

• “+ - ="表示设置权限的操作动作。“+"代表增加相应权限，“-"代表减少相应权限，“=”代表仅设置对应的权限

• “rwx”是权限的字符组合形式，也可以拆分使用，如“r”"rx” 等

举例

②chmod + nnn（3位八进制数）+ 文件或目录：

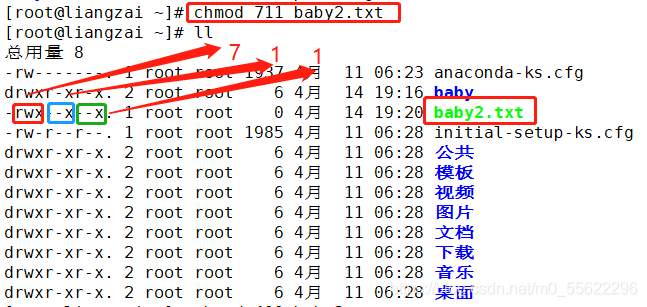
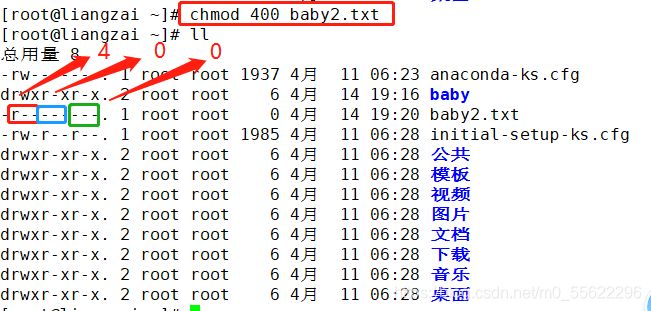
七.设置文件和目录的归属chown
① chown 命令
chown 属主 文件或目录

chown : 属组 文件或目录.
chgrp 属组 文件或目录

chown 属主:属组 文件或目录
chown 属主.属组 文件或目录

②常用选项
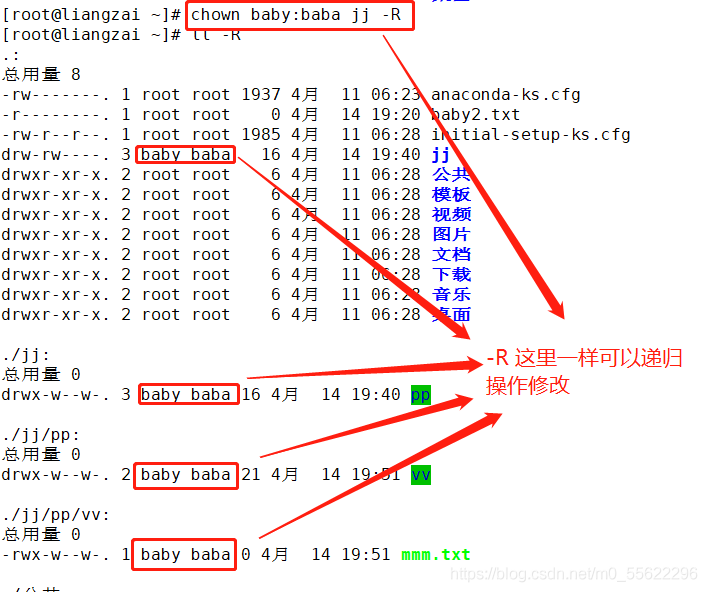
-R:递归修改指定目录下所有文件、子目录的归属

③ 举例
chown 属主 文件或目录：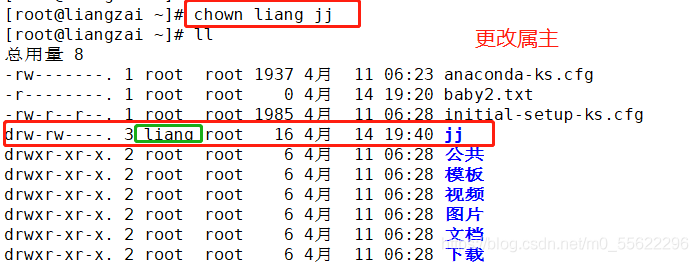

chown : 属组 文件或目录：

chgrp 属组 文件或目录：

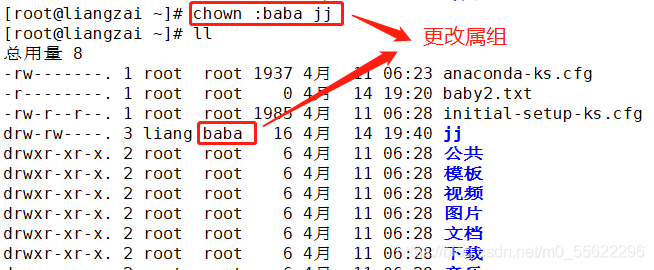
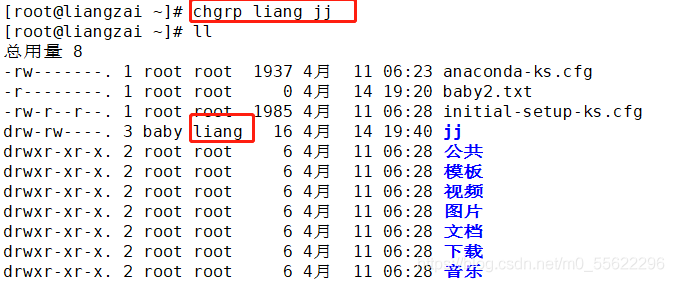
chown 属主:属组 文件或目录：

总结
用户账号管理 (useradd、 passwd、 usermod、 userdel)

组账号管理 (groupadd、gpasswd、 groupdel)

用户账号文件与组账号文件

查询账号相关信息的命令 (groups、id、finger, w)

设置目录与文件权限 (chmod)

设置目录与文件归属 (chown)