跳表--怎么让一个有序链表能够进行"二分"查找?

对于一个有序数组，如果要查找其中的一个数，我们可以使用二分查找(Binary Search)算法，将它的时间复杂度降低为O(logn).那查找一个有序链表，有没有办法将其时间复杂度也降低为O(logn)呢？

跳表(skip list),全称为跳跃链表，实质上就是一种可以进行二分查找的有序链表，它允许快速查询、插入和删除有序链表。

跳表使用的前提是链表有序，就像二分查找也要求有序数组

怎么理解跳表

比如我们有一个原始有序链表，如下图所示。

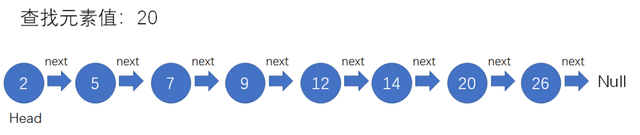
要查找其中值为20的元素，之前都是采取按顺序进行遍历的方法，但这样做时间复杂度就变成了O(n).怎样才能提高效率呢？我们可以通过对链表建立一级索引，查找的时候先遍历索引，通过索引找到原始层继续遍历。索引如下图所示

那么查找20的过程就变成了先使用索引遍历 2 -> 7 -> 12 -> 20，然后顺着索引链表的结点向下找到原始链表的结点20.之前需要遍历7次，现在需要遍历5次。在数据量小的时候跳表性能优化并不明显，但当有序链表包含大量数据时，结点的访问次数大致会减少一半。

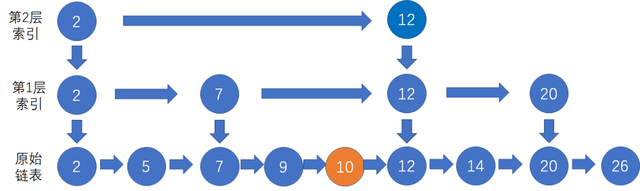
现在我们添加两层索引，基于第一层的索引再添加一层，如下图所示

要查找20，先在第二层索引上遍历 2 -> 12 ,然后向下转到第一层索引遍历 12 - > 20，最后向下找到原始链表的结点20.

这个例子中，原始有序链表的结点数量很少，当结点数量很多时，可以抽出更多的索引层级，每一层索引结点的数量都是低层索引的一半。

跳表复杂度分析

时间复杂度

算法的执行效率可以通过时间复杂度来衡量，跳表的时间复杂度是多少呢？我们来分析一下。

前面我们每两个结点抽一个结点作为上一级索引的结点，那么假设原始链表的长度为n，第一层索引的结点个数为n/2,第二层索引的个数为n/4,第k级的索引结点个数就是n/(2^k)。假设索引有 h 级，最高级的索引有 2 个结点。通过上面的公式，我们可以得到 n/(2^h)=2，从而求得 h=log₂n-1。如果包含原始链表这一层，整个跳表的高度就是 log₂n。我们在跳表中查询某个数据的时候，如果每一层都要遍历 m 个结点，那在跳表中查询一个数据的时间复杂度就是 O(m*logn)。

m的值怎么计算呢？在上面的例子中，每一层最多只需要遍历三个元素，因此m=3，根据时间复杂度的计算规则，高阶的常数项也可以省略，因此跳表中查询任意数据的时间复杂度就是O(logn)

空间复杂度

每两个结点中抽一个结点作为上级索引，很明显，它的空间复杂度为O(n).

‍♂这是一个典型的空间换时间操作。原始链表中存储的有可能是很大的对象，而索引结点只需要存储关键值和几个指针，并不需要存储对象，所以当对象比索引结点大很多时，索引占用的额外空间就可以忽略了。

高效的插入和删除

插入操作

向链表插入数据的时间复杂度是O(1),但为了保持链表数据有序，需要先找到插入结点的前置结点，然后插入数据到前置结点后面，其时间复杂度为O(logn)。假设我们要插入10，需要先找到前置结点9，然后插入10。

删除操作

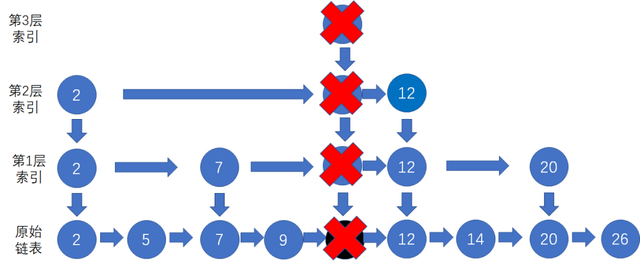
删除的话也是需要先找到要删除的结点，如果该结点在索引中也有出现的话，索引中的也需要删除。因为单链表中的删除操作需要拿到要删除结点的前驱结点，然后通过指针操作完成删除。所以在查找要删除的结点的时候，一定要获取前驱结点。

动态更新索引

当我们一直往跳表中插入数据时，两个索引结点之间的数据可能会变得非常多，在极端情况下，跳表还会退化成单链表，这样的话跳表的优势也就没有了。

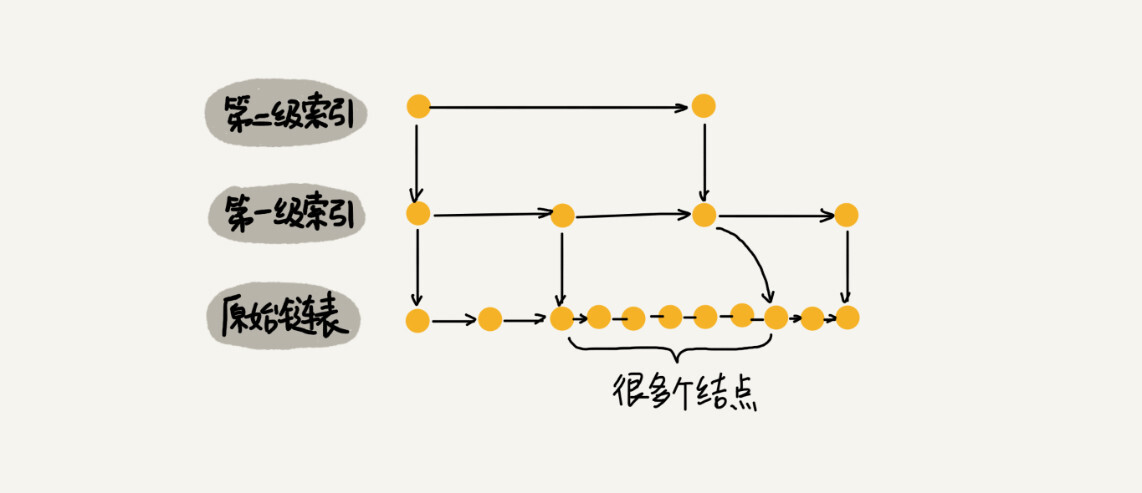
因此我们需要用一些方法来维护索引和原始链表之间的平衡，也就是在增加原始链表中结点内容的时候适当增加索引的大小。为了维护平衡，跳表的设计者采用了一种有趣的方法：“抛硬币”，也就是随机决定新结点是否建立索引，两个结点建立一个索引的话，每层的概率为50%。

Java实现跳表

下面是王争老师 数据结构与算法之美 课程中的代码

package skiplist;
/**
 * 跳表的一种实现方法。
 * 跳表中存储的是正整数，并且存储的是不重复的。
 *
 * Author：ZHENG
 */
public class SkipList {
  private static final float SKIPLIST_P = 0.5f;
  private static final int MAX_LEVEL = 16;
​
  private int levelCount = 1;
​
  private Node head = new Node();  // 带头链表
​
  public Node find(int value) {
    Node p = head;
    for (int i = levelCount - 1; i >= 0; --i) {
      while (p.forwards[i] != null && p.forwards[i].data < value) {
        p = p.forwards[i];
      }
    }
​
    if (p.forwards[0] != null && p.forwards[0].data == value) {
      return p.forwards[0];
    } else {
      return null;
    }
  }
​
  public void insert(int value) {
    int level = randomLevel();
    Node newNode = new Node();
    newNode.data = value;
    newNode.maxLevel = level;
    Node update[] = new Node[level];
    for (int i = 0; i < level; ++i) {
      update[i] = head;
    }
​
    // record every level largest value which smaller than insert value in update[]
    Node p = head;
    for (int i = level - 1; i >= 0; --i) {
      while (p.forwards[i] != null && p.forwards[i].data < value) {
        p = p.forwards[i];
      }
      update[i] = p;// use update save node in search path
    }
​
    // in search path node next node become new node forwords(next)
    for (int i = 0; i < level; ++i) {
      newNode.forwards[i] = update[i].forwards[i];
      update[i].forwards[i] = newNode;
    }
​
    // update node hight
    if (levelCount < level) levelCount = level;
  }
​
  public void delete(int value) {
    Node[] update = new Node[levelCount];
    Node p = head;
    for (int i = levelCount - 1; i >= 0; --i) {
      while (p.forwards[i] != null && p.forwards[i].data < value) {
        p = p.forwards[i];
      }
      update[i] = p;
    }
​
    if (p.forwards[0] != null && p.forwards[0].data == value) {
      for (int i = levelCount - 1; i >= 0; --i) {
        if (update[i].forwards[i] != null && update[i].forwards[i].data == value) {
          update[i].forwards[i] = update[i].forwards[i].forwards[i];
        }
      }
    }
      
    while (levelCount>1&&head.forwards[levelCount]==null){
      levelCount--;
    }
  }
​
  // 理论来讲，一级索引中元素个数应该占原始数据的 50%，二级索引中元素个数占 25%，三级索引12.5% ，一直到最顶层。
  // 因为这里每一层的晋升概率是 50%。对于每一个新插入的节点，都需要调用 randomLevel 生成一个合理的层数。
  // 该 randomLevel 方法会随机生成 1~MAX_LEVEL 之间的数，且 ：
  //        50%的概率返回 1
  //        25%的概率返回 2
  //      12.5%的概率返回 3 ...
  private int randomLevel() {
    int level = 1;
​
    while (Math.random() < SKIPLIST_P && level < MAX_LEVEL)
      level += 1;
    return level;
  }
​
  public void printAll() {
    Node p = head;
    while (p.forwards[0] != null) {
      System.out.print(p.forwards[0] + " ");
      p = p.forwards[0];
    }
    System.out.println();
  }
​
  public class Node {
    private int data = -1;
    private Node forwards[] = new Node[MAX_LEVEL];
    private int maxLevel = 0;
​
    @Override
    public String toString() {
      StringBuilder builder = new StringBuilder();
      builder.append("{ data: ");
      builder.append(data);
      builder.append("; levels: ");
      builder.append(maxLevel);
      builder.append(" }");
​
      return builder.toString();
    }
  }
}

总结