poj3565Ants(KM-几何与图论的结合）

链接

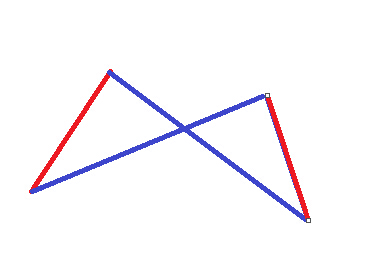
可以看出蓝的之和一定比红的之和要大，也就是说符合条件的匹配一定是权值最小的，所以二分图的最佳完美匹配。。KM

 #include <iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<stdlib.h>
 #include<vector>
 #include<cmath>
 #include<queue>
 #include<set>
 using namespace std;
 #define N 110
 #define LL long long
 #define INF 9999999999.0
 const double eps = 1e-;
 const double pi = acos(-1.0);
 const double inf = ~0u>>;
 struct point
 {
     int x,y;
     //point(int x=0,int y=0):x(x),y(y){}
 }p[N<<];
 double dis(point a,point b)
 {
     return sqrt(1.0*(a.x-b.x)*(a.x-b.x)+1.0*(a.y-b.y)*(a.y-b.y));
 }
 double dcmp(double x)
 {
     if(fabs(x)<eps) return ;
     return x<?-:;
 }
 double w[N][N];
 int n,link[N],x[N],y[N];
 double lx[N],ly[N],slack[N],d;
 bool match(int u)
 {
     x[u] = ;
     for(int i = ; i <= n ; i++)
     {
         if(y[i]) continue;
         double o = lx[u]+ly[i]-w[u][i];
         if(dcmp(o)==)
         {
             y[i] = ;
             if(!link[i]||match(link[i]))
             {
                 link[i] = u;
                 return true;
             }
         }
         else if(slack[i]>o) slack[i] = o;
     }
     return false;
 }
 void km()
 {
     int i,j;
     for(i =  ;i <= n ;i++)
     lx[i] = -INF;
     memset(ly,,sizeof(ly));
     memset(link,,sizeof(link));
     for(i = ; i <= n ;i++)
         for(j = ; j <= n ;j++)
         lx[i] = max(lx[i],w[i][j]);
     for(i = ; i <= n ;i++)
     {
         for(j = ; j <= n;j++)
         slack[j] = INF;
         for(;;)
         {
              d = INF;
             memset(x,,sizeof(x));
             memset(y,,sizeof(y));
             if(match(i)) break;
             for(j = ; j <= n ;j++)
             if(!y[j]&&d>slack[j]) d =min(d,slack[j]);
             for(j = ;j <= n ;j++) if(x[j]){lx[j]-=d;}
             for(j = ;j <= n ;j++) if(y[j]){ly[j]+=d;}
            // else slack[j]-=d;
             //cout<<",";
         }
     }
 }

 int main()
 {
     int i,j;
     while(scanf("%d",&n)!=EOF)
     {
         //init();
         for(i = ; i <=n+n; i++)
         scanf("%d%d",&p[i].x,&p[i].y);
         for(i  =; i <= n ;i++)
             for(j = ; j <= n ; j++)
             {
                 w[i][j] = -dis(p[i+n],p[j]);
             }
         km();
         for(i = ; i <= n ;i++)
         printf("%d\n",link[i]);
     }
     return ;
 }