POJ3321 Apple Tree (树状数组)
| Time Limit: 2000MS | Memory Limit: 65536K | |
| Total Submissions: 16180 | Accepted: 4836 |
Description
There is an apple tree outside of kaka's house. Every autumn, a lot of apples will grow in the tree. Kaka likes apple very much, so he has been carefully nurturing the big apple tree.
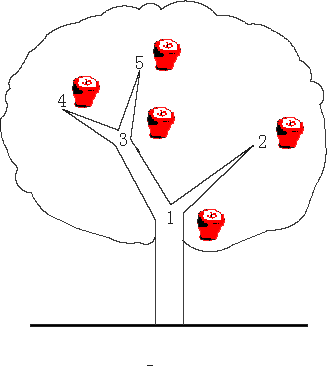
The tree has N forks which are connected by branches. Kaka numbers the forks by 1 to N and the root is always numbered by 1. Apples will grow on the forks and two apple won't grow on the same fork. kaka wants to know how many apples are there in a sub-tree, for his study of the produce ability of the apple tree.
The trouble is that a new apple may grow on an empty fork some time and kaka may pick an apple from the tree for his dessert. Can you help kaka?
Input
The first line contains an integer N (N ≤ 100,000) , which is the number of the forks in the tree.
The following N - 1 lines each contain two integers u and v, which means fork u and fork v are connected by a branch.
The next line contains an integer M (M ≤ 100,000).
The following M lines each contain a message which is either
"C x" which means the existence of the apple on fork x has been changed. i.e. if there is an apple on the fork, then Kaka pick it; otherwise a new apple has grown on the empty fork.
or
"Q x" which means an inquiry for the number of apples in the sub-tree above the fork x, including the apple (if exists) on the fork x
Note the tree is full of apples at the beginning
Output
Sample Input
3
1 2
1 3
3
Q 1
C 2
Q 1
Sample Output
3
2
题目大意级是说,给你一颗树,最初每个节点上都有一个苹果,有两种操作:修改(即修改某一个节点,修改时这一个节点苹果从有到无,或从无到有)和查询(查询某一个节点他的子树上有多少个苹果)。
由于此题数据比较大(N<=10^5),而且不是标准的二叉树,所以这里我们队每一个节点重新编号,另外为每一个节点赋一个左值和一个右值,表示这个节点的管辖范围。
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAv8AAAEBCAIAAABg6V2BAAAAAXNSR0IArs4c6QAAAARnQU1BAACxjwv8YQUAAAAJcEhZcwAADsMAAA7DAcdvqGQAACajSURBVHhe7d0/rutGtsXhHsgL3yicdNoDMRx4Hk5u1GN4gQGnHXgAxgWcdGTAUcOBYcDoxIaDBm7Qgd8+p5YoapGU+KdIVrF+H1bgq10SyWJR2kfSOf7LnwAAAC2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+wEAAG2h+9nV71/97Z9/fc/n33zSbQAA4FR0Pzv45dfPb01PF7ofAAAKQfezA7ofVIw3LAFcH93PDt66nx+//iX+69PXX/JCghrQsgNoCd3Pruh+UAm6H2AHv/3P//ajW1EAup9d0f2gErxhCWRlfU8/GoFT0f3sihcSVIdFC2xl7c4wGofz0P3sihcSVCfbouXpHm2ylT8VjcZJ6H52RfeD6mRYtPYs349GAGfa8RcbbcE/j+6DM9D97IruB9XZumjt+X0YjQMOdshX+221P4/ugzPQ/eyK7gfV2bRo7cl9KhoNHGn/7sfW+ZzonmfoJkH/bgzdz66WvZCUc1WgYeu7H1vAz6P7AIfZ/xcbh4vcbhkm3fF46fC76NaW0P3sau41ZtdDPxoBHITuB5dH90P3Q/ezi/tX6kby5a8/a5jYxTCMxgFHWPnCYIt2TnRP4Gh0P3Q/dD+7WND92JUwFY0Gdpen+xneMky6I3C4g7qfOdE9D5cOv4tubQndzx7mdj92GTyP7gPsYtkblkPD5Wq3DJPuCByu4u7n529+vF+Yb/npoyrLPD7IW1RoBt3PmewyeB7dB9gF3Q/asVf3E2yRP4/uM9foRZq+x73M4EHeoloz6H5OY5fBnOieQH6Zu5850T2Bo9XY/UxdoXQ/K9H9nGZ4Gdgtw6Q7AgWytTonuidwtB27n2Dr/El0hxk+fri3Kf19/viB7mclup/TDC8Du2WYdEegTLZcn0f3AU5Qyns/Ed3tud7facyyw+mhLKo1g+7nNMNrwG4ZJt0RKJMt1+fRfYATVPat5/s3nWd8Bj2HHu0xqjWD7uc0dg3Mie4JlMpW7JPoDsBxtn657Tlb4aMZHZbu/kT3sdd7r9Y/imy/8BVRrRl0P6exC2BOdE+gSLZcX0Z3Aw5ydPejwoANi6gw7v5O1VffDP9XZYu/9/N494doRBvoft7YCkhRbU92ATyP7gMUyZbrnOiewEF27H5sbUdUGGMjIyqMu3c/41m45373XjSiDXQ/Zy4FuwCeR/cBymNrdTSjw9LdgarZqo6oMM3GR1QY0e9+7u/09H4LbNnbP7d7jUQj2kD3c/JSsAvgSXQHoDy2ViMqDNiwiApAnWw9p6j2lN0looKb+o5291YW3c8adD/VvPcT0d2AktgqjagwxkZGVADqZOs5osIrdq+ICgPd73w9dD/3X4On+1mD7ue0pWDrfk50T6AYtkQjKkyz8REVgNrYSo6oMI/dN6KC+f6n26vS6Cdfy37z63avkWhEG+h+zlkKtuJHMzos3R0ogS3OFNWesrtEVADqYWs4osIS9ggRFR48++Lz0j9ZZHe3aFAD6H5K6X5UGLBhERWAs9nKjKjwit0rogJQCVvAKaotYY8QUcFN/MLah99Vn8fuPnpLI+h+Tuh+bK1HVBhjIyMqAKeyZRlRYR67b0QFoAa2eiMqLGePE1FhoP9/+1r6dZ+kd/e3jN7SCLqfo7sfW+URFabZ+IgKwElsQUZUWMIeIaICUDZbtxEV1sr7aE8MX+OGtzSC7ufQ7seWeIpqT9ldIioAh7OlmKLaEvYIERWAgtmijaiwgT1gRIXchq9xw1saQfdzcvejwit2r4gKwOFsKUZUWM4eJ6ICUCRbrimqbWOPGVEhq+Fr3PCWRtD9HNf92MqOqDCP3TeiAnAgW4QRFdbK+2jAfmytpqi2mT1sRIWshq9xw1saQfdzUPdjyzqiwhL2CBEVgEPY8ouosIE9YEQFoDC2UCMqZGIPHlEhE3uBi4zenm68PLqfI7ofW9Apqi1hjxBRAdifrb0U1baxx4yoABTDlmhEhaxsExEVcrAXuMjUjS2g+zmn+1FhOXuciArAnmzVpai2mT1sRAWgDLY+IyrkZluJqJCDvcBNRaOvju5n9+7HlnJEhbXyPhowh626iAqZ2INHVADOZiszRbUd2IYiKmxmL3BT0eiro/vZt/uxRRxRYQN7wIgKwD5svUVUyMo2EVEBOJUty4gKu7HNRVTYxl7gpqLRV0f3s2P3Y8s3RbVt7DEjKgC52UqLqJCbbSWiAnAeW5MRFfZkW4yosJm9xg2jcQ2g+9mr+7G1m6LaZvawERWArGyZpai2A9tQRAXgDLYaIyrsz7YbUWEze5nrRyPaQPdzXPejQib24BEVgHxsjUVU2I1tLqICcCxbhymqHcI2HVFhG3uZ60cj2kD3s8tSsCUbUSEr20REBSAHW10RFfZkW4yoABzL1mFEhaPY1iMqbGMvc/1oRBvofvIvBVuvERVys61EVAA2s6UVUWF/tt2ICsBRbAVGVDiW7UNEhQ3sZa4fjWgD3U/mpWArNUW1HdiGIioAG9iiSlHtELbpiArA/mztRVQ4g+1JRIW17GWuH41oA93P7t2PCruxzUVUANayFRVR4Si29YgKwM5s4aWodgbbk4gKa9nLXD8a0Qa6n5xLwdZoRIU92RYjKgCr2HKKqHAs24eICsBubMmlqHYe25+ICqvYy1w/GtEGup9sS8FWZ0SF/dl2IyoAC9lCiqhwBtuTiArAPmy9RVQ4W8a9spe5fjSiDXQ/eZaCLc0U1Q5hm46oAMxmSyhFtTPYnkRUAHZgiy2iQgFsxyIqLGcvc/1oRBta737s3I9GQ5+ydRlR4Si29YgKwDy2flJUO4/tT0QFICtbZhEVimG7F1FhIXuB60cj2tB092MnfioaPc1WZESFY9k+RFQAZrDFE1HhbGXuFa7E1liKasWw3YuosJC9wPWjEW2g+3kdjZ5gyzGiwhlsTyIqAE/ZsomoUADbsYgKQCa2wCIqFMZ2MqLCEvYC149GtIHu53U0eowtxBTVzmB7ElEBmGZrJqJCMWz3IioAm9nSiqhQJNvViAqz2QtcPxrRBrqfkRM/dbuxJZii2nlsfyIqAGNstaSoVgzbvYgKwDa2riIqlMr2NqLCbPYC149GtIFvPfu5t1siaeSQLcGICmcrc69QJlstERUKYzsZUQFYy1ZUimoFsx2OqDCPvcD1oxFtoPvxcz+8ZZQtvogKBbAdi6gAPLJ1ElGhSLarERWAVWw5RVQonu12RIUZ7DWuH41oA92Pn/vhLUO27CIqFMN2L6ICcGMrJKJCqWxvIyoAy9laiqhQA9vziAoz2GtcPxrRBrofP/fDW4ytuRTVimG7F1EBeGfLI0W1gtkOR1QAlrBVFFGhHrb/ERVesde4fjSiDXQ/fu6HtxhbcBEVCmM7GVEBqHl52G5HVADmsfWTolpV7BAiKjxlr3H9aEQb6H783A9v6bOlFlGhSLarERXQNlsVERVqYHseUQGYwRZPimq1saOIqPCUvcb1oxFtoPvxcz+8pWPrLKJCqWxvIyqgYbYkIirUw/Y/ogLwiq2ciAp1smOJqDDNXuP60Yg2tN79BDv9/WjEO1thKaoVzHY4ogKaZIshRbWq2CFEVACm2ZqJqFAzO6KIChPsZa4fjWgD3c/67keF4tluR1RAY2wZpKhWGzuKiArABFswERUqZwcVUWGCvcz1oxFtoPuZtRRsbUVUqIHteUQFNMaWQUSFOtmxRFQABmyppKhWPzuuiApj7GWuH41oA93P66VgqyqSbq+I7X9EBTTDFkBEhZrZEUVUAB7ZOomocBV2dBEVBuxlrh+NaAPdz4ulYOspJd2xLnYIERXQADv1ERUqZwcVUQHosUUSUeFC7AAjKoyxV7oU1ZpB9/Os+7HFlKK71caOIqICrs7Oe4pq9bPjiqgAvLPlEVHhcuwwIypgDN3Psu5H96mTHUtEBVyanfSICldhRxdRAc2zhZGi2hW1c6Tb0f28saYnxZZRRKNrZkcUUQEXZac7osKF2AFGVEDzbGFEVLgoO9iIChig+3ljfU/KJdeQHVREBVyRneuICpdjhxlRAQ2zJRFR4dLskCMq4BHdzxvre1KuuoDsuCIq4FrsLKeodkXtHCnmsPUQUeHq7KgjKuAR3c8b63tSLrx6+oeWogIuxE5xRIWLsoONqID22EqIqNAGO/aICuih+3ljfU/KhddNd2hdVMBV2PmNqHBpdsgRFdASWwMpqjXDDj+iAm7oft5Y35Ny7RXTXRJdVED97MxGVLg6O+qICmiJrYGICi2xGYiogBu6H7HWJ3L5FdNdFZc/0qbYaY2o0AY79ogKaIOd/YgK7bF5iKiAd3Q/0lrrE7pLoosKqJad0BTVmmGHH1EBV2fnPaJCq2w2IiqA7qcz7H5UuLT+VZGiAupkZzOiQktsBiIq4NLspKeo1iqbjYgKoPtJYk1Y96PC1fWvihQVUCE7lREV2mPzEFEB12VnPKJC22xOIio0j+5Hi6PN7id0l0QXFVAVO4kRFVplsxFRAVdk5zqiAsYmJ0XlVrXe/fSXQoOtT9KfhBQVUAk7fSmqtcpmI6ICLsdOdEQFvLPJsWhQe+h+WApMQvXs9EVUaJvNSUQF1MzOZvfPflIJHZsfiwY1punux1ZARIX22DxEVMBGv/z6ee8T1b/+7cevf1ElFztxERUw/aSvMqpiJ3EqGo0em6JhNK4l7XY/du4jKrTKZiOiAlb6/auHvueez7/5pCGb2SmLqIB3NjkWDUIN7NxNRaPxyGZpGI1rSaPdj534FNVaZbMRUQErTXY/q98BslPT/bOfVELH5seiQSibnbWpaDQe2SxNRaObQffT6IkfZXMSUQFrvHc/X/76s/7555/f/9Q1QEvf/rHzMhWNRo9N0TAah4LZKRuNhmLAJmoqGt2Mkrqf/b8hkdgpj6iA6etEZSzw+9eDFufjh9vy/vC7bprBzsVUNBqPbJaG0TiUys7XVDQaAzZRU9HoZhTS/RzxDYnEzndEBbyzybFoENbqup/5C9tOwVQ0Go9slqai0djV2p9v7WRNRaMxYBM1FY3O7edvfuyd9MhPH1U5Wendz8Z3gOy8dv/sJ5XQsfmxaBDWuK/zr77XTS/Z/I9GQzFgEzUVjcZeNv18aydrKhqNgeFE2S0paXBWo+d9r091liqp+8n0DYnEzutUNBo9NkXDaBwWuv8M1F/qT9nMT0WjMWATNRWNxl42/XxrJ2sqGo2B4UTZLSlpcD5TJ53u50G2b0gkdlKnotF4ZLM0jMZhid7bvwsufpv5qWg0BmyipqLR2Mv6n2/tTEVGb4yk8RiyiZqKRi/RnUT9u+f+Cv54ij9+oPt5ZcU3JBI7o1PRaDyyWZqKRmOe/iff8z/zCjbtU9FoDAwnym5JSYOxm/U/39qZijy/vSjdVT+MRhzF5moYjVvi2RH1vuO17tObAxTb/dzfNFv0ahHspI5GQzFgEzUVjcYMvZ+BFv/QY9M+FY0e+uM/n/3fv//yns9++K9ubMlwouyWlDQYR5rz862dpi6jpXSXWfz71xVEe76WzdUwGrfEkz1c8Sn/8QrtflbPnZ3RqWg0BmyipqLReOHT1192zw6Lf9PB5jwyemMkjR/479//odaH7ud5NBrHef3zrZ2j59F9ZulfldeJDm6azVg/GrHQkx14bG37XwAq5Re+Qondz7pvSCR2Uqei0RiwiZqKRuOZ3jW//LtrweY88vx2868ffutan2a7n2BzNYzG4UBzfr610/Qyutsr/Y+hLxYd4TSbsS4qLzS99Xt/+dU3w7fZ+N7PhP7SXPqZV7CTOhWNxsBwouyWlDQY0178fPnys3Cb8C6jpXSXBz//8d70/PbZ7e2fRd1P2kn9o3I2V8NoHI4y5+dbO0dzons+p29bX7MB0jE+ZZOWotpC01t/9e5aGR+HldX9bPmGRGIndSoajYHhRNktKWkwpm3qfmy2n0f3efDpi/SWz3efvv1ucffT30/dVDmbsX40AkeZ8/OtnaPI1O39pDFP3d6O/fB7tw9XyvsxTj/z9HqO5VM3wh5ft77p78P9pXz763te5XQ//fla+dGgndHI6I2RNB5DNlFT0WhMOq77iehuN7eO549v7/+9svuJ6NbK2Yx1URmHmPP6ZycoRbVXl4YGTbht/e315bYb14kO8qjuxx/8Par19uHxia77MgDdz93Wb0gkdkYjz2/HKJurYTQO+7DZnhPdM9FnXv/+4v2pbmn3o8uwFxXqZ5OWohp2N/fnWztBERXGzB/Z/YWh9IZTrw+rJu+H8VIJ3c/9Hb6H7uf+q3Z0P7Lpp+SOnc4uo6V0F4yyuRpG47ADm+rI1O39pDHvbp95/eM//3r/N92PmZ467Gfuz7d2diIqTJg9+LYDtw6g635mvr6so0OeiAZl1r2ePuswZs/bpP6BdFEt3P+a5X03eh1nEb/5lbn7uR3bPSo8k6H7sXP5PLoPptmM9aMR2IFNdYpqrxZ5GnPrdX77+x/pBrofNzpv2NPcZ3g7NZF0+xM2PqLCo9vr7sgr8a7dzxnK6H6envRC5jxn92NH2EXlSUd3PxHdDdNsxrqojB3YVEdUGDMy8vaZV7/RofsxI/OGfe3Y/YTXd7m9D9F/KaH7eTFpr6TZs6gmvTf8+tnw5Za8Suh+trITOSe6J56ySUtRDbnZPEdUmDAcbH/gZzQveyC7eCMqXMVw3rCzWd2PnZdIuvNLL+815w/8XKgHGp1t/6Tp5aS9NNjEW1Tr6X3aFXnWkB2v+u7HzmJk6vZ+0hjMwdQdwCY5osI0Gx+h+5nDJk234lR2UiIqzGB3jKhwQ/eT0j/G5zM2hz14imqVqLv7sVOYotpEtYsG4RXm7QA2yREVnppzFz75MnMmDUeyM5Ki2jwr7lv7J1/d5RnRTfLknTa99bJiuoYGD/4W1Spxte5HhTHzR6KPedubzXBEhVfm3Ivux8yZNBzJzkhEhdlW3L3q7qe7NruoMKb/1lc62BXTNdQ9pkXlGlTc/dgpjKgwYdFgdJi3Xdn0RlSYwe4YUaFne/cTUe0SXs4YjmSnI6LCEiseoZ3up/9uUK7up9vuMBpRg1q7Hzt/ERWm2fiICniKSduPzW2KavO8vO+i7seu3C4q1+/ldOFIdjoiKiy39HHofubP1VC33WE0ogYNdT9hxV3ApO3H5jaiwmwb727syu2icv3yThc2stMRUWG5XI9TBbs8IyqEX379/PH/Idr/rav0d663z1X3gMNoRA2q7H7s5EVUeGXdvRrHpO3EJjaiwhLbH6HPrtwuKtcv73RhCzsXERVWyfhQ5bPLM6JCuP/fJAa5dUXb58ofuReNqEF93Y+duYgKM9gdIypgGjO2B5vViArL5XqcYFduF5Xrl3GusIWdiIgKa9mjRVS4Irs8IyqEye7n/id/tk/U4MHv0YgaVNb92GlLUW2eLfdtENO1E5vYiArL5XqcYFduF5Xrl3GusJqdhRTVNsj+gMWyyzOiwrv+R10p6QOvzvaJssfvRyNqUH33o8JsG+/eGqZrDzarERVWyfhQduV2Ubl+GecKq9lZiKiwzR6PWSa7PCMqzLN9omzr/WhEDWrqfuycRVRYYvsjNIXpys6mNKLCWvZoERWWsyu3i8r1yzVRWM1OQUSFzexhIypcjl2eERXm2T5LtvV+NKIG1XQ/dsIiKiyX63FawFzlZfOZotoGuR7QrtwuKtcv10RhHZv/iAqZ7Prg5bDLM6LCPBtnabjp4S1VoPvhGfAZ5iovm8+ICtvkeky7cvvRiMrlmiisY/MfUSGTXR+8HHZtRlSYZ+MsDTc9vKUKdXQ/drYiKqyS8aEuj7nKyCYzosJm9rARFZawy9aiQZXbPktYzSY/okI+9vgRFa7Frs2ICvNsnKLhpoe3VKGC7sdOVUSFtezRIipggInKxWYyokIm2x/cLluLBlVu+yxhHZv5iAq5HbOVc9m1GVFhno1TZJseRuOKV3r3Y+cpRbUNsj/gVTFRudhMRlTIZPuD22Vr0aDKbZ8lrGDTnqJabsds5Vx2bUZUmGfjFNmmh9G44tXX/aiwzR6PeUlMVBY2jREV8rHHj6gwm122Fg2q3MYpwjo27REVdmAbiqhwIXZtRlSYZ+P82KaH0bjiFd392EmKqLCZPWxEBTxilrazOYyokNvGrdhla9Ggym2cIqxgcx5RYTcHb+54dm1GVJhn+/zY1vvRiBqU2/3YGYqokMmuD34ZzNJGNoEpquW2fSt25XZRuX7bpwiL2IRHVNjT8Vs8mF2eERXm2T4/tvUuKleC7meXB78MZmkjm8CICjuwDUVUmM2u3C4q12/j/GApm/CICns6fosHs8szosI82+fHtt5F5UoU2v3Y6YmokI89fkQF9DBFW9jsRVTYzcbN2ZXbReX6bZwfLGKzHVFhf2dt9xh2eUZUmGf75NjWu6hciWzdj82CRYPmsXMTUSG3Y7ZSNaZoNZu6iAp72rhFu2y7qFy/jfOD+WyqIyoc4sRNH8Auz4gK82yfHNt6F5UrUVz3YycmRbXcjtlK1Zii1WzqIirsaeMW7bLtonL9Ns4P5rOpjqhwiBM3fQC7PCMqzLN9cmzrXVSuRAXdjwo7sA1FVMAN87OOzVtEhf1t2a5dtl1Urt+WycF8Ns8RFY5iW4+ocAl2eUZUmGf7zNjWu6hcibK6HzsrERV2c/DmqsP8rGCTFlHhEFs2bZdtF5Xrt2VyMJNNckSFY5WwDzuxyzOiwjzbZ8a23kXlShTU/dgpiaiwp+O3WBfmZwWbtIgKh9iyabtsu6hcvy2TgzlshlNUO1YJ+7AHuza7qDzD9pmxTXdRuRJ0P0dvsS7Mz1I2YxEVjmJbj6gwg122XVSu3+qZwUw2wxEVDme7EVGhcnZtdlF5hu3TYpvuonIlsnU/wSaii8pP2fmIqLC/s7ZbBSZnEZuuiArHWr0PduV2Ubl+q2cGc9j0RlQ4SVE7k4tdm11UnmH7tNimu6hciSK6HzsZERUOceKmy8fkzGdzlaLasVbvg125XVSu3+qZwUs2txEVzlPa/mRh12YXlWfYPi226S4qV4LuhyfEZ5ic+WyuIiocznYjosIrduV2Ubl+66YFc9jcRlQ4j+1PRIWa2bXZReUZts+JbbqLypU4v/uxMxFR4Si29YgKyHGdNMImKqLCSdbtjF25XVSu37ppwUs2sREVzlbmXm1h12YXlWfYPie26S4qV+Lk7sdOQ0SFY5WwD2ViZuawWYqocJ51+2NXbheV67duWvCczWpEhQIUu2Or2bXZReUZts+JbbqLypU4s/uxc5Ci2rFK2IcyMTNz2CxFVDiP7U9Ehafsyu2icv1WzAmesylNUa0AtmMRFapl12YXlWfYPiG26S4qV6Ks7keFw9luRFRoHtPykk1RRIWzrdgru3K7qFy/FXOC52xKIyoUo/DdW8EuzxTVZtg+IbbpLipX4rTux05ARIWTFLUz5WBanrP5iahQgBU7ZlduF5Xrt2JO8ITNZ0SFkpS/h0vZ5RlRYZ7tE2Jb76JyJc7pfmz2Iyqcp7T9KQTT8oRNTopqBbAdi6gwza7cLirXb+mE4AmbzIgKhbGdjKhQLbs8IyrMkGUqbOtdVK5Ezu4n2FykqNZjJyCiwnlsfyIqtI05ecImJ6JCMZbunl25XVSu39IJwRM2mREVylPLfs5kl2dEhRmyTIVtvYvKldi9+1Ghx2Y/osLZytyrczEnU2xmIiqUZOke2sXbReX6LZ0QTLGZjKhQpIp2dQ67PCMqzJBlKmzrXVSuxNHdj019RIUCFLtjJ2JORtm0RFQojO1kRIUJdvF2Ublyi6YCT9hMRlQoVV17+5JdnhEVZsgyFbb1LipX4tDux+Y9RbUC2I5FVGgYEzLKpiWiQnkW7addvF1UrtyiqcAUm8YU1QpW3Q4/YZdnRIUZssyDbb2LypU4uftRoRiF797xmJAhm5OICkVatKt28XZRuXKLpgJTbBojKpStxn2eYpdnRIUZssyDbb2LypU4rvuxSY+oUJLy9/BgTIixCYmoUKqle2vXb0SF+i2dCgzZHEZUKF6luz3KrtCICjNkmQfbeheVK3FQ92MzHkm3l8Z2MqJCk5gKYxOSolrBqtvhnTAPG9kERlSoge15RIUK2YtsRIUZck2C7UCKapWg+3G17OcBLjoVn77+8nGVfvnrzyq9YBMSUaFsNe7zHpiHjWwCIypUouqd73t4+nqPCjNknATbh4gKlTii+7HpjqTBZapoV/d2xakYtD63fPW9Rkyx2YioULxKdzs75mELm72ICvWoff879twVUWGGy0zCdpm7n2BnxeY6onGlqmtvd3XFqZjsfp6/A2RTEVFhmf/+/R///sv/9fKP//xLpR3ZnkdUaAyTsJpNXUSFqtghRFSojT930f2ssq77efbZQf92m+gUjStYdTu8kyvOQyzdnz7qv998/NAt14fbjU1FRIUFBq3PLV/M/OBtg807fwVMwmo2dREVanONo+heYbuoMMM1ZiCLFd3P688O0j/jP2yiI2lA4Wrc5z00MQ/f/3RbwJPdj81DRIVlJrufA94ByrH/1WMSVrvM1F3jQG5PWfeoMMM1ZiCLnN2PfXZgsxxRoXiV7nZ2DcxDbzF/+F23PbJJiKiwWHQ/f3yr/37z7XddA/Rw+x7sECIqtIQZ2OIa89YdRRcVanN/2X2Pbp3hGoefxbru5/VnBzbFERVqYHseUaExF52EsfZ9+ks/NgkRFbb7+Y/Dup+w11HUgxlAuMYy6D996aZ5rnH4WeT41vPYZwc2xREVKlH1zudy0UkYdD8T7/oku01C74Ow7z7ptj3lOZA//vOZOrZ/f/bDf3VjJfLMACp3mWWQnr70j9kuc/jbbe9+Rj47sPmNpNsrUvv+Z3HRSRh77+dv//z8m8kWJN8MjH3155Bf+wrdUXRRYYGH/af7QY1sGURUaEPLx27WdT/PPjuwyY2831wZO4SICi1pYQZ6n9v++PUvunE3g+4n47s+v/z6+e1inOrkNp7Qf/3wW3/n6X5QqZZXQsvHbjJ1P73PDmxyIyrU5hpHsUUbM3BfzE/e/slk7L2fPG3EwyW5S/ejbyn99tntEOh+6jd4Jn/6V69qNfjBoPGV0OyBm3zv/VxuYV3mQFZrYwaO7H4e9H7n67e//6Eb1/n5mx+7y/DJgdgJjajw2qcv0q5+96nbbbqfyo0/jUde/t3zqoz8YMBKQMjwrefhZwfXWFXdUXRRoRkXPPzvf7LvOPf7hsOf9O9vBW3qJPRrBz9+PqONW3dObx3P2++m0f1cxWT3k+8doMGbnUd9y60z9YPBvsvg1F8OsEN+/ndcN7JPw4/59dVcMnQ/J/70vLfuCtnxOinYBQ///vuJw+z4HDEhS/fz+1dp/z/83v0ckrn7uf1mfvqb1PV2P2HZgV9cPG+//tslG4x/zhs54I+by5IfDPJ5OPBjL5Pbs8FDdvpG4+394IdsfRv7SHQ/z3TPlW0+Y17w8Ce7n/2/8hw9xON3nPs/Nq1+Pbi9Yr29XO3T/dye424/tVfd/eCZ+9Wxb/dz1DtAy34wyOW8Xw4YbX0iezy5jbY+kWt3P3GFFPTZwb7spSKiQhsueey9H3CVg1r2+982HGbt28W3l6t03c18il90Qm+9zv1Jje7nonofhD39C1izRffzsLC7lXPM5yNLfzDI47xfDug/s/UP8+OH/N1P71Q+HOC3312++7lN8SBZfmIoS/dSMf8F4zJaPvb8Jruf1c8Xtx/1bt/SyP8Uf9vnxyc47TndT/3Gvvqz36993S+B/bufVT8YbHbeLwfM+IMX2dT8J0/7MnY/+392cIbGO4BmD3wP/R+Ytj933J7Q79dd9qf4wVcaR0IPVLNB95PnXZ9RvQ/Cdv/j5vv/YDDmdoG/9XYHdz/3T2D2/5sF96eFw7/Dntea7/10K6nL7s3mebqXf5oAFOT2Q0j/0qP7wUJj7/3kfD4f++rP/i+ZB/xgMOL2ztYpvxzweID9LwDl/0Dm8dD6XwA64gPNjLJ86/niaH1QmsEvtY5kpyf6g5/WcZjej7W53sgfdD8H/C/tDvnBYODcXw64d7FffXP/COyWvB/L3M/pFz/cPwK7pbnf+QJwKLof7OD+Ippp8Yy997Pzyjnl0rhdFGf9csD4e3j35Pw4bPyc3lPPx2F0P8BFHPH2Pt3PlWXvfh50K2fXdwhO6H7O/+WAfvcz8nlf1rd/+t3PSLdX0ds/dD/ARdD9YIHvj//bJfcXzoMXz66XRgFfj5tqW7svAO3S/TweVPcFILofAMc6pvvBRUz+9m5kp79dQvezl65zfTjA+6/B5/zqT3e8Dwd1/zV4uh8Ax6L7wQJ7/+2Sn3f54+brHH9pHP0W6f1sjn7ylbWdvf/dptFPvqr5zS+6HwBoUe/VUcnZHNxfI4c5+gXy+t3P0y8+5z7qZ198PvhdvS3ofgAAuU12P9V8MrLFGV+Pm/j/fO3yFywn/j9fB/xFg3zofgAA+fU+DVEqemNgozO6nzeP7+fl/LrP0OP5ra+ppfsBjtN7YsoWPTQAYDa6HyAb60tKiPYMANBD9wPkYW1HUdEuAgDe0f0AGVi3UWC0owAAuh8gC2s1Cox2FABA9wPkYt1GUdEuAgDe0f0A2VjPUUi0cwCAG7of4EzWqbyM7gYA2IDuBwAAtIXuBwAAtIXuBwAAtIXuBwAAtIXuBwAAtIXuBwAAtIXuBwAAtIXuBwAAtIXuBwAAtIXuBwAAtIXuBwAAtIXuBwAAtIXuBwAAtIXuBwAAtIXuBwAAtIXuBwAAtIXuBwAAtIXuBwAAtIXuBwAAtIXuBwAAtOTPP/8fOk+J1EA1U1gAAAAASUVORK5CYII=" alt="" width="728" height="244" />
上图也就是DFS搜索的时候做标记的过程,这样新的编号为1~6的节点所管辖的范围分别就是[1,6] [2,4] [3,3] [4,4] [5,6] [6,6],其中左边的是左值,右边的是右值,节点1的区间是[1,6],正好这棵子树有6个节点,其他也一样
那我们吧新的节点放进树状数组时
aaarticlea/jpeg;base64,/9j/4AAQSkZJRgABAQEAYABgAAD/2wBDAAMCAgMCAgMDAwMEAwMEBQgFBQQEBQoHBwYIDAoMDAsKCwsNDhIQDQ4RDgsLEBYQERMUFRUVDA8XGBYUGBIUFRT/2wBDAQMEBAUEBQkFBQkUDQsNFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBQUFBT/wAARCADHAagDASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBAAIRAxEAPwD9U6KKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACkzzS01qAPN/EHxJ1yfxvceHfCOh2utyaO0D6413eG2aGOVdyLCNpEjlfmwSq4BGckCusHjbQ08UR+Gn1KBdfe3+1Lp5fMpj/vY/CuW8beDPCniDxHbX97rsujX9uV+0x2OpfZTdoPmRJwCCwBwR0PbOOK4u48MB/2gl8WJrWinQWtYiSbxAyyIpTb5X8T9CJdw2g7dp60x2Pegc0tYy+LtCUEf2zYD63KD+tKPGGhEZ/tiw/8CU/xpBY2KKy4fFOjXMyRQ6rZSyuQqolwhZiegAzzWmDmgQtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFITigBaQnFJvGcZ5+tYfiTxxofhNFOq6nBZswJWJ3+dsdcKOT1oA3C4H86aWBIHfHFeeS/EXX/EgEfg/wvNc5POoa4zWNoq4yCDtZ3z22IRnqV60r/DfWfEgYeLPFVzeWz/f0/RlbT4MY6FlYynBPUOOmcDpQM474ReCdA8UXnxHutX0ax1S4TxjfxpNdQK7BAkW1QSOg9K9A/4VN4K/6FXSf/ANOf0ry74TeNvCfwlsPiFp+talaeH7a18VahNDDOduICIiHH97JJOeSSTnJzXo8Xxp8DTRo6+JrLbIAwy5Bxj6VaLWx454w+KHwy8Bpq6a14A0zTruwmMUMdw9lGjnBKCSQuEgZ8fKrkEj8cex6T8NfBGr6VZ3y+E9HRbmFJgogikC7gDjcuVP1BIrza4/4V9q+qQa5L8TXu9WtizaZf8AmRN9liJyUA2bZBnuwPQeldl4P+IHw38EeHLHw7pvieyFrp8IRUaXLgEk7mGO5JPTHNNXuBi/HH4feGPD/wAMtQv9N8P6bY3sN3YmOeC3VHQm7hGQRz0J/OvcEGBXhXxq+JXhbxP8Ob7S9K1u11DUbi7sVitoSWdyLuFsAAein8q91U5FQyWOooopEhRRRQAUUUUAFFFFABRRRQAUUUlAC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUhOKAFopu8ZxTJrqK3heWWRYo0G5nchQo9ST0oAkzQWrz69+NGkz39zYeHrDUfFt5bSGKY6Rbl4InBwyNOcRhhxld2eQcYqFtI+Ivi0gX2r2HgzTmBDQ6Qn2u+IOCD50o8uJhjBAjlBBOGHFMZ2+r+ItM0C2a41K/t7CBQSXuJAg9e9cVcfFe41uRo/CHh+88QIAduov/AKPZZBwcSNy/1UEe/WtHRvhD4a0mYXM1iNX1E4L32qMbmZ3zndlshTn+6B6dK7FIhEgVAEUdFAwBSA8/m8HeMPFK41vxL/YsHRrTw+pUkcHPnOMg544GK3PDfw28P+FJJJtP09PtchzJd3LtPMx7ne5JGTzgYGSeK6cDFLQIYEx0NH3fenE4rjviBr1zEttoWkMDrmq5jiOM/Z4uBJM2DnAyB9SKAMG7srT4o+M5oPsdvP4e0S4Md7JLGpa7vUClYypH3EDA7u5wOnNbXxKv7HwX4D1rVo7S0imt7crAzQKVErkJFkY6b2XPtmuj8P6FbeG9HtNNsgVtraNY1Lcs2B95jjlj1J7k1xnxkjbVLXw7oWBImp6rCs8JHyvAp3Pn2DbD68Uxmr8O/A1n4T8C6Ho8un2kc1raqJ0ijBQTH5pNvHQuzEDtmsDw1ounr8YfF5FhbD/RrYZ8legReOnvXpoNcB4dO74yeLCM4FlaqfrtyT+RH5UAdsmlWcbK0drAjKcqwjGVPt6VbAIHNApaQgooooAKKKKACiiigAooooAKKKKAEJwcVDPfQWphEs0cZmbZHvYDe2C2BnqcAnHoD6Vw/jzxdrcfiSx8K+F1sU126tHvjcaoH+zpCrBCMLyzEnoOw561w/7SWvXFp8EbHVb++sfDepieC4+2TBbm3s51Rn3g5DOFIJATLPgIAQxoA9qttZsL2RI7e8t55HTeqxSqxK4U5AB5GHU/8CHqKnW7ha5e3EqGdFDvGGG5VJIBI64ODg+xr88Pg9Z+MdKHg2PS/GFv/wAJUdM0nSLOG10+2uYI0klCX6rMr/O6W9i8megEKLgHr2PxN8Yarbn432cfiOyvoksJzNdWdrcLeGWK22CCUqf3MSD5wUILybwozk0AfcCTpIMowceqnIp4Oa+WP2TJTH8V/iHaxMUtE0XRJEgU3YjDtLqIdgtySwJ2rkjg7R36/Uy9KAHUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUhOKWmnrQAhlVWAJAJ6DPWl3A9Oa8J8b2sTfFbd4ltdeup2vbVvC0mitKscKBY/P8zaQmd4lLeZnKHAwerPCXxpu/E/7Uet+EpBe2OmWejuILK4tJEEssN00clx5hXaVYMm3BJIHTg0Ae9daWm7setBcD6etAC0FgK5vxH8RPD/hZCb7UEMudotrcGWZjxkBFyT1B6dK59PF/i/xTvXQ/Dn9k2rAKL7XHMZBPUrEuSeCMZI5yO1AHoTSKgJPQDNcbq/xf8L6XOLePURqV42AtrpqG4kYnoAEyOeg+orPb4V33iFg3ivxNfatCcFrCzP2S2PfB2fORkKeGHSuy0jw7pugQeTpmnWmnQ8/u7SFY19+FA60xnEDWfiF4vYDTNIs/B2nt/wAvmtt9quz3UrbRnaAw4O+RWXnKnpUknwR0fXSZPFd5f+L2Yktb6nORZnP3lNsmI3Q8ZWQOOB759EC0opCuVdO0y20iygs7G2hs7OBBHDb26BI40HRVUAAAeg4FWlGBilooAKKKKACkJwaWmOcflmgDO8R6/a+GtHutSvGZYLdNxC/eY9Aq+5JAHuawPAfh263y+JNajC6/qCYaPBH2WDOUgA7YGN3qRVC3RPiT4pNzKTL4c0adTbIBmO7u1Y/vN2eVjI4HTdznjn0BelAwyF6157q841X43aJp4Vj/AGdpMuoOJB8h3yeUhX/aBDdex9q9Bc//AK689+HO7WfGvjrXZGYk3qaVDG3Kxpbg52n/AG2kLEdKBHoQBA/wrgPDv/JY/FgPBNnasOf4duB+oNegdPrXn/h7j4x+LMjk2Vrg/wCzt4/XdQB6CKWkFLQAUUUUAFFFFABRRRQAUUUUAFFFFAHN+N/h9o/xAsYrbVop/wB0xaKe0uZLeaPI5CyRkMAeMjODgZ6Csb4gfCyPxZ8P4PCGlT2ug6YpiiJS0ErQQJ0+z8gRTKQrJLhtjKDtNd7RQB4ro/7OLaJYS3MHiWUeKYLl7rTdZS1EYhYlt3mxKwExkDESkkbhjaE2ptd42/ZotviDFdS6r4y8R2uo3nyXM+l3KQRtCY2R4BCVZChLlwXDODjDcV7RRQB5v4C+DTeCPGep+J5/F2veItR1Gwh06ddUkiMZjikkeIgJGpBUzTYOf+Wh9sejgYpaKACiiigAooooAKKKKACiiigAooooAKKKKACmsM0pOKZJOkUbO7BEUZLMcAD3oA8rvb/xx4l+IXiXS9C8Q6XomnaULZUS50prqSRpIg7MW81ABzgDFKPBnxGW9N2PGnh77YYxEbj/AIRk+YUByE3faM4yx49z6074aa/p3iH4l/EW50y9hv7ZJrOJpbdtyh1tlyM9/wAK9KyO/HTvVpFpHm8/hr4rCCTyfHmhNNtPliTw44UtjjJFx06dB61y+q/Cn4t+LLbT/wC2/ifpVqY4iLmw0zQnWCSQ/wAXmfaFcgDIA4HPIrP8ZQapd698VLS3k1h7eW80aSRUkkWMWmIluBAykFRtWTcEIPPWvSPg3bXFp4ISOZbpLUXU32FLyR3kW13nyQS5LH5cY3EmhIehzmhfCrxn4dbdp/inw3av/FNH4aYysPQu1yWP4muz+DnibUfGfww8Oa1qxgbU720SW4a2QpGX7lVJJAPXGTiupGOfcVwX7On/ACRLwh/14pSZLPRgMUtFFSSFFFFABRRRQAUUUhbFAATiuJ8e67d3d7b+FNEcLrN+okmm3FfsdnvCyzDjl+cKOMnntW/4p8R23hbRLnUrpZHihAxFCu6SRiQAir3JOBj3rH+H3hi60y2vNW1dYv8AhIdWk868aIkiNRny4VJycIp/76Lc9KAOg0TRrfQNHtNNs12W1rGIkB6kDufUnqT3JzV9cgc0AYFBOKAKesXw0zSry8Yqq28DykucL8qk8+3Fcp8GLFrP4d6ZIyusl1vum3997Egj2IwR9ab8adSksvh1qkNvse8vtllbxSdHeRwpA99pY57YrrtH06LR9Js7CAsYLWFIIy5y21QFGffAoAtY7V5/4dI/4XD4tC8/6Lakk9m2jj8sc+9egnrXn3hw/wDF4/F2Dx9ltRj32CgD0EUtIKWgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKazhepxXHWHxl8EanDrs1r4m0+aHQ8/2jIJcLb4zkknqODyMjigDs6KqaTq1nrumW2oafcx3dlcxiWGeI5V1IyCDVugAopCQOtIXA7GgBc0yWZIVLOQqgElicAD3NcXqXxTsJNTk0rw/azeJ9UjwJU08jyYM5x5kx+Reh4yTx0qCL4fal4mmF14v1U3iZJXSNOkeG0QZ4DMMNLjHVsDkggigCzqHxHhvr6bS/DEC6/q0XEm19ttB82CJZcEKeDwASaqj4b3nihhL4x1ZtViHTS7QGGz7csB8znjuQMEggiu007S7bSLSO1sbeGzto12pFAgRVA6YA4q0oIHNAHmknw117QvFGr6l4W1aw0uy1JIA1lJZjbCY02ApjsQBxVn+wPiKMD/hJdL/8AzXolc38QfEzeE/C15e26rJqDL5NjC+SJbl+IlI9N3J9ACe1O402ed+H7v4k+IfEuuWtv4g0f+zNNZLb7QLM7pLjG6Qem1dwH1z1GKb4vvPiV4a1PwnbR67pNwNa1ddOkZrQjyl+zTzF19/3IGP9o16V4E8Np4U8K6fpylnmRN9xNJgvLM3zSOxHcsSfT04xXM/FnA8Q/DAEA/8AFUrwTj/lwvaLhckTQfiIGyfEelMM9DZnkelbnw18Ht4A8CaL4ee6+3Pp9uIWuNu3zCO+O1dKvelouFwooopCCiikJxQAtFN3jHHP0pQd2fyoAWo5XWMFmYKAMkk8D608sB14rhvHN5P4i1W28JafM0X2hfN1S5iwxt7bnCkZ4MhBUegyfqAVrCP/AIWJ4v8A7SlzJ4d0d1NgCo8u6uupnVupCY2gdCSx7CvQVJI5qrpWl22i6ba6fYwpbWVrEsEMMf3URQFVR9AAKt0ALSHPalpCaAPPfiWV1TxP4J0M8m51Brxs9CkCbiM9idw/I16EvSvMLDUh4l/aC1WGGbfb+GdHihnt5ExsuLlvMjkQ9wYkdT7jFenjpQAGvPvDzH/hcXizdwfsVrgeq7euPrkfhXoJrz7w8MfGLxZznNpan6fL939M/jQB6CKWkFLQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAZXinR38QeHtR01JzbPdQNEJRn5SR6AjNePx2XxAtvBuoWlr4A0m31bR9MXT9NuHu4JJL9gy/PEekUZC7ismDvK8HGT61401mfw94U1XU7VI5bm1tnliSXIQsBxnHOM1yNinj3xHpOmalBrGk6at1aRTtAtuZAGZQxwSPf9KAN74W6QdD8B6VZvo9xoUyq8k1jdXKXMqSvIzyM8sZKuzuzOSOMueB0HUlgK88/sP4iAf8jPpf0+xf8A1qw/EHgX4j+JnsgnxDj0y1t5S00WmWqRtckEYUykEqAQcheucEjFOw7HZ+IPiXpWjXkmn2qz61rCj/kH6anmyAnoHI4QcjJJ4BycDmse38I+IPHMTXHivULjS7Gfp4f06YKI0y3yy3CHLsQVJ2EYK8E5NU9L8D+MdCilTTNW0PT45ZDK62+nhdzE5JJ6t9Tk89avfD/W/EcnjHxHoWvXlnqH2BLeWCe2h8psOmWDDvzQB2mjaDp/h6wSy0yygsLSMkrDbxhFyTknA7nqT1PfNX1GBQowKWkIKKKKAELBetee6on/AAmHxWsbNcSaf4diNzcq2drXUi/uhjuVQ7uf+egIPBB6vxb4ms/B3h2/1m/LfZbOIyMsYy8h6KiDu7MVVR3LAVgfCHw/qGjeDre51tI18RamxvtTMROzz35IXPIUDAA7YxQB2yjArzr4tAHxD8MM4H/FUr1/7B97XooGBXnHxdONf+GHJH/FVL0/68L2gD0deBS0lLQAUUUUAFcv8Tjr6/D7xCfCuD4kFjKdPBAI8/adnXjrXUV5J8QLa+8RfGzwv4dXXtU0jS5fD2qX8sOmSpH5ssdzYIjMWVs4WaQYGPvUDRw0mu6T4M+EHxB1L4YXWu315a2cUkn2+eSVBeHeJNjz5CT4KmQfdX92cDPPpfwC8TDxD4C8l5dWnvdLunsrubWbuG8meXasuVuIQI5k2yqAydMFTyppZ/hGl2rpN4x8VSo42ur3sRBUg5BzF0OTxWRp3wn0Dw55eg2PjLXNM+zWxuF021u4IVhhDfM4jWIBV3HnAAyT3zTsOx6H4v8AE0HhXRJr6UGWXKxW9ugJeeZztjjUDnJbH0GSeAaz/APhibQdMkvNSbzte1FvtN/IcHY5/wCWSED7kY+VcDnGepNcND8FNG8V3Wk+I4PHXirUIYYnNlLFqaGL58fvVAQDdgFQ3oxpNf8AC954K8V+Cri08V+IrxLrVBBNbXl3G8MqFG4ZRGCRnngjmgR7KOlLSKMClpCCmt1FOrn/AB9qn9i+DNavQpcw2kjbVfYT8p6HsaAOI/Z8055dG8TeJZJPObxJr13qEQfmWGEEQpAxx/AYnwBwN3HU16sBtGK574daUdD8C6DZMMSRWcXmfLtJcqC5I9SxJPua6KgBD1rz7w5/yWLxcMY/0W1zx/sDnP6fhXoB61wHh/I+MXivcQT9itdp64XHT89x/GgD0AdKWkFLQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAct8UCB8PtfB4/0R/5VL4KP/FFeHf+wbb9f+ua1X+K08Nv8OvETzzLbx/YpB5jqzKDg4yF5xnGcV534Zg+O9n4b0q3+xfD2LybWKMRyz3wZQEAwfk6+vvTTsNOx6/eYNpOCruDG2Uj+8wx0HvXl/wRguY9T8WzLa6lZ6LNcQfYotShMLKQhEo2Ekk7sEvnDbvanMfjuQc2vw6PH/Pxf4/9ArK0/wAXfGXV/EWtaFb2fgEX2kpA1y0lxfbGEwZlA+TPRTn8OtO5XMe0ZA64ya4Pwrn/AIXR4zPb7HZAc/7BrIz8eD/y7fDof9vF/wD/ABFbHwz8K+MLDxBr2ueMn0MX1+Io4odCaZolRFxljKAd304xihsTdz0YdKWkHTmlqSQprNt7E/SnVU1TUbfSLC5vruUQ2ttE00sjdERQSzfgAaAOG8WEeLviJofh8jztO09P7WvUH3WdWxArf8C+bB9Aewr0JDketcL8KLC4k0i71+/jZNS1uc3cjPw3ldIRjsAmAB6Y713a0ALXnPxa/wCRg+GHGf8AiqV74/5h97Xo1ec/Fv8A5GD4YY4/4qle2f8AlwvaAPRQc0tIvFLQAUUUUAFeXa5/yct4SwMn/hEtZ6Dp/pmmV6jXE+NPhrD4p8TaX4gh1a/0jVdPtLixjls5dqtDM8LurDv80EeD2waaGjrCDx6cV55qHhPVpvjRN4gi022bSW8NSaabrzgJXmacOEZf7oCnn1k+tYHjTw1rukpaaXpXjfWLjxDqEgjto96t5CE4e5dT/wAs4xkkHG44UHJFXfFHgXXvD/gvU9QTx5rU17Z2LyiViAHkVCdxXoMkdKdx3Oi+DPh7UvCnwv0DRtWsIdO1CzhaKW2tn8yKP52wFbuMEVV+J/GveAP+w0nU/wCw1UPDPgHWtV8N6XezeOtbae5tY5nbcFyzKCeBwOtaNv8ACSaTXNI1HUfFGraoumXBuYrWaXETvtKguO+M5HuKTEz0QHNLSClpCCvPvjJm/wBH0jRFVpP7X1O3tZUQ4cwht7kHtgLnPYZNegV594ikOufFjw5pgIaLTYJdSkAOCrcxqf8Ax4D/AIEaBo7+PG3jp6U+moMD8adQIQ1594dCj4xeLQvObS1Lf720ZHvxt59zXoJrz7w8CPjF4tzxmztWGeMjaBn8wR+FAHoIpaSloAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAornvGnj/QPh7pyX3iDUU062kfYjFGkZjjJwqAsQAMk4wB1xWvaarZ38du9tdQ3C3EQnhMUgbzIyAQ64PKnI5HHNAFqkLAHBoBzWJ4y8UW3g7w/d6rdElIVwkSjc0shOERVHJJJAwKAOU8Rp/wALA+IFnoOSdF0PZqWofLkS3Gf9HhPsMGQ9c7QpGGr0Zelcx4B8NXHh3Q2F8ySateTPd30iElWlcjgE9lUIg9kFdOBgUABGTXm/gsf8Xp+JX/XHSu//AEylr0jvXnHgr/ktPxL/AOuOlf8AoqWgD0iiikLYoAWim7vY/lTqAEJxXnvxMJ8S6toHhJCWt7+U3WoIhw32aIg7Wx0Vn2jnghSK726uI7WGSWZhHEiF3duAqgckmuC+FFnLrSal4yvQ4vdblJgSTj7PaJxFEB27sexZiR1oA9AjUIgVQqqvAVRgCnCgDFLQAV5x8XMf8JB8MM4/5GlcZ/68L2vR684+LgJ8QfC/HX/hKl6/9eF7QB6MOntS0g6UFgPqaAFopu4f0oDg0AKTisDxp4vtfB2krdzpJcTTTR2ttawjLzzSOEjQemWYZboByava9rtn4c0ua/vpfKgjwOBlnY8KqgclicAAdTXPeFtButU1OTxHriMLx3b7BaueLOAgbQV6CX72489SBxnIBZ8GeEZdFlv9U1GZLzXdSk8y4nHzCNRwsMZIB8tccDA5JJ6074l5Hw78SgnP/Evn/wDQDXTgYFcz8Tj/AMW88S/9g6f/ANANAFjwISPBOgf9eEH/AKLWt4HNYPgU48E6B/14Qf8Aota3DIqKSxCgckntQA+iqem6vZazYRX2n3cF9ZTDdFc20iyRyDOMqwODz6VbBzQAhrzvwO6+IviR401tWEsFlJHosBK7WR41Dzj3BLR4P+ya76+uo7G1muJSRHChkYjqABk/pXFfBSzePwJFezLGLrU7q41CZkByzSSsQWJ6tt2j2wBzjNAHeL0paSloAQ1594dG34xeLOdwNpanjt8uNv6Z44+avQDxXn/h3afjD4t2ggC0tQx6/NtHI9BjAx6g0AegilppYL14oLgUAOopAQelLQAUUUmecd6AFooooAKKKKACiiigAooooAKKKKACiiigDzP4h6F4j0/xlpfizw5psHiOaCym02bR7q6FsAsjK3no7AjcuzaRjJV2xWD4S0C90f48pPL4duLRH8KwWV1qNhDs0vz45FIiiBfKhRuCjaOMZJxXc/Ebxtd+Do9GjsNL/ta91W+WxhhMwhVWKs25mPb5ayv+Eq+IOf8AkR7T1/5C8f8A8TQB6GDwefyrzm6hPxC+JkcJfd4f8Lus8iq+VudQIPlhgOohXL4P8bRkdOSfxV8RhBJ5PgeyM207N+sJt3Y4z8vTP/6qw/As3xE8K+HLezuPBdjPqEjPcXtymrx4mnclnb7oJGTgZ6KFHanYZ7Enyg59eKd1ry/V/iD440HS7vUbzwTbfZbWMzSiPV0LFR1wNp5r0TRNRTWNHsb+NDHHdwJOqt1AZQwB/OgC53rzjwV/yWn4l/8AXHSv/RUtej96848Ff8lp+Jf/AFx0r/0VLSEejivKfjrrd9YP4c06TWZvCvhbUZpo9Y8Q20vky2gVAYo1lIIh8xiQZDjAHUEivVs4rz3xf8QbdddvPDQ8Kah4lWO2SW7ENukkChycIwbqcDPTHI96AOB+H/xF1S2+KWj+F4fFA8U+Hbu3uI4r67hVC5gXcPKmAzcS4ZfMyAoGGUndge/g7R/hXj2nanZaRrsms2Xwr1S01N4VtzcQ2yKRGucKADgdcZAzit4/FLVR/wAyJr4/7Zr/AI07DsWPitePe2Wl+HLZ2W41y7W2k8s4kS2A3TOv0G0Z/wBuu2sbWKytIreBBFBCojjRRgKoGABXimleLPENz431LxBqngPX18lfselwgIwSHgvKcHhnOOOwFdcPijqo4/4QTX+v/PJf8aB2PQ6K5PwR8QE8ZXeq2j6TfaNe6c6JLb3yBXIZQysME8EGuspEi15z8WzjxD8L+SP+KpXocf8AMPva9Grzj4tnHiH4XkjP/FUr2z/y4XtAHoq8AV5J8a9XkHiLw7oep6/c+D/CF9Bcy3uvWl39jkFxGYvJt/tGQIg4aVs8Z8rbnnB9b6DH8q8t1/4laf4h1vxH4ZXwbqHiePRbuK0vlNqktv5rQRXCjDZzhJo+o6n2zQBzdp8WPFVn8QfBOjhrW98E6vp1u0fiq+sZI5NSuXR2MaBCqwOVRXCsmMbumMV7lNOlvE8sjiONQWZ3O0KB1JJ6cV41qt7HrXi2w8RXfgLxNJf2QHlx7v3BZd2xzGWwWTfJhsfxt61Prfjy/wDFM/8AZt98OPEFxo4CytMJYwkzhs+UyBslcgHng4xinYdjf8MCf4k6pbeKbyKa10exnl/sa1cFDN96M3UqnqGBPlg9FO7qRj0NOFwa87T4n6nGgVPAevqoHAEKgAdh1rQ8HfExPFfiTUtCm0XUtG1Cxtobt0vowoeOVnVSpB55jbIoCx21cx8Tj/xbzxL/ANg6f/0A10wORXM/E4/8W88S/wDYOn/9ANIRY8CnHgnQP+vCD/0WtYfxm8Oan4q8DXFlpcYu386KS405pfJGoWyuGmtd/wDD5qApk8c84rc8CnHgnQP+vCD/ANFrUXjvxlb+BdB/tO4tri9LzxW0VtagGSWSRwiKMkDqf/10xngXxV1G41r4aLJoGj+JfhRfaxren6Np11FKmn3BuJ5DEsk0Kbh5SNJkrkF+emM19L6dajT7C2tRLNOIY1j824ffI+ABuZj1Y4yT3Nef3HxGvrsIJ/h9rkwjdZFEkKMFdTlWGT1B6HtUw+KWrDj/AIQTxB/37X/GgLGj8YNZ/sH4beIL7Y7+XbHiN9jc8cH8a3vCulHQfDWlaYzI72VrFbs8a7VYqgBIHpkV5D8QvFGv+Lp/DVrH4D18adb6pHfXsqhAwWH50TaT86uw2MOwPeuv/wCFo6qB/wAiJr57/wCrX/GiwWPRKK5P4d/EOz+Ithqs9raXdhLpmoy6ZdW95HsdJowpYe4w6811lIQh61594eJPxi8WZxkWdqoA4+XbkfqTXoJrz7w+R/wuLxYF72lqWyejbRxj0xj9aAIfjp4j1Tw54UsW0+4fTbG71CO01XWYgC+l2bI5e5UHIyGEaZIO3zN3bI81ufjc3w2l8PabperP408NTXZt013UHkuJLp2mMX2SKeNSpki4Yyy/KykKCWyR6n4i+JiWniC/0C18Oanr728Km7NrErRrvGQhyeSVOfTFcR4g146qdKs5Php4rj0vS5N0Wn2ISGzmxgqHiUgMqlQVBGAadhnuinj1pc15YPjRrXI/4Vr4nJHUCOPI/DdR/wALn1r/AKJp4o/78x//ABVIR6nkUY5z36V5s/xinsrrTk1HwfrmnQ3t1FZi4mjXZG8hwpbngZ616SpzmgA6UtFFABRRRQAUUUUAFJnBxRnnFeU/GT9oDR/gve2Ca3HaJaXjWqJcT6pBblTLeQ2zEpIwbagmEhcZG2NwduMkA9VDhhkdKUHNeM/Df9qTwX4/vL61uNa0PRLqK6S1gtrjXbSWW4dhkKFVz83IUhSw3ZALYzU97+0jpem6Do183h/WdTvdc1BrPS9G0hI7i+uItlxIlwyM6BI2S1nYEtj5eCewB7BRXL/Dj4gWnxL8N/2xaafqOlBbma0msdVhWK5glico6OqswBDKehNdRQB5d8YtStLbxZ8MrOW4SO7uvEC+RC33pNkErPj6DmvR8N6H9a8b+N3geDxv8W/hQkt/eabPp9xf3dvcWMmx1f7My/lgmuk/4VZqGf8Ake/En/gSKtFoh8caxPpnxf8Ah1bLqN9Ba3v26Kayihke3mIhyjOwUqpVsYyR96vRgrehrzuX4Z3kGzzPH3iBBIwRRJdABmPQc9/QDrTx8LNQH/M9+JT9bkUahqbvxK+X4feIScj/AEN/5VoeAyB4I8P9B/xLrf8A9FLXmXxE+GOoQ+AvEMg8c+Iyy2UmCbkHB2nB/CrnhL4Y383hLQ5B448RRB7C3IRLngfulpCPXc815x4LP/F6fiV2/c6V/wCipaafhZqJ6ePPEmf+vgGsPRvhTZz69rl/pnxJ1281CRo7e/WDUEkMLRg7VdV+6cMeDzSsKx7LkVwGhMT8YvFfU/8AEvsiM9P+Wn+NVR8LNQx/yPniT8LkVxfh/wCG1/J8WPGEI8ceJAqWtn1uRwdhJbOO/p7U7WHax7t83uaxvGMkcfhnUWuJ7u1hWEs81mGMqAckgL8x4B6Zrlv+FWah/wBD34k5/wCnkVW1PwA+i2M19qHxG1yws4F3S3N1fLFFGPVmbAFMZL8Bb6/vvAkz3TXj266ldR2D3cLxlrQSEQlQ4D7NuMF/m9a9Gy3P3vXoa87h+GV7cQpNF4+8QyQyKGR47lSrKRwQR2NP/wCFW6hx/wAV14k9/wDSB/hQBJ4JI/4Wv8QvXzLLP/gOteig18/+D/hvqMvxL8ewN468RkRPZgZnA/5YA5yB7123/CrNQ5/4rzxL/wCBIpWFY9KzXnXxaVn8Q/DDaCceKVY7RngWF7mon+GN7GjM/j3xGqgFizXQAAHrWZqfwRHiSTSLu48c+I7g6ddC/s5I7wYWXynjDZHUbZX496VhWPWz/TvXk/wmJ/4Wj8bsZ/5GOz/9M+n1oj4WagX48d+JADgAC5HH6V538Nfh3eXXxD+LsSeL9et2g1+0DSR3GDKf7IseW9T/AICiw7HsfxH0KTxT8PfE+jJNdW76hplzarLZ/wCvQvGyho8/xDPHuBXLfA231Gz0jVLa806aztUuF+zXE9sbWS4G0biYskDBGMjrVn/hVt+M58d+JOAeTdcVlaH4asfE/n/2L8VtS1gQcS/YNUim8v8A3tpOPxpgergsQeCK890Y/wDGQvijnj/hHdN/9H3dL/wq2/5x478Sf+BNcFp3w4v3+PXiC2/4TTxCoj8O2DGQXPzMTcXPf2x+poGz6Grmfibz8PPEg9dPn/8AQDXOD4WagR/yPfiXp2uRWV4m+HEFto80OtfErW9PsrwfZTJd6gkIcuCAis2BuPYUrCsegeBD/wAUToHb/QIOv/XNa5H4+n/ildF5/wCZh0vkdR/pSc1FY/B+702wtrODx14lENvGsSBroE7VAAzx6CuL+M3w3vbLwtpbt438ROz67pqKzXAO0m5TBH507BY99yxJ69TXG/F3R31nwFqIEl/HJaAXkaafIySSsmSEyoJIPcd6ov8AC2/Lsf8AhOfEgyegueBVDWPBC+HbFr3VfiXrOlWSMFa5vr9IowScAFmwMnp1pjOu+H1hNpngTQbWWe5uZUsoy8t0SZWYrk7j1zk47V0ILFgDnk55rzbT/h9Jq1lFeWHxF129s5hujuLa8SSNx6hhwasf8Kt1AkAeO/EnX/n4FIVjP+ABxd/FH/sdb7n/ALZW9es5r5x+Dfw0u7mf4iGLxhr1pt8YXwbybjG/93Dyff3r0X/hVl+SB/wnXiXn/p5FKwWPSCa8+8PNn4xeLe3+iWgxnr8v3vxzj/gNc/ZeHLXU9cutHtfiZ4gl1G1GZYFuTkDvg4w2OM7Scd8VZtfgfLa6zeanF458Ti7vEjSUtdgghemBjinYLF/wtn/hc3jvGcfZ7Hv1/d8f5969C+YHPOPSvC/Afwz1DUfGvji9k8Z+IA6XsdmFF0QuxIxjpznnqTXef8KvvQcf8Jn4g/C7PT86AOD0rRvFlp8fZ44La8l0WG5mu7nVbhHRZopUDRwo27YyxsSmMbvlz3Fe9KRivJp9DsbTxHDoUvxE1qPVJV3JbG7fnI4G7oGPUKTk5yBW4vwuvcf8jp4gP/b0aQiL4zsHsPC1qAS1z4gs4wewILPz7fJj8a9DXpXg3xo8AXugeELHWk8W65Pd6ZrWmT24muSybnvIoW3KeoKSuMe+e1e8qNopCHUUUUAFFFFABRRRQB88/tT+GLDxZc6LZa3BeW+kBGcapBp51JYpt3EYtiCoLDkuynhQBjv4X8WINS8V/BL4Jjxlpb6reSWdp/aF1rN79iv4NRtl89vL/dNIJ5GgZBJ91VMqgBpVr74IOeKx9Z8GaJ4ileXU9Ltb+R7ZrRmuIw+6FvvJz2NAHy78EfC2nXnjttR1fT9HsriDTro6RFcW0KpNcXL273ShkVUbypoFH7vA3SSFRgjHjclj4YNn4K8Iz2vgXTm/4SVdSvLOW0u57Ag6dqSec8/yCSEOI1iSPaIyFBLZyf0FufBmiXdpplrNpdrJb6ZIktnG0YxAy/dKehFXJ9DsLmJI5LG2kjQbVV4VIVfQDtQB4t+xk2nw/CO+sdOl054bHxDqkBTSI3S1T/SndRErksFKurDJPDDmveKr2ljBYoUt4IrdSclYUCgn6D6D8qsUAeZePJ4oPjF8OWlkSMYv+XYD/l3PrXd/2jZEn/TbYc/89RVPxR4G0Pxp9l/trTYb/wCylmhaTIaMsMNtIIIyODWMPgt4MGf+JFCM+ksn/wAVVXKuc/8AF2wGtar4BubGwj1aXTtfguJbiKZAbKHDeZKckZGMAgc/MK9F/tGyyc31v9DKtc3/AMKY8GjpokQ/7ayf/FUD4L+Dcf8AIDi/7+yf/FUXC4nxL1Gz/wCFeeIsXlu3+hSdJV9PrVzwVqFn/wAIZ4fBvLdSNOt+DKP+ea1maj8CfA2q6fc2VzoEMttcxtFKhkk+ZCMEfep8HwP8E28MMS6DAFijWNP3knCqAAPvegFK4XOmnvrKS3lja7gcMhUoJgN2R0znivMfhDbxQavq19feH5vDN4oa1iWaSEQGESsVCbGO8nglmGegGAK6z/hS3gwHjQoRnriWTn/x6l/4Ux4NI50OI/WWQ/8As1FwudGNQsweb23P1lFcH4Z1K1Pxj8af6Zb4+yWX/LVeuw9s1sD4LeCxnGhQjJycSSf/ABVQj4F+BRcTXA8O2vnzALJLufcwH3QTu5Ap3C51f9o2f/P7b/jKK5zx9PaT+HZCtnFrksTrKltE8bSKRkB0VyFYrnOCQD60w/BPwURg6DD6f6yT/wCKp3/CmPBvX+w4gfaWT/4qi4XKXwd06Twp8M/D+karcWsOo2sBWZFnDYJYtz74IyOgNdj/AGhZnP8Aptv/AN/RXM/8KV8F7t39hQ59fNk/+Kpf+FLeCwSRoMGf+ukn/wAVRcLmR4O1G1X4qfEEm8twrNZEHzV/591HrXd/2jZYz9ttgPeUVy0XwL8CwXE08fh21jmnx5sis4Z8DAyd3NSD4K+CwMf2FCB6CWT/AOKouFzD+PPhy8+IXww1jQtD1azhu7mPJhklwt0oBJgYqQQHOAcdsg8Gt34Z3Elh8O/DVprDWun6nBYQxXNqJlxFIqAFRyeBj1pD8FvBhOf7Ch4GP9bJ0/76pf8AhS3gsgZ0OI4/6ayf/FUrhc6UalZKcm9t8A5P71a8w+FWoWq/Ev40lrqBVPiKzAJkGD/xKLA+tdX/AMKY8GjpocWf+usn/wAVUUfwO8DxPcOnh63V7hw8rK8gMjBQoLHdyQqqM+gFFwudLPe2U0MiG8tyHBXiYD9e1eS/s/8Ah278B2U2j3B+x6HY28FnZjUDbrckxjbw8QHmJtAwz/MTkkCu6/4Uv4M4/wCJHFx/01k/+KpD8F/BhIzocRx0zLIf/ZqdwudJ/aVlj/j+tv8Av6P8a860vULT/hofxMTdwBT4b0/B81ef9IuveuhPwW8GEAHQoiP+usn/AMVUY+BvgcXbXQ8PW4uGQRtKHk3FQSQud3QZP50XC51H9o2WP+P63/7+r/jXjf7QvhLUPF934YvtHmW8TT3nEtrB5Mokd48RmRJTtKBgCSPmHavQf+FMeDP+gHF/39k/+KoHwZ8Gg8aJGP8AtrJ/8VRcLo2tLvlTS7QXt5ZfbVhQT+TKNnmYG7b7ZziuE+Ot9aP4U0YC7gOPEOmEkSrgf6VH710B+C3gwqAdChI9PNk/+KqG5+BXgW8h8qbw5azRb1k2SM7DcpyrYLdQRwe1FwudY2o2W45vbcexlFcx8R9LsPFXhC/swum6leIpns4roo6LcKD5b4bIyD0pw+DHgzH/ACA4h9JZP/iqQ/Bjwacf8SOL/v7J/wDFUXC5b8FW2n+HvB+jaXHJa2gtLSKNoElXCNtG4dfXNbQ1GzDD/TLc/SUVzQ+C3gvOf7Chz6+ZJ/8AFUn/AApTwVzjQYM/9dJP/iqLhc5X4F6naef8Sw13CpHjS/X5nA5EcPFeoDUrIc/bbcjr/rV5/WuWg+B/ge2Mpi8P28ZllM0hR3G+Q4y7YbknA59ql/4Uv4MGP+JHFj2lkH/s1CYXRwngz4d32g/FTUNeutRszp7zXEyN9vLo4kChVihIAhYAfO4J38elevjUbJcf6bbH6SrXNH4LeDCCP7Chwev72T/4qk/4Up4LOM6DAccD95Jx/wCPUXHdGb8NdUsk8R+Owby3B/tgnHmr/wA809671tWsv+f23H1lWuPi+BXgSCaaaPw3axyzNvkZGcFz6n5uTU//AApjwZ/0A4h9JZP/AIqkTocJ4s+Hl9q3xhsNa0zVrWw8PSS2+o6ntul3XF1CjRKCm3IHl+UMhh9zkGvZV1axAP8Aplvx/wBNV/xrlf8AhTHg3PGhxe/72T/4qm/8KV8FndnQYTu6/vJP/iqA0MX9oPUrSX4X3CpdQsf7U0ngSA/8xK2969RBzXEf8KU8E5Unw/bNtdJAHZ2G5GDKcE4OGUEe4rtwMCkIWiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA//9k=" alt="" />
那我们求出每一个节点从1~左值的和 和 1~右值的和 他们的差就是这个节点的子树的所有的和(即这棵子树苹果数目)
可以百度下看看树状数组的实现
最后每输入一组数据就进行依次操作就可以了
#include <cstdio>
#include <cstring>
#include <vector>
#define MAXN 100005
#define mem(a) memset(a, 0, sizeof(a))
using namespace std; int TreeArray[MAXN], Left[MAXN], Right[MAXN], Fork[MAXN];
typedef vector<int> Ve;
vector<Ve>Edge(MAXN);
int N,M;
int key; void init()//初始化数组和
{
mem(Left); mem(Right);
mem(Fork); mem(TreeArray);
for(int i=;i<MAXN;i++)Edge[i].clear();
} void DFS(int node)//为每一个node添加一个左值和右值,表示这个节点所
{
Left[node] = key;
for(int i=;i<Edge[node].size();i++)
{
key+=;
DFS(Edge[node][i]);
}
Right[node] = key;
} int LowBit(int x)//返回的是2^k
{
return x & (x ^ (x-));
} void Edit(int k, int num)//修改节点k,如果是添加一个,代入1,删除一个代入-1
{
while(k <= N)
{
TreeArray[k] += num;
k += LowBit(k);
}
} int GetSum(int k)//得到1...k的和
{
int sum = ;
while(k>=)
{
sum += TreeArray[k];
k -= LowBit(k);
}
return sum;
} void ReadDataAndDo()
{
int a,b;
char ch;
for(int i=;i<N;i++)//输入a,b把边存放在容器里面
{
scanf("%d%d", &a, &b);
Edge[a].push_back(b);
}
key = ; DFS();//为每一个节点对应一个左边界和右边界,他自己就存放在左边界里面,而它的管辖范围就是左边界到右边界
for(int i=;i<=N;i++)
{
Fork[i] = ;//最初每个Fork上都有一个苹果
Edit(i,);//同时更新树状数组的值
}
scanf("%d%*c", &M);
for(int i=;i<M;i++)
{
scanf("%c %d%*c", &ch, &b);
if(ch == 'Q')//b的子树就是[Left[b], right[b]]
{
printf("%d\n", GetSum(Right[b]) - GetSum(Left[b]-));
}
else
{
if(Fork[b]) Edit(Left[b],-);//由于每个节点的编号就是它的左值,所以直接修改左节点
else Edit(Left[b],);
Fork[b] = !Fork[b];//变为相反的状态
}
}
} int main()
{
while(~scanf("%d", &N))
{
init();
ReadDataAndDo();
}
return ;
}
POJ3321 Apple Tree (树状数组)的更多相关文章
- POJ--3321 Apple Tree(树状数组+dfs(序列))
Apple Tree Time Limit: 2000MS Memory Limit: 65536K Total Submissions: 22613 Accepted: 6875 Descripti ...
- POJ3321 Apple Tree(树状数组)
先做一次dfs求得每个节点为根的子树在树状数组中编号的起始值和结束值,再树状数组做区间查询 与单点更新. #include<cstdio> #include<iostream> ...
- POJ 3321 Apple Tree(树状数组)
Apple Tree Time Limit: 2000MS Memory Lim ...
- POJ 3321:Apple Tree 树状数组
Apple Tree Time Limit: 2000MS Memory Limit: 65536K Total Submissions: 22131 Accepted: 6715 Descr ...
- E - Apple Tree(树状数组+DFS序)
There is an apple tree outside of kaka's house. Every autumn, a lot of apples will grow in the tree. ...
- POJ 3321 Apple Tree 树状数组+DFS
题意:一棵苹果树有n个结点,编号从1到n,根结点永远是1.该树有n-1条树枝,每条树枝连接两个结点.已知苹果只会结在树的结点处,而且每个结点最多只能结1个苹果.初始时每个结点处都有1个苹果.树的主人接 ...
- POJ 3321 Apple Tree (树状数组+dfs序)
题目链接:http://poj.org/problem?id=3321 给你n个点,n-1条边,1为根节点.给你m条操作,C操作是将x点变反(1变0,0变1),Q操作是询问x节点以及它子树的值之和.初 ...
- POJ 3321 Apple Tree 树状数组 第一题
第一次做树状数组,这个东西还是蛮神奇的,通过一个简单的C数组就可以表示出整个序列的值,并且可以用logN的复杂度进行改值与求和. 这道题目我根本不知道怎么和树状数组扯上的关系,刚开始我想直接按图来遍历 ...
- 3321 Apple Tree 树状数组
LIANJIE:http://poj.org/problem?id=3321 给你一个多叉树,每个叉和叶子节点有一颗苹果.然后给你两个操作,一个是给你C清除某节点上的苹果或者添加(此节点上有苹果则清除 ...
- HDU3333 Turing Tree 树状数组+离线处理
Turing Tree Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total ...
随机推荐
- Codeforces 435 A Queue on Bus Stop
题意:给出n队人坐车,车每次只能装载m人,并且同一队的人必须坐同一辆车,问最少需要多少辆车 自己写的时候想的是从前往后扫,看多少队的人的和小于m为同一辆车,再接着扫 不过写出来不对 后来发现把每一队的 ...
- HDU 1247 Hat’s Words (字符串匹配,暴力)
题意: 给出一堆单词,如果有一个单词可以分成左右串两个单词,并且在所给的一堆单词中存在,就是hat词,统计所有这样的词,并按字典序输出. 思路: 注意定义,一个hat词可以被两部分已经存在的词组成,那 ...
- erl_0012 timer:tc 测试模块函数调用运行耗时
timer:tc 可以测试出函数调用耗时,是erlang性能测试的好工具. timer:tc(?MODULE, Fun, [Args]).
- python练习程序(c100经典例7)
题目: 输出特殊图案,请在c环境中运行,看一看,Very Beautiful! for i in range(0,256): print('%c' % i),
- ecshop 调用指定分类的推荐,热卖,新品
未测试 1.includes/lib_goods.php文件.把SQL语句改一下,与category表关联即可 将 $sql = 'SELECT g.goods_id,g.goods_name, g. ...
- (六)6.10 Neurons Networks implements of softmax regression
softmax可以看做只有输入和输出的Neurons Networks,如下图: 其参数数量为k*(n+1) ,但在本实现中没有加入截距项,所以参数为k*n的矩阵. 对损失函数J(θ)的形式有: 算法 ...
- 【英语】Bingo口语笔记(19) - 如何用英语叙旧
- 【Python】入门 list有些不懂
# -*- coding: utf-8 -*- # -*- coding: cp936 -*- 首行加这个 代码里就可以加注释 raw_input("Press Enter Exit&quo ...
- Symfony2 学习笔记之内部构件
Symfony2内部是怎样工作的以及我们如何来扩展它呢?从外部整体上看,symfony2代码是由许多独立的层构成,每一层都是建立在前一层基础之上.其中,自动加载时不受框架直接管理的,它完全是在Univ ...
- 【LeetCode 236】Lowest Common Ancestor of a Binary Tree
Given a binary tree, find the lowest common ancestor (LCA) of two given nodes in the tree. According ...
