Pipe(点积叉积的应用POJ1039)

Pipe

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 9723		Accepted: 2964

Description

The GX Light Pipeline Company started to prepare bent pipes for the new transgalactic light pipeline. During the design phase of the new pipe shape the company ran into the problem of determining how far the light can reach inside
each component of the pipe. Note that the material which the pipe is made from is not transparent and not light reflecting.





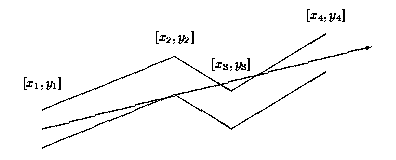
Each pipe component consists of many straight pipes connected tightly together. For the programming purposes, the company developed the description of each component as a sequence of points [x1; y1], [x2; y2], . . ., [xn; yn], where x1 < x2 < . . . xn . These
are the upper points of the pipe contour. The bottom points of the pipe contour consist of points with y-coordinate decreased by 1. To each upper point [xi; yi] there is a corresponding bottom point [xi; (yi)-1] (see picture above). The company wants to find,
for each pipe component, the point with maximal x-coordinate that the light will reach. The light is emitted by a segment source with endpoints [x1; (y1)-1] and [x1; y1] (endpoints are emitting light too). Assume that the light is not bent at the pipe bent
points and the bent points do not stop the light beam.

Input

The input file contains several blocks each describing one pipe component. Each block starts with the number of bent points 2 <= n <= 20 on separate line. Each of the next n lines contains a pair of real values xi, yi separated
by space. The last block is denoted with n = 0.

Output

The output file contains lines corresponding to blocks in input file. To each block in the input file there is one line in the output file. Each such line contains either a real value, written with precision of two decimal places,
or the message Through all the pipe.. The real value is the desired maximal x-coordinate of the point where the light can reach from the source for corresponding pipe component. If this value equals to xn, then the message Through all the pipe. will appear
in the output file.

Sample Input

4
0 1
2 2
4 1
6 4
6
0 1
2 -0.6
5 -4.45
7 -5.57
12 -10.8
17 -16.55
0

Sample Output

4.67
Through all the pipe.

Source

Central Europe 1995

题意:光线从(x0,uy0),(x0,y0-1)之间射入,向四面八方直线传播,问光线最远能射到哪里,或者能穿透整个通道.

思路:如果一条直线没有碰到一个端点,不是最优的,可以通过平移使之变成最优的,如果只碰到一个端点,也可以通过旋转使之交到两个端点,所以现在的任务就是枚举端点,找最大值

黑书(P359)

#include <set>
#include <map>
#include <list>
#include <stack>
#include <cmath>
#include <vector>
#include <queue>
#include <string>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const double eps = 1e-5;
const int INF = 0x3f3f3f3f;
struct node
{
    double x;
    double y;
}up[21],down[21]; //折点
int n;
int dblcmp(double p)//判断值的正负
{
    if(fabs(p)<=eps)
    {
        return 0;
    }
    return p<0?-1:1;
}

double det(double x1,double y1,double x2,double y2)//计算叉积
{
    return x1*y2-x2*y1;
}

double cross(node a,node b,node c)//计算a,b,c的有向面积;
{
    return det(b.x-a.x,b.y-a.y,c.x-a.x,c.y-a.y);
}

bool check(node a,node b,node c,node d)//判断线段ab与线段cd是否相交;
{
    return (dblcmp(cross(a,b,c))*dblcmp(cross(a,b,d)))<=0;
}

double Intersect(node a,node b,node c,node d)//计算相交的点的交点
{
    double area1=cross(a,b,c);
    double area2=cross(a,b,d);
    int c1=dblcmp(area1);
    int c2=dblcmp(area2);
    if(c1*c2<0)//如果小于零,规范相交
    {
        return (area2*c.x-area1*d.x)/(area2-area1);//计算交点的公式
    }
    else if(c1*c2==0)//和端点相交,判断和哪一个端点相交
    {
        if(c1==0)
        {
            return c.x;
        }
        else if(c2==0)
        {
            return d.x;
        }
    }
    return -INF;
}
int main()
{
    while(scanf("%d",&n)&&n)
    {
        for(int i=1; i<=n; i++)
        {
            scanf("%lf %lf",&up[i].x,&up[i].y);//上端点
            down[i].x=up[i].x;
            down[i].y=up[i].y-1;//下端点
        }
        bool flag=false;
        double Max_x=-INF;
        for(int i=1; i<=n; i++)
        {
            for(int j=1; j<=n; j++)
            {
                if(i!=j)
                {
                    int k;
                    for(k=1; k<=n; k++)
                    {
                        if(!check(up[i],down[j],up[k],down[k]))//计算光线的相交的管壁
                        {
                            break;
                        }
                    }
                    if(k>n)//光线通过了整个管道
                    {
                        flag=true;
                        break;
                    }
                    if(k!=1)//注意判断,1的时候不用处理,否则会WA;
                    {
                        double tmp=Intersect(up[i],down[j],up[k],up[k-1]);
                        if(Max_x<tmp)
                        {
                            Max_x=tmp;
                        }
                        tmp=Intersect(up[i],down[j],down[k],down[k-1]);
                        if(Max_x<tmp)
                        {
                            Max_x=tmp;
                        }
                    }
                }
            }
            if(flag)
            {
                break;
            }
        }
        if(flag)
        {
            printf("Through all the pipe.\n");
        }
        else
        {
            printf("%.2f\n",Max_x);//输出的是最大的x坐标,不是长度
        }
    }
    return 0;
}