Project Euler 104:Pandigital Fibonacci ends 两端为全数字的斐波那契数

Pandigital Fibonacci ends

The Fibonacci sequence is defined by the recurrence relation:

F[n] = F[n-1] + F[n-2], where F[1] = 1 and F[2] = 1.

It turns out that F541, which contains 113 digits, is the first Fibonacci number for which the last nine digits are 1-9 pandigital (contain all the digits 1 to 9, but not necessarily in order). And F2749, which contains 575 digits, is the first Fibonacci number for which the first nine digits are 1-9 pandigital.

Given that Fk is the first Fibonacci number for which the first nine digits AND the last nine digits are 1-9 pandigital, find k.

---

两端为全数字的斐波那契数

斐波那契数列由如下递归关系生成：

F[n] = F[n-1] + F[n-2], where F[1] = 1 and F[2] = 1.

可以发现，包含有113位数字的F541是第一个后9位数字是1至9全数字（包含1至9所有的数字，但不一定按照从小到大的顺序）的斐波那契数，而包含有575位数字的F2749是第一个前9位数字是1至9全数字的斐波那契数。

若Fk是第一个前9位数字和后9位数字都是1至9全数字的斐波那契数，求k。

解题

直接暴力，可取,时间过长，没有那么多时间跑

mathblog 算了下4.6天，完全不能容忍的

想到直接根据公式计算，但是也不是很好的，Mathblog中提到了，只求fib的第九位，判断是否是0-9的数

利用 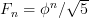，估算fib的值，或者说，当n很大的时候这个数和fib对于位的数是相等的，在题解中也看到好多都是根据这个思想计算的

其推到过程

Python
运行结果不对

不知道为什么

# coding=gbk

import time as time
import re
import math
import numpy as np
import math
def run():
    f1 = 1
    f2 = 1
    index = 1
    while True:
        f = (f1 + f2)%1000000000
        f1 = f2
        f2 = f
        index +=1
        if isPandigital(f):
            if first9(index):
                print index
                break

def first9(n):
    t = n *0.20898764024997873 -  0.3494850021680094
    last9 = int(10**(t - int(t)+8 ))
    return isPandigital(last9)
def isPandigital(s):
    if len(str(s)) !=9:return False
    return set(str(s)) == set('')

t0 = time.time()
run()
t1 = time.time()
print "running time=",(t1-t0),"s"