Python相关分析—一个金融场景的案例实操

哲学告诉我们：世界是一个普遍联系的有机整体，现象之间客观上存在着某种有机联系，一种现象的发展变化，必然受与之关联的其他现象发展变化的制约与影响，在统计学中，这种依存关系可以分为相关关系和回归函数关系两大类，本次分享，jacky将跟您分享如何用python做相关关系，并以真实金融案例为依托，深入浅出，探讨相关分析在实际工作中应用。

基础铺垫

• 相关系数（correlation coefficient）

  • 相关系数是变量间关联程度的最基本测度之一，如果我们想知道两个变量之间的相关性，那么我们就可以计算相关系数，进行判定。

• 相关系数基本特征

  • 方向

    • 正相关：两个变量变化方向相同

    • 负相关：两个变量变化方向相反

  • 量级（magnitude）

    • 低度相关：0 ≤ ｜r｜< 0.3

    • 中度相关：0.3 ≤ ｜r｜< 0.8

    • 高度相关：0.8 ≤ ｜r｜< 1

• 散点图

  • 在进行相关分析之前，通常会绘制散点图来观察变量之间的相关性，如果这些数据在二维坐标轴中构成的数据点分布在一条直线上的周围，那么就说明变量间存在线性相关关系，如下图所示：

如何用Python计算相关系数

计算公式

r=∑(ZXZY)N

• r：相关系数
• ZX：变量X的z分数
• ZY：变量Y的z分数
• N：X和Y取值的配对个数

金融场景案例实操

我们知道影响金融产品销量的因素很多，作为用户来讲，最直接的参考指标一定是产品的利率，金融机构为了吸引更多的用户能够持有或购买某项金融产品时，往往会推出加息活动，那么加息活动这个变量与实际销量之间是否存在相关关系？——下面jacky与您一同探讨与解决这个问题：

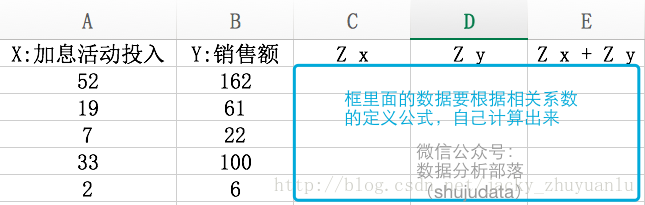
1.手工写代码计算相关系数

• 根据相关系数的计算公式，我们首先要计算出每个向量的z分数

  • z分数的计算公式：每个值减去向量的均值再除以标准差 ZX=(X-XMean)/XSD

#---author:朱元禄---
import numpy
X = [52,19,7,33,2]
Y = [162,61,22,100,6]

#均值
XMean = numpy.mean(X)
YMean = numpy.mean(Y)

#标准差
XSD = numpy.std(X)
YSD = numpy.std(Y)

#z分数
ZX = (X-XMean)/XSD
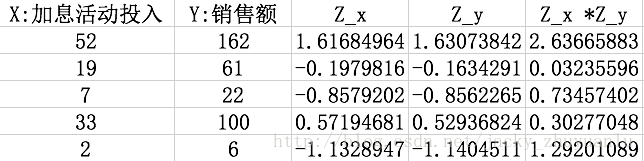
ZY = (Y-YMean)/YSD

• 根据上面相关系数的计算公司，我们套公式，手工计算一下

r=2.64+0.03+0.73+0.3+1.295=0.9997

• 也可以在python内直接计算：

#相关系数
r = numpy.sum(ZX*ZY)/(len(X))

2.使用numpy的corrcoef方法计算

numpy.corrcoef(X,Y)

• 我们可以看到用corrcoef计算的值和我们手工计算的值是一样的，这里计算得到的是一个对称矩阵，对角线的位置都是1，代表向量和本身完全自相关，1行2列和2行1列的值一样，因为第一个向量和第二个向量的相关系数等于第二个向量和第一个向量的相关系数，所以为对称矩阵

3.使用pandas.DataFrame的corr方法计算

import pandas
data = pandas.DataFrame({
'X':X,
'Y':Y
})
data.corr()

更深入的探讨：数据分析的陷阱－安斯库姆四重奏

相关系数是理解两个向量是否相关的非常好用的指标，但是在实际工作中，我们不能过分依赖相关系数，为什么这么说呢？因为统计指标是有局限性的。

1.Anscombe’s quartet

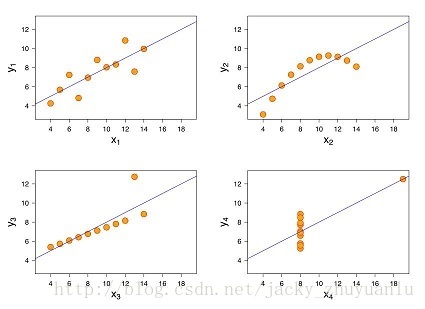
• 统计学里大名鼎鼎的Anscombe’s quartet是什么？（jacky有时真搞不懂统计学一些术语的翻译，quartet怎就翻译成了“四重奏”，既然得到了统计大佬们的公认，我也不好多说了）
• 先看下下面四个散点图，这四幅图表述的数据特征差异有对大，在散点图赏是不是一目了然？

• 下面我们来计算下它们的统计特性，竟然惊人的一样

性质	数值
X的平均数	9 （数据分析部落）
X的方差	11 （公众号：shujudata）
Y的平均数	7.5
Y的方差	4.12
X与Y之间的相关系数	0.816
线性回归线	y=3.00+0.500x

2.jacky解读

首先作为晚辈，要对统计学大师的学术成果表示尊敬与尊重。

但是，在时间工作中，Anscombe’s quartet的数据分析陷阱，作为一个合格的数据科学从业者，都是会规避的，首先我们做数据清理的时候，就规避了离群值对统计的影响，并且，随着机器学习，深入学习的发展，用方差，平均数来描述数据是最基本的，这些数据描述的维度是远远不够的。

数据科学的探索，永不止境，任何科学理论都可能被推翻。作为体制外的研究者，服务好我们的公司和客户，让数据真正的发挥商业价值，才是最重要的。在巨人的肩膀上，是你我的机会，更是这个时代留给我们最好的礼物！