R语言与概率统计(二) 假设检验
> ####################5.2
> X<-c(159, 280, 101, 212, 224, 379, 179, 264,
+ 222, 362, 168, 250, 149, 260, 485, 170)
> t.test(X,alternative='greater',mu=225,conf.level = 0.95)#单边检验 One Sample t-test data: X
t = 0.66852, df = 15, p-value = 0.257
alternative hypothesis: true mean is greater than 225
95 percent confidence interval:
198.2321 Inf
sample estimates:
mean of x
241.5
> ###########################5.3这是一个经典的两样本比较问题
> X<-c(78.1, 72.4, 76.2, 74.3, 77.4, 78.4, 76.0, 75.5, 76.7, 77.3)
> Y<-c(79.1, 81.0, 77.3, 79.1, 80.0, 79.1, 79.1, 77.3, 80.2, 82.1)
> t.test(X,Y,var.equal=TRUE,alternative='less')#常把我们想要的结果作为备胎h1 Two Sample t-test data: X and Y
t = -4.2957, df = 18, p-value = 0.0002176
alternative hypothesis: true difference in means is less than 0
95 percent confidence interval:
-Inf -1.908255
sample estimates:
mean of x mean of y
76.23 79.43 > t.test(X,Y,var.equal=F,alternative='less')#两组样本方差不同 Welch Two Sample t-test data: X and Y
t = -4.2957, df = 17.319, p-value = 0.0002355
alternative hypothesis: true difference in means is less than 0
95 percent confidence interval:
-Inf -1.9055
sample estimates:
mean of x mean of y
76.23 79.43 > t.test(X,Y,var.equal=TRUE,alternative='less',paired=T)#两组样本数量相同 Paired t-test data: X and Y
t = -4.2018, df = 9, p-value = 0.00115
alternative hypothesis: true difference in means is less than 0
95 percent confidence interval:
-Inf -1.803943
sample estimates:
mean of the differences
-3.2
#实战我们将使用MASS包中的UScrime数据集。它包含了1960年美国47个州的刑 罚制度
#对犯罪率影响的信息。我们感兴趣的结果变量为Prob(监禁的概率)、U1(14~24岁年龄
#段城市男性失业率)和U2(35~39岁年龄段城市男性失业率)。类别型变量So(指示该州是
#否位 于南方的指示变量)将作为分组变量使用 #如果你在美国的南方犯罪，是否更有可能被判监禁?
install.packages("MASS")
library(MASS)
attach(UScrime)
t.test(Prob~So)#默认原假设为监禁概率相同
detach(UScrime)
方差检验
> ################################5.5方差检验
> X<-c(78.1, 72.4, 76.2, 74.3, 77.4, 78.4, 76.0, 75.5, 76.7, 77.3)
> Y<-c(79.1, 81.0, 77.3, 79.1, 80.0, 79.1, 79.1, 77.3, 80.2, 82.1)
> var.test(X,Y,alternative='two.side') F test to compare two variances data: X and Y
F = 1.4945, num df = 9, denom df = 9, p-value = 0.559
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.3712079 6.0167710
sample estimates:
ratio of variances
1.494481
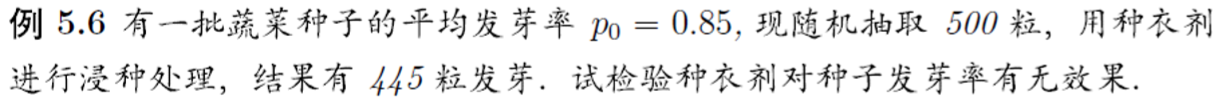
> ##############################5.6并非所有的样本总体都服从正态分布的假设！
> binom.test(445,500,p=0.85) Exact binomial test data: 445 and 500
number of successes = 445, number of trials = 500, p-value = 0.01207
alternative hypothesis: true probability of success is not equal to 0.85
95 percent confidence interval:
0.8592342 0.9160509
sample estimates:
probability of success
0.89
#######5.7
binom.test(1,400,p=0.01,alternative='less') ##################5.8拟合优度检验
X=c(210,312,170,85,223)
chisq.test(X)
length(X)
######################5.12单个总体的检验
X<-c(420, 500, 920, 1380, 1510, 1650, 1760, 2100, 2300, 2350)
ks.test(X, "pexp", 1/1500)
?ks.test ########################两个样本分布的比较
X<-rnorm(100)
Y<-runif(100) ks.test(X,Y)
t.test(X,Y)
wilcox.test(X,Y) #################################################5.14列联表的独立性检验
x<-c(60, 3, 32, 11)
dim(x)<-c(2, 2)
x
chisq.test(x, correct = FALSE)#一个逻辑指示在计算2乘2表时的测试统计量时是否应用连续性校正
#实际例子
install.packages("vcd")#关节炎治疗数据
help(package='vcd')
library(vcd)
help("Arthritis")
head(Arthritis)#查看列表的前几项
mytable=xtabs(~Treatment+Improved,data=Arthritis);mytable#创建一个列联表。接受治疗和改善水平之间有关系 chisq.test(mytable)
fisher.test(mytable)
#改善水平和性别的关系
mytable=xtabs(~Improved+Sex,data=Arthritis);mytable
chisq.test(mytable)
fisher.test(mytable)
#多维度列联表的检验;原假设是两变量在第三个变量的每一层中都是条件独立的
mytable=xtabs(~Treatment+Improved+Sex,data=Arthritis)
mantelhaen.test(mytable) #以上为独立性检验，如果变量独立，那么是否会相关呢？
library(vcd)#二维列联表相关性度量
mytable=xtabs(~Treatment+Improved,data=Arthritis);mytable
assocstats(mytable) ###############################5.22相关检验(相关性的度量)
x<-c(1,2,3,4,5,6); y<-c(6,5,4,3,2,1)
cor.test(x, y, method = "spearman")#还有person相关，kendall相关
实战
#实战
attach(state.x77)#基础包中的数据集，美国50个州在1977年的人口，收入，文盲率，预期寿命
#谋杀率，气温，土地面积等数据，我们想要判断预期寿命和谋杀率的关系
help(state.x77)
#install.packages("XQuartz");library(XQuartz);edit(state.x77);fix(state.x77)
head(state.x77)
states=state.x77[,1:6]#我们打算讨论除了气温和土地面积之外的所有变量的关系
cov(states)
cor(states)
pairs(state.x77)
cor.test(states[,4],states[,5])#预期寿命和谋杀率
detach(state.x77)
#cor.test 一次只能检验一对变量的相关性，而psych包中的corr.test()可以做的更多
library(psych)
corr.test(states,use='complete')#对所有变量做比较,prob 越小越显著
> states=state.x77[,1:6]#我们打算讨论除了气温和土地面积之外的所有变量的关系
> states
Population Income Illiteracy Life Exp Murder HS Grad
Alabama 3615 3624 2.1 69.05 15.1 41.3
Alaska 365 6315 1.5 69.31 11.3 66.7
Arizona 2212 4530 1.8 70.55 7.8 58.1
Arkansas 2110 3378 1.9 70.66 10.1 39.9
California 21198 5114 1.1 71.71 10.3 62.6
Colorado 2541 4884 0.7 72.06 6.8 63.9
Connecticut 3100 5348 1.1 72.48 3.1 56.0
Delaware 579 4809 0.9 70.06 6.2 54.6
Florida 8277 4815 1.3 70.66 10.7 52.6
Georgia 4931 4091 2.0 68.54 13.9 40.6
Hawaii 868 4963 1.9 73.60 6.2 61.9
Idaho 813 4119 0.6 71.87 5.3 59.5
Illinois 11197 5107 0.9 70.14 10.3 52.6
Indiana 5313 4458 0.7 70.88 7.1 52.9
Iowa 2861 4628 0.5 72.56 2.3 59.0
Kansas 2280 4669 0.6 72.58 4.5 59.9
Kentucky 3387 3712 1.6 70.10 10.6 38.5
Louisiana 3806 3545 2.8 68.76 13.2 42.2
Maine 1058 3694 0.7 70.39 2.7 54.7
Maryland 4122 5299 0.9 70.22 8.5 52.3
Massachusetts 5814 4755 1.1 71.83 3.3 58.5
Michigan 9111 4751 0.9 70.63 11.1 52.8
Minnesota 3921 4675 0.6 72.96 2.3 57.6
Mississippi 2341 3098 2.4 68.09 12.5 41.0
Missouri 4767 4254 0.8 70.69 9.3 48.8
Montana 746 4347 0.6 70.56 5.0 59.2
Nebraska 1544 4508 0.6 72.60 2.9 59.3
Nevada 590 5149 0.5 69.03 11.5 65.2
New Hampshire 812 4281 0.7 71.23 3.3 57.6
New Jersey 7333 5237 1.1 70.93 5.2 52.5
New Mexico 1144 3601 2.2 70.32 9.7 55.2
New York 18076 4903 1.4 70.55 10.9 52.7
North Carolina 5441 3875 1.8 69.21 11.1 38.5
North Dakota 637 5087 0.8 72.78 1.4 50.3
Ohio 10735 4561 0.8 70.82 7.4 53.2
Oklahoma 2715 3983 1.1 71.42 6.4 51.6
Oregon 2284 4660 0.6 72.13 4.2 60.0
Pennsylvania 11860 4449 1.0 70.43 6.1 50.2
Rhode Island 931 4558 1.3 71.90 2.4 46.4
South Carolina 2816 3635 2.3 67.96 11.6 37.8
South Dakota 681 4167 0.5 72.08 1.7 53.3
Tennessee 4173 3821 1.7 70.11 11.0 41.8
Texas 12237 4188 2.2 70.90 12.2 47.4
Utah 1203 4022 0.6 72.90 4.5 67.3
Vermont 472 3907 0.6 71.64 5.5 57.1
Virginia 4981 4701 1.4 70.08 9.5 47.8
Washington 3559 4864 0.6 71.72 4.3 63.5
West Virginia 1799 3617 1.4 69.48 6.7 41.6
Wisconsin 4589 4468 0.7 72.48 3.0 54.5
Wyoming 376 4566 0.6 70.29 6.9 62.9
> cov(states)
Population Income Illiteracy Life Exp Murder HS Grad
Population 19931683.7588 571229.7796 292.8679592 -407.8424612 5663.523714 -3551.509551
Income 571229.7796 377573.3061 -163.7020408 280.6631837 -521.894286 3076.768980
Illiteracy 292.8680 -163.7020 0.3715306 -0.4815122 1.581776 -3.235469
Life Exp -407.8425 280.6632 -0.4815122 1.8020204 -3.869480 6.312685
Murder 5663.5237 -521.8943 1.5817755 -3.8694804 13.627465 -14.549616
HS Grad -3551.5096 3076.7690 -3.2354694 6.3126849 -14.549616 65.237894
> cor(states)
Population Income Illiteracy Life Exp Murder HS Grad
Population 1.00000000 0.2082276 0.1076224 -0.06805195 0.3436428 -0.09848975
Income 0.20822756 1.0000000 -0.4370752 0.34025534 -0.2300776 0.61993232
Illiteracy 0.10762237 -0.4370752 1.0000000 -0.58847793 0.7029752 -0.65718861
Life Exp -0.06805195 0.3402553 -0.5884779 1.00000000 -0.7808458 0.58221620
Murder 0.34364275 -0.2300776 0.7029752 -0.78084575 1.0000000 -0.48797102
HS Grad -0.09848975 0.6199323 -0.6571886 0.58221620 -0.4879710 1.00000000
> cor.test(states[,4],states[,5])#预期寿命和谋杀率 Pearson's product-moment correlation data: states[, 4] and states[, 5]
t = -8.6596, df = 48, p-value = 2.26e-11
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.8700837 -0.6420442
sample estimates:
cor
-0.7808458 #所以是负相关
> corr.test(states,use='complete')#对所有变量做比较,prob 越小越显著
Call:corr.test(x = states, use = "complete")
Correlation matrix
Population Income Illiteracy Life Exp Murder HS Grad
Population 1.00 0.21 0.11 -0.07 0.34 -0.10
Income 0.21 1.00 -0.44 0.34 -0.23 0.62
Illiteracy 0.11 -0.44 1.00 -0.59 0.70 -0.66
Life Exp -0.07 0.34 -0.59 1.00 -0.78 0.58
Murder 0.34 -0.23 0.70 -0.78 1.00 -0.49
HS Grad -0.10 0.62 -0.66 0.58 -0.49 1.00
Sample Size
[1] 50
Probability values (Entries above the diagonal are adjusted for multiple tests.)
Population Income Illiteracy Life Exp Murder HS Grad
Population 0.00 0.59 1.00 1.0 0.10 1
Income 0.15 0.00 0.01 0.1 0.54 0
Illiteracy 0.46 0.00 0.00 0.0 0.00 0
Life Exp 0.64 0.02 0.00 0.0 0.00 0
Murder 0.01 0.11 0.00 0.0 0.00 0
HS Grad 0.50 0.00 0.00 0.0 0.00 0 To see confidence intervals of the correlations, print with the short=FALSE option
#以上大都是在讲两组比较，若是多组比较则需要方差分析的方法。这里仅介绍单因素方差分析
#多元方差分析参见《R语言实战》
#单因素方差分析中，你感兴趣的是比较分类因子定义的两个或多个组别中的因变量均值。以
#multcomp包中的cholesterol数据集为例(取自Westfall，Tobia，Rom，Hochberg，1999)，
#50 个患者均接受降低胆固醇药物治疗(trt)五种疗法中的一种疗法。其中三种治疗条件使用药
#物相同，分别是20 mg一天一次(1time)、10 mg一天两次(2times)和5 mg一天四次(4times)。
#剩下的两种方式(drugD和drugE)代表候选药物。哪种药物疗法降低胆固醇(响应变量)最多呢?
install.packages('multcomp')
library(multcomp)
attach(cholesterol)
head(cholesterol)
table(trt)
fit=aov(response~trt);summary(fit)#方差分析只能看出它们之间的不同，不能说明具体细节 #绘图表示细节
boxplot(response~trt)
install.packages('gplots')
library(gplots)
plotmeans(response~trt,xlab='Treatment',ylab='Response',main='difference between 5 treatment')
detach(cholesterol)
所有代码：
####################5.2
X<-c(159, 280, 101, 212, 224, 379, 179, 264,
222, 362, 168, 250, 149, 260, 485, 170)
t.test(X,alternative='greater',mu=225,conf.level = 0.95)#单边检验 ###########################5.3这是一个经典的两样本比较问题
X<-c(78.1, 72.4, 76.2, 74.3, 77.4, 78.4, 76.0, 75.5, 76.7, 77.3)
Y<-c(79.1, 81.0, 77.3, 79.1, 80.0, 79.1, 79.1, 77.3, 80.2, 82.1)
t.test(X,Y,var.equal=TRUE,alternative='less')#常把我们想要的结果作为备胎h1
t.test(X,Y,var.equal=F,alternative='less')#两组样本方差不同
t.test(X,Y,var.equal=TRUE,alternative='less',paired=T)#两组样本数量相同 #实战我们将使用MASS包中的UScrime数据集。它包含了1960年美国47个州的刑 罚制度
#对犯罪率影响的信息。我们感兴趣的结果变量为Prob(监禁的概率)、U1(14~24岁年龄
#段城市男性失业率)和U2(35~39岁年龄段城市男性失业率)。类别型变量So(指示该州是
#否位 于南方的指示变量)将作为分组变量使用 #如果你在美国的南方犯罪，是否更有可能被判监禁?
install.packages("MASS")
library(MASS)
attach(UScrime)
t.test(Prob~So)#默认原假设为监禁概率相同
detach(UScrime)
################################5.5方差检验
X<-c(78.1, 72.4, 76.2, 74.3, 77.4, 78.4, 76.0, 75.5, 76.7, 77.3)
Y<-c(79.1, 81.0, 77.3, 79.1, 80.0, 79.1, 79.1, 77.3, 80.2, 82.1)
var.test(X,Y,alternative='two.side') ##############################5.6并非所有的样本总体都服从正态分布的假设！
binom.test(445,500,p=0.85) #######5.7
binom.test(1,400,p=0.01,alternative='less') ##################5.8拟合优度检验
X=c(210,312,170,85,223)
chisq.test(X)
length(X)
######################5.12单个总体的检验
X<-c(420, 500, 920, 1380, 1510, 1650, 1760, 2100, 2300, 2350)
ks.test(X, "pexp", 1/1500)
?ks.test ########################两个样本分布的比较
X<-rnorm(100)
Y<-runif(100) ks.test(X,Y)
t.test(X,Y)
wilcox.test(X,Y) #################################################5.14列联表的独立性检验
x<-c(60, 3, 32, 11)
dim(x)<-c(2, 2)
x
chisq.test(x, correct = FALSE)#一个逻辑指示在计算2乘2表时的测试统计量时是否应用连续性校正 #实际例子
install.packages("vcd")#关节炎治疗数据
help(package='vcd')
library(vcd)
help("Arthritis")
head(Arthritis)#查看列表的前几项
mytable=xtabs(~Treatment+Improved,data=Arthritis);mytable#创建一个列联表。接受治疗和改善水平之间有关系 chisq.test(mytable)
fisher.test(mytable)
#改善水平和性别的关系
mytable=xtabs(~Improved+Sex,data=Arthritis);mytable
chisq.test(mytable)
fisher.test(mytable)
#多维度列联表的检验;原假设是两变量在第三个变量的每一层中都是条件独立的
mytable=xtabs(~Treatment+Improved+Sex,data=Arthritis)
mantelhaen.test(mytable) #以上为独立性检验，如果变量独立，那么是否会相关呢？
library(vcd)#二维列联表相关性度量
mytable=xtabs(~Treatment+Improved,data=Arthritis);mytable
assocstats(mytable) ###############################5.22相关检验(相关性的度量)
x<-c(1,2,3,4,5,6); y<-c(6,5,4,3,2,1)
cor.test(x, y, method = "spearman")#还有person相关，kendall相关 #实战
attach(state.x77)#基础包中的数据集，美国50个州在1977年的人口，收入，文盲率，预期寿命
#谋杀率，气温，土地面积等数据，我们想要判断预期寿命和谋杀率的关系
help(state.x77)
#install.packages("XQuartz");library(XQuartz);edit(state.x77);fix(state.x77)
head(state.x77)
states=state.x77[,1:6]#我们打算讨论除了气温和土地面积之外的所有变量的关系
cov(states)
cor(states)
pairs(state.x77)
cor.test(states[,4],states[,5])#预期寿命和谋杀率
detach(state.x77)
#cor.test 一次只能检验一对变量的相关性，而psych包中的corr.test()可以做的更多
library(psych)
corr.test(states,use='complete')#对所有变量做比较,prob 越小越显著 #以上大都是在讲两组比较，若是多组比较则需要方差分析的方法。这里仅介绍单因素方差分析
#多元方差分析参见《R语言实战》
#单因素方差分析中，你感兴趣的是比较分类因子定义的两个或多个组别中的因变量均值。以
#multcomp包中的cholesterol数据集为例(取自Westfall，Tobia，Rom，Hochberg，1999)，
#50 个患者均接受降低胆固醇药物治疗(trt)五种疗法中的一种疗法。其中三种治疗条件使用药
#物相同，分别是20 mg一天一次(1time)、10 mg一天两次(2times)和5 mg一天四次(4times)。
#剩下的两种方式(drugD和drugE)代表候选药物。哪种药物疗法降低胆固醇(响应变量)最多呢?
install.packages('multcomp')
library(multcomp)
attach(cholesterol)
head(cholesterol)
table(trt)
fit=aov(response~trt);summary(fit)#方差分析只能看出它们之间的不同，不能说明具体细节 #绘图表示细节
boxplot(response~trt)
install.packages('gplots')
library(gplots)
plotmeans(response~trt,xlab='Treatment',ylab='Response',main='difference between 5 treatment')
detach(cholesterol)
R语言与概率统计(二) 假设检验的更多相关文章
- R语言结合概率统计的体系分析---数字特征
现在有一个人,如何对这个人怎么识别这个人?那么就对其存在的特征进行提取,比如,提取其身高,其相貌,其年龄,分析这些特征,从而确定了,这个人就是这个人,我们绝不会认错. 同理,对数据进行分析,也是提取出 ...
- R语言与概率统计(一) 描述性统计分析
#查看已安装的包,查看已载入的包,查看包的介绍 ########例题3.1 #向量的输入方法 w<-c(75.0, 64.0, 47.4, 66.9, 62.2, 62.2, 58.7, 6 ...
- R语言与概率统计(六) 主成分分析 因子分析
超高维度分析,N*P的矩阵,N为样本个数,P为指标,N<<P PCA:抓住对y对重要的影响因素 主要有三种:PCA,因子分析,回归方程+惩罚函数(如LASSO) 为了降维,用更少的变量解决 ...
- R语言与概率统计(五) 聚类分析
#########################################0808聚类分析 X<-data.frame( x1=c(2959.19, 2459.77, 1495.63, ...
- R语言与概率统计(四) 判别分析(分类)
Fisher就是找一个线L使得组内方差小,组间距离大.即找一个直线使得d最大. ####################################1.判别分析,线性判别:2.分层抽样 #inst ...
- R语言与概率统计(三) 多元统计分析（下）广义线性回归
广义线性回归 > life<-data.frame( + X1=c(2.5, 173, 119, 10, 502, 4, 14.4, 2, 40, 6.6, + 21.4, 2.8, 2. ...
- R语言与概率统计(三) 多元统计分析（中）
模型修正 #但是,回归分析通常很难一步到位,需要不断修正模型 ###############################6.9通过牙膏销量模型学习模型修正 toothpaste<-data. ...
- R语言与概率统计(三) 多元统计分析（上）
> #############6.2一元线性回归分析 > x<-c(0.10,0.11,0.12,0.13,0.14,0.15,0.16,0.17,0.18,0.20,0.21,0. ...
- R语言基础入门之二：数据导入和描述统计
by 写长城的诗 • October 30, 2011 • Comments Off This post was kindly contributed by 数据科学与R语言 - go there t ...
随机推荐
- JSONObject fromObject() 需要引入的包
1. maven项目 在pom.xml中添加以下依赖: <dependency> <groupId>net.sf.json-lib</groupId> <ar ...
- java—锁的学习研究
摘抄自博客:https://www.cnblogs.com/qifengshi/p/6831055.html 标题:Java中的锁分类 锁的分类: 公平锁/非公平锁 可重入锁 独享锁/共享锁 互斥锁/ ...
- 【Codeforces】Orz Panda Cup
大大出的题 大大经常吐槽没有人补,所以我决定做一个 A. APA of Orz Pandas 题意:给你一个包含+-*/%和()的表达式,让你把它转化成java里BigInteger的形式 大概就像这 ...
- python改成了python3的版本，那么这时候yum就出问题了
既然把默认python改成了python3的版本,那么这时候yum就出问题了,因为yum貌似不支持python3,开发了这个命令的老哥也不打算继续写支持python3的版本了,所以,如果和python ...
- Eclipse断点种类
本文是Eclipse调试(1)——基础篇 的提高篇.分两个部分: 1) Debug视图下的3个小窗口视图:变量视图.断点视图和表达式视图 2) 设置各种类型的断点 变量视图.断点视图和表达式视图 1. ...
- SpringBoot + Maven + Hibernate ( 简单实现CRUD功能 )
工具:idea.mariadb数据库 创建一个项目 ( student ) ........(使用idea创建一个springboot项目,这里我就不多说了) Maven 中的依赖 <?xml ...
- stm32——modbus例程网址收藏
https://blog.csdn.net/baidu_31437863/article/details/82178708 STM32(五) Modbus https://blog.csdn.net/ ...
- pypdf2:下载Americanlife网页生成pdf合并pdf并添加书签
初步熟悉 安装 pip install pypdf2 合并并添加书签 #!/usr/bin/env python3.5 # -*- coding: utf-8 -*- # @Time : 2019/1 ...
- React组件式编程Demo-用户的增删改查
1.项目结构 项目是基于webpack4, 参考 创建基本的webpack4.x项目 2.页面效果 初始化效果
- ajax+批量下载文件
用过浏览器的开发人员都对大文件上传与下载比较困扰,之前遇到了一个php文件夹上传下载的问题,无奈之下自己开发了一套文件上传控件,在这里分享一下.希望能对你有所帮助.此控件PC全平台支持包括mac,li ...