LNOI2018 劈配

主要思路为连反向边。

对于本题，贪心策略，依次决定每个人的最优解

但因为每人达到的最优解可能有多种方式，如果每个都尝试就会超时，所以只能先采取其中一种

并将这个方案连反向边，其它方案连正向边

这样对于之后的人决策，可以看哪些导师能够走到汇点

就是反向建图后，从汇点BFS判断能到达哪些导师，再判断哪个更优。

例如：对于这个例子

建图为

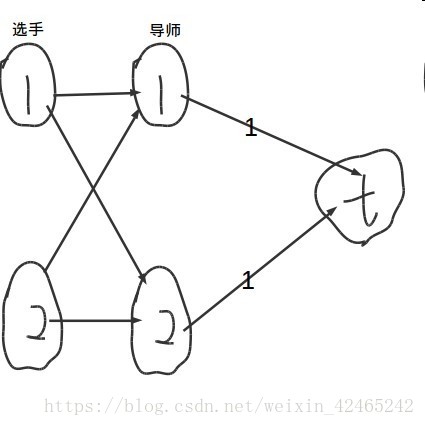
先考虑选手1。 1，2号导师都能到达汇点，并且选择1，2号导师对于目前来说都是最优解(现在无法确定哪个对于之后更优)，所以先选择1。

图变为

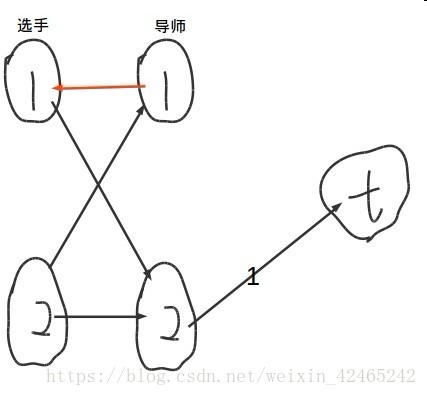
（红色为反向边）

考虑选手2。 1，2号导师都能到达汇点，1更优，所以选择1。这里走了反向边后走到了2导师，相当于让1选手选择2导师。

这个思想类似最大流的增广路算法（都是利用反向边来调整之前错误的决策）。

这道题有“前 i 名的录取结果最优，当且仅当在前 i − 1 名的录取结果最优的情况下：第 i 名 被其理论可能的最高志愿录取”这句话，这个属于贪心。这有这样，才能使用本题思想。

#include <stdio.h>
int fr[410],ne[5010],lad[410];
int v[5010],w[5010],bs=0;
int dl[410],la[410],n,m,sy[210];
bool bk[410],xz[210][210];
int zy[210][210],jg[210],yq[210];
void addb(int a,int b,int c)
{
    v[bs]=b;
    w[bs]=c;
    ne[bs]=fr[a];
    fr[a]=bs;
    bs+=1;
}
void bfs()
{
    for(int i=1;i<=n+m;i++)
        bk[i]=false;
    int he=0,ta=0;
    for(int i=1;i<=m;i++)
    {
        if(sy[i]>0)
        {
            dl[ta]=i+n;
            la[i+n]=-1;
            bk[i+n]=true;
            ta+=1;
        }
    }
    while(he<ta)
    {
        for(int i=fr[dl[he]];i!=-1;i=ne[i])
        {
            if(w[i]>0&&!bk[v[i]])
            {
                bk[v[i]]=true;
                dl[ta]=v[i];
                la[v[i]]=i;
                lad[v[i]]=dl[he];
                ta+=1;
            }
        }
        he+=1;
    }
}
void jisuan()
{
    for(int i=1;i<=n;i++)
    {
        bfs();
        for(int j=1;j<=m;j++)
            xz[i][j]=bk[n+j];
        int t=-1;
        for(int j=1;j<=m;j++)
        {
            if((bk[n+j]&&zy[i][j]>0)&&(t==-1||zy[i][j]<zy[i][t]))
                t=j;
        }
        if(t==-1)
        {
            jg[i]=m+1;
            continue;
        }
        jg[i]=zy[i][t];
        int x=t+n;
        while(1)
        {
            if(la[x]==-1)
            {
                sy[x-n]-=1;
                break;
            }
            w[la[x]]-=1;
            w[la[x]^1]+=1;
            x=lad[x];
        }
        for(int j=1;j<=m;j++)
        {
            if(zy[i][j]==zy[i][t])
            {
                if(j==t)
                {
                    addb(i,j+n,1);
                    addb(j+n,i,0);
                }
                else
                {
                    addb(j+n,i,1);
                    addb(i,j+n,0);
                }
            }
        }
    }
}
int main()
{
    int T,C;
    scanf("%d%d",&T,&C);
    while(T--)
    {
        bs=0;
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n+m;i++)
            fr[i]=-1;
        for(int i=1;i<=m;i++)
            scanf("%d",&sy[i]);
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
                scanf("%d",&zy[i][j]);
        }
        for(int i=1;i<=n;i++)
            scanf("%d",&yq[i]);
        jisuan();
        for(int i=1;i<=n;i++)
            printf("%d ",jg[i]);
        printf("\n");
        for(int i=1;i<=n;i++)
        {
            int l=0,r=i;
            while(l<r)
            {
                int mi=(l+r)>>1;
                bool zd=false;
                for(int j=1;j<=m;j++)
                {
                    if(xz[i-mi][j]&&zy[i][j]!=0&&zy[i][j]<=yq[i])
                    {
                        zd=true;
                        break;
                    }
                }
                if(zd)
                    r=mi;
                else
                    l=mi+1;
            }
            printf("%d ",l);
        }
        printf("\n");
    }
    return 0;
}