S02_CH16 等精度频率计实验

在了解了AXI总线之后，今天我们自己动手设计一个带AXI4-Lite总线的IP，来完成频率计的实验。

频率计虽然小，但是也算五脏俱全，涉及到zynq的方方面面，比如：

A）PL部分逻辑设计

B）自定义AXI4-Lite的IP的建立

C）通过AXI4-Lite总线实现PS与PL间的数据传递

D）PS控制输入输出外设

16.1等精度频率计原理

16.1.1引言

传统的数字频率测量方法有脉冲计数法和周期测频法，但这两种方法分别适合测量高频和低频信号，具有较大的局限性。多周期同步测频法以脉冲计数法为基础，并对之进行改进，实现了全频段的等精度测量，且测量精度大大提高，因此多周期同步测频法在目前测频系统中得到越来越广泛的应用。很多文献对多周期同步测频法的等精度测量原理有所介绍，但多数文献都是从测频控制模块的结构和测频波形出发，对测频原理进行论述。就我的亲身感触而言，这种阐述方式并不能帮助读者很快很好地理解频率计的原理（也有可能是本人比较笨>_<），因此，本文以脉冲计数法为基础，对之进行逐步改进得到多周期同步测频法，即等精度测频法，个人觉得这种逐步深入的方法可以更好地理解等精度频率计的原理。

16.1.2频率测量原理

所谓频率，就是周期性信号在单位时间内变化的次数。频率测量的方法有很多种，在模拟电路中有比较测频法，响应测频法，游标法等；在数字电路中，有基于脉冲计数测频原理的直接测频法、周期测频法、在直接测频法的基础上发展起来的多周期同步测频法和全同步数字测频法。本小节简单介绍计数测频法和周期测频法，重点分析多周期同步测频法的工作原理。

16.1.3脉冲计数法

脉冲计数法原理：在预置的闸门时间Tpr内对被测脉冲信号进行计数，得到脉冲数Nx，通过公式Fx=Nx/Tpr可计算出单位时间内脉冲个数，即被测信号的频率。

该方法测量误差来源于闸门时间Tpr和计数值Nx，且被测信号频率Fx与闸门开启时间Tpr越大，测频精度越高。因此，该方法适合于高频率信号的测量。

16.1.4 周期测频法

预置测频闸门开启时间Tpr等于被测信号的周期Tx，通过计数器在闸门时间Tpr内基准时钟信号进行计数，若得到的基准时钟信号脉冲个数为Nx，且基准时钟周期为T，则可按公式Tx=T*Nx计算出待测信号的周期Tx，然后换算得到被测信号频率。

该方法的测量误差来源于基准时钟信号和计数误差，且测量相对误差与被测频率Fx成正比，与基准时钟频率F成反比。所以，当被测信号频率越低，基准时钟频率越高时，周期测频法的测量精度越高。

16.1.5多周期同步测频原理及误差分析

用范围，但不能兼顾高低频等精度的测量要求。多周期同步频率测量法以脉冲计数测频法为基础，实现了闸门信号与被测信号的同步，从而解决了上述问题，实现了测量全频段的等精度测量。

从脉冲计数测频法原理可以看出，该方法闸门信号与被测信号不同步，也就是说在时间轴上两路信号随机出现，相对位置具有随机性。因此即使在相同的闸门时间内，被测脉冲计数结果也不一定相同，闸门时间大于N*Ttestclk时，越接近(N+1)*Ttestclk，误差越大。为了解决这个问题，利用D触发器使闸门信号在被测信号的上升沿产生动作，这样以来测量的实际门控时间刚好是被测信号周期的整数倍，这样就消除了被测信号引起的1个周期的误差。

这里还是给个时序图，解释一下引入D触发器为何能消除被测信号引起的1个周期的误差。

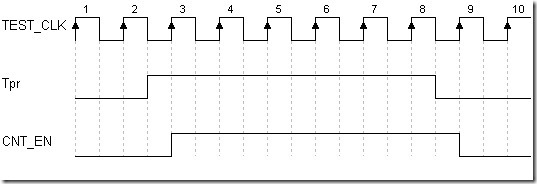
图1 Tpr处理后成为CNT_EN

由于引入了D触发器，CNT_EN不会在Tpr发生变化时立即变化，而是在TestClk上升沿到来时才发生变化，从而保证CNT_EN刚好是TEST_Clk的整数倍。测频法和测周法的原理和误差分析如果不明白，自己画个图试试，可以很好地帮助理解。

解决问题的同时，产生了新的问题：实际闸门时间与预置闸门时间不相等，因此需要获取实际闸门时间。为解决这一问题，引入另一计数器和标准时钟信号。在测量被测信号频率的同时，对标准时钟脉冲进行计数，通过计算即可得到实际闸门时间。这样就得到多周期同步频率计的主要结构，如图2所示。

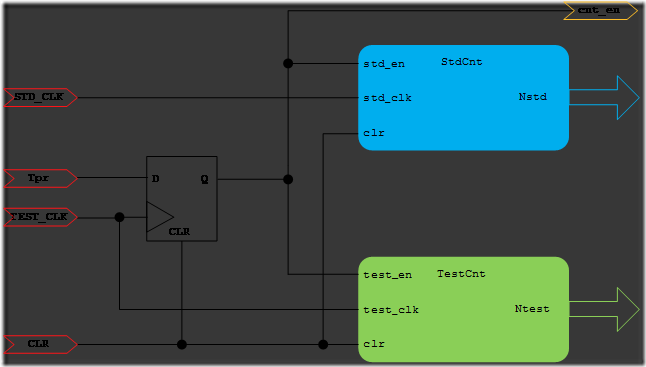
图2 测频主控模块结构图

其中，STD_CLK为标准时钟；Tpr为预置门控信号；TEST_CLK为待测信号；CLR为计数清零信号。

在计数允许时间内，同时对标准信号和被测信号进行计数，由于两个计数器计数时间相等，从而得到公式（1）。

Nstd/Fstd=Ntest/Ftest 公式(1)

其中Nstd为标准时钟计数值；Fstd为标准时钟频率；Ntest为待测信号计数值；Ftest为待测信号频率，由公式（1）可知待测频率为Ftest=Fstd*Ntest/Nstd。

由于未对标准时钟进行同步计数，所以测量结果会产生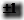个标准信号脉冲的误差。

从以上论述可以得出如下结论：

待测信号频率Ftest的相对测量误差与待测信号频率无关。

增大Tpr或提高Fstd，可以增大Nstd，减少测量误差，提高测量精度。

标准频率误差为△Fstd/Fstd。测试电路可采用高频率稳定度和高精度的恒温可微调的晶体振荡器作标准频率发生电路从而进一步降低测频误差。

16.2等精度频率计设计

16.2.1 PS寄存器功能划分

reg0：控制寄存器0（offset：0x00）

Bit	功能
Bit31~bit2	保留
Bit1	闸门信号Tpr（高时打开闸门）
Bit0	复位/清零信号clr（低有效）

reg1：数据寄存器Nstd（offset：0x04）

Bit	功能
Bit31~bit0	标准时钟计数值

reg2：数据寄存器Ntest（offset：0x08）

Bit	功能
Bit31~bit0	待测信号计数值

16.2.2具体实现

本文方案实现亦分为两部分，一是计数值的获取，该部分由测频控制模块（PL实现）完成；二是结果的计算及显示，该部分工作由PS完成。采用Miz系列开发板板载的100MHz时钟信号作为标准信号，可使测量的最大相对误差小于或等于10^-8。

16.2.3频率计PL部分代码设计

测频主要控制部分结构图在原理篇已经给出，该结构并不复杂，且所用元件较为常见。因此可以自行编码实现，也可以调用元件库实现。

这部分涉及到创建基于AXI4-Lite总线的IP核，方法参见前面章节内容

根据之前的分析，PL部分我们需要在闸门型号打开时，我们需要对标准时钟StdClock以及待测时钟TestClock分别进行计数。闸门信号关闭时停在计算，并把计数值存放到寄存器中等待PS通过AXI4-Lite总线读取数据。

在自定义AXI4-Lite IP内部添加用户逻辑如下：

reg clr;

reg Tpr;

reg[31:0] Nstd;

reg[31:0] Ntest;

reg [11:0]rlcd_rgb;

always @( posedge S_AXI_ACLK )

begin

if ( S_AXI_ARESETN == 1'b0 )

begin

clr <= 1'd0;

Tpr <= 1'd0;

end

else

begin

clr <= slv_reg0[0];

Tpr <= slv_reg0[1];

end

always @(posedge S_AXI_ACLK)

if(clr == 1'b0)

begin

Nstd <= 32'd0;

end

else if(Tpr == 1'b1)

begin

Nstd <= Nstd + 1'b1;

end

else

begin

Nstd <= Nstd;

end

//------------------------------

always @(posedge FRE_i)

if(clr == 1'b0)

begin

Ntest <= 32'd0;

end

else if(Tpr == 1'b1)

begin

Ntest <= Ntest + 1'b1;

end

else

begin

Ntest <= Ntest;

end

// User logic ends

这里的测试时钟是FRE_i，后续我们可以观察PS那边计算的结果。

16.3硬件工程搭建

本章工程比较简单，在上一章AXI_OLED的工程的基础上添加一个上一节封装的IP和用PS端输出一个测试时钟即可，完成的硬件工程如下图所示：

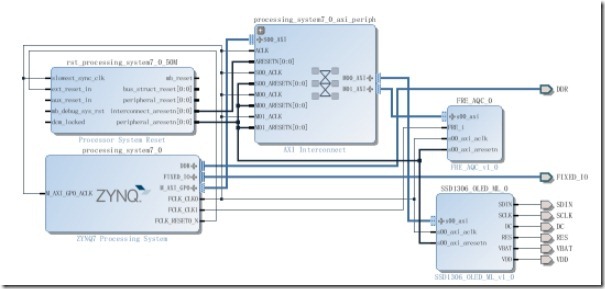
完善工程后，生成Bit文件即可。

16.4 导入到SDK

Step1:导出硬件。

Step2:用以下程序替换之前main.c中的内容。

* main.c

* Created on: 2016年7月1日

* Author: Administrator

#include <stdio.h>

#include"xbasic_types.h"

#include "OLED.h"

#include "sleep.h"

#include "xparameters.h"

void print(char *str);

#define FRE_AQC_BASE XPAR_FRE_AQC_0_BASEADDR

int main()

{

char str[16]="";

u32 fre_std,fre_test;

double fre_val;

oled_fresh_en();//enable oled print

print_message("frequency test",0);

while(1)

{

Xil_Out32(FRE_AQC_BASE,0);

usleep(10);

Xil_Out32(FRE_AQC_BASE,3);

usleep(100000);

fre_std =Xil_In32(FRE_AQC_BASE+4);

fre_test =Xil_In32(FRE_AQC_BASE+8);

fre_val =(double)fre_test/fre_std*100;

sprintf(str,"f=%.4lfMHZ",fre_val);

print_message(str,1);

Xil_Out32(FRE_AQC_BASE,0);

usleep(10);

Xil_Out32(FRE_AQC_BASE,3);

usleep(1000);

fre_std =Xil_In32(FRE_AQC_BASE+4);

fre_test =Xil_In32(FRE_AQC_BASE+8);

fre_val =(double)fre_test/fre_std*100;

sprintf(str,"f=%.4lfMHZ",fre_val);

print_message(str,2);

sleep(1);

}

return 0;

}

Step3：右击工程，选择Debug as ->Debug configuration。

Step4：选中system Debugger,双击创建一个系统调试。

Step5：设置系统调试。

Step6:单击运行程序按钮运行程序，此时可在OLED上观察到测量的频率值。

16.5 误差分析

单击运行程序后，在OLED上我们看到测得的频率为23.6M，此时查看ZYNQ Processing System的输出频率为23MHZ，实际为23.2558，基本满足功能要求。

16.6 本章小结

计算在PS部分进行很简单，就是一个除法，成功的关键在于AXI总线通信无误。

通过本章的学习主要是培养读者设计IP的思路，如何划分寄存器功能。以及如何将任务合理的分配给PL以及PS，让其发挥各自的优势。