【线段树】【P5522】[yLOI2019] 棠梨煎雪

C [yLOI2019] 棠梨煎雪

Background

岁岁花藻檐下共将棠梨煎雪

自总角至你我某日辗转天边

天淡天青 宿雨沾襟

一年一会信笺却只见寥寥数言

——银临《棠梨煎雪》

Description

给定 \(m\) 个长度为 \(n\) 的可能含有 ？ 的 01 串，其中 ? 既能代表 0 也能代表 1， \(q\) 次操作，每次给定一个区间，求有多少 01 串满足区间内的所有字符串都可以解释成该 01 串，或者单点修改某个字符串。

Limitations

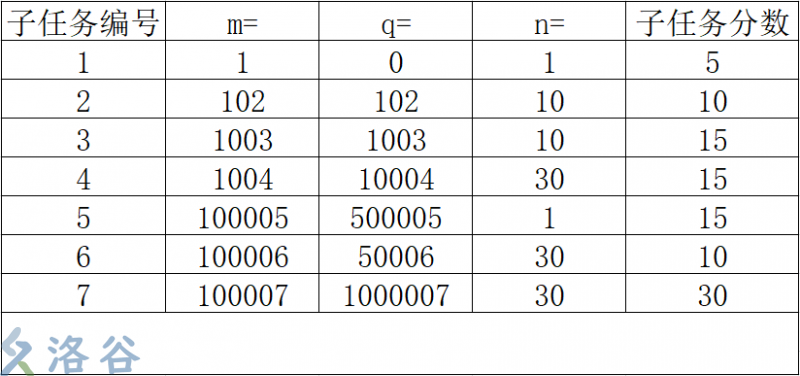
Solution

子任务 \(1\)：

输出 \(0\) 即可得分，期望得分 \(5~pts\)。

子任务 \(2\)：

考虑 \(n\) 只有 \(10\)，因此可以 \(O(2^n)\) 去枚举所有可能的串，然后对于每个询问 \(O(m)\) 的逐个判定是否合法。时间复杂度 \(O(qm2^n)\)，期望得分 \(10~pts\)。

子任务 \(3\)：

考虑对于一段所有字符串的第 \(x\) 个字符，一共有四种可能：确定为 \(0\)；确定为 \(1\)；都可以；都不可以。如果 \(0/1\) 都不可以，则答案为 \(0\)，因为不会有任何一个字符串匹配该区间。如果确定为某个数，则这一位只有一种可能；否则这一位有两种可能。根据乘法原理，如果有 \(a\) 个位置有两种可能，则本次询问的答案为 \(2^a\)。

因此对于每个询问，\(O(nm)\) 地去遍历区间内所有字符即可。时间复杂度 \(O(nmq)\)，期望得分 \(15~pts\)。

子任务 \(4\)：

考虑 \(n\) 只有 \(30\)，可以状压到 int 中。具体的，维护两个 int，第一个 int 维护对应位是否确定是 \(0\) 或 \(1\)，第二个 int 维护如果确定是 0 或 1 了那么具体是 0 还是 1。

例如，对于单个字符串，它所有的为 ? 的位置，在第一个 int 中对应位置是 0，所有为 0 或 1 的位置，在第在个 int 中对应的位置是 1，在第二个 int 中对应的位置是自身的值。

考虑 \(a_1,~a_2\) 是询问的左端点到某个字符串之前所维护的两个 int，\(b_1,~b_2\) 是该字符串的两个 int，现在合并这两个信息。

如果某一位置即不可以是 \(1\)，也不可以是 \(0\)，那么该字符串不为 ? 的位置在 \(b_2\) 中对应的值应该至少有一个和 \(a_2\) 中对应位置的值且 \(a_1\) 的该位置为 \(1\)，位运算可以表现为 \((a1~\&~b_1)~\&~(a_2~\oplus~b_2) ~\neq 0\)，则该询问的答案为 \(0\)。

否则这两段信息可以合并：将他们已经确定字符的位置合并起来，然后将确定位置对应的值合并起来即可。于是 \(a_1\) 对 \(b_1\) 取或， \(a_2\) 对 \(b_2\) 取或即可。

最终该询问 \(0/1\) 都可以的位置的个数即为 \(a_1\) 中 \(1\) 的个数。

时间复杂度 \(O(mq)\)，期望得分 \(15~pts\)

子任务 \(5\)：

由于 \(n\) 只有 \(1\)，问题变成了求某个区间内的字符是不是全是 0，全是 1，全是 ? 或 0 和 1 都有。可以考虑用线段树非常轻松的维护这样的信息。

时间复杂度 \(O(q \log m)\)，期望得分 \(15~pts\)

子任务 \(6\)：

世界上没有什么事情是开一棵线段树不能解决的，如果有，那就开 \(30\) 棵。

时间复杂度 \(O(nq \log m)\)，期望得分 \(10~pts\)

子任务 \(7\)：

考虑结合子任务 \(4\) 和子任务 \(5\) 的做法，发现两个区间的状压信息也可以用子任务 \(4\) 的方法合并。因此用线段树维护这两个 int 的状压信息即可。

时间复杂度 \(O(q \log m)\)，期望得分 \(30~pts\)