boosting与随机森林

　　   本文原创，转载请注明出处 http://www.cnblogs.com/gufeiyang

　　

本文主要分两部分，boosting 与 随机森林。

　　　 “三个臭皮匠顶一个诸葛亮”是说三个不聪明的人集合在一起往往能战胜一个聪明的人。 在分类上， 如果给定了若干个弱分类器，是否能够集成为一个强分类器。答案是肯定的，boosting就是这么一个思想。

boosting里边最有名的算法是adaboost。 adaboost是迭代产生集成分类器的算法。 通过每次增大分类错误case的权重，减小分类正确的权重，来达到准确分类的目的。

具体流程如下：

　　　              

这是整个boosting的过程。 但是细心的话会发现上述的算法只能解决二元分类的问题，对于多元分类最终的预测函数为：

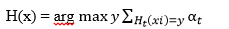
随机森林：既然是森林，那么就要有很多的树， 比如数目为T。 随机森林的每棵树都是一个决策树。 对于给的数据集M，数据集有n条记录，有放回地抽样n次，用抽样的数据集建立一棵决策树。这样重复T次就建立了T个决策树。 需要注意的是：每棵树选择不同的featurns作为树的分裂属性。 这样子就会有T个弱分类的决策树形成了。 这棵树可以通过投票的方式对新的数据进行分类。

随机森林与boosting的集合， 在利用boosting算法的时候，分类器H(X)选择决策树（随机森林的方法建立），这样就形成了有boosting思想的决策树。 boosting是一个将若干弱分类组合形成强分类器的算法， 有着很好的泛化能力。