AVL排序二叉树树

AVL树第一部分，（插入）

---

AVL树是一种自平衡二叉搜索树(BST)，其中对于所有节点，左右子树的高度差不能超过1。

一个AVL树的示例

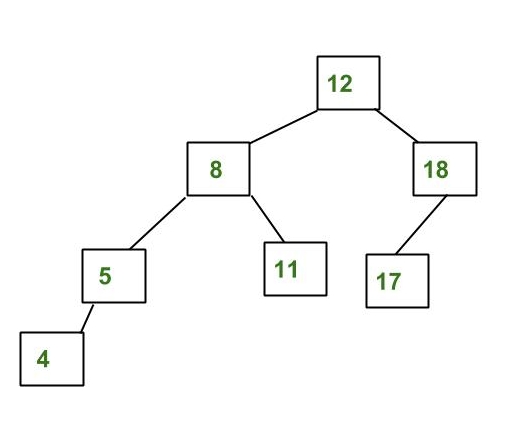
上面的树是AVL树，因为每个节点的左子树和右子树的高度之间的差小于或等于1。

一个非AVL树的示例



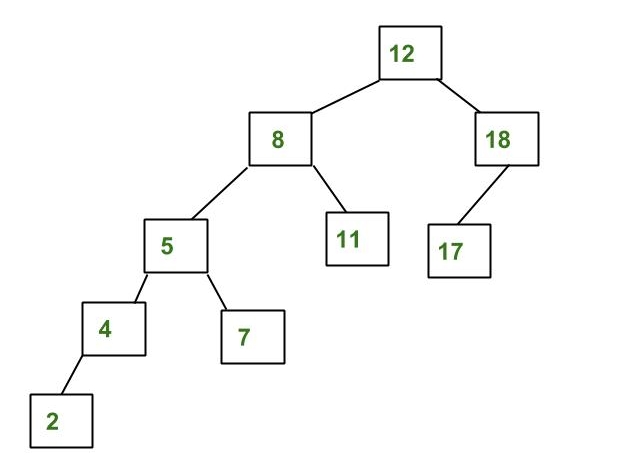
上面的树不是AVL树，因为 8 和 18 的左子树和右子树之间的高度差大于 1。

为什么要用AVL树？

大多数二叉查找树(BST)操作(例如，搜索，找最大，找最小，插入，删除等)所用时间为 \(O(H)\)，其中H是BST的高度。较糟糕的情况是，对于倾斜的二叉树，这些操作的成本可以变为 \(O(N)\)。但是如果我们确保在每次插入和删除后树的高度保持 \(O(logN)\)，那么我们可以保证所有这些操作的上限为 \(O(logN)\)。

插入操作

为了确保给定的树在每次插入后都保持AVL，我们必须增加标准的BST插入操作来执行一些重新平衡。下面是可以执行的两个基本操作，可以在不违反BST属性 (即 keys(left) < key(root) < keys(right)) 的情况下重新平衡BST。

1. 左旋操作 Left Rotation
2. 右旋操作 Right Rotation

T1、T2和T3是以y(左侧)或x(右侧)为根的树的子树
     y                               x
    / \     Right Rotation          /  \
   x   T3   - - - - - - - >        T1   y
  / \       < - - - - - - -            / \
 T1  T2     Left Rotation            T2  T3
上述两个树中的键遵循以下顺序（即二叉查找树的属性）
 keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)
因此BST属性在任何地方都不会被打乱。

插入要遵循的步骤

• 设新插入的节点为 w
• 执行w的标准BST插入
• 从w开始，向上行进，找到第一个不平衡节点。设z是第一个不平衡节点，y是从w到z的路径上的z的子节点，x是从w到z的路径上的z的孙子节点。
• 通过对以z为根的子树执行适当的旋转来重新平衡树。可以有4种可能的情况需要处理，因为x，y和z可以按4种方式排列。以下是可能的4种安排：
  • y是z的左子，x是y的左子(左左大小写)
  • y是z的左子项，x是y的右子项(左右大小写)
  • y是z的右孩子，x是y的右孩子(右大小写)
  • y是z的右子，x是y的左子(右左大小写)

以下是在上述4种情况下要进行的操作。在所有情况下，我们只需要重新平衡以z为根的子树，当以z为根的子树的高度(经过适当的旋转)变得与插入前相同时，完整的树就会变得平衡。

• Left Left Case

    T1, T2, T3 and T4 are subtrees.
         z                                      y
        / \                                   /   \
       y   T4      Right Rotate (z)          x      z
      / \          - - - - - - - - ->      /  \    /  \
     x   T3                               T1  T2  T3  T4
    / \
  T1   T2
  

• Left Right Case

         z                               z                           x
        / \                            /   \                        /  \
       y   T4  Left Rotate (y)        x    T4  Right Rotate(z)    y      z
      / \      - - - - - - - - ->    /  \      - - - - - - - ->  / \    / \
    T1   x                          y    T3                    T1  T2 T3   T4
        / \                        / \
      T2   T3                    T1   T2
  
  

• Right Right Case

    z                                y
   /  \                            /   \
  T1   y     Left Rotate(z)       z      x
      /  \   - - - - - - - ->    / \    / \
     T2   x                     T1  T2 T3  T4
         / \
        T3  T4
  
  

• Right Left Case

     z                            z                            x
    / \                          / \                          /  \
   T1   y   Right Rotate (y)    T1   x      Left Rotate(z)   z      y
       / \  - - - - - - - - ->     /  \   - - - - - - - ->  / \    / \
      x   T4                      T2   y                  T1  T2  T3  T4
     / \                              /  \
   T2   T3                           T3   T4
  
  

图片示例

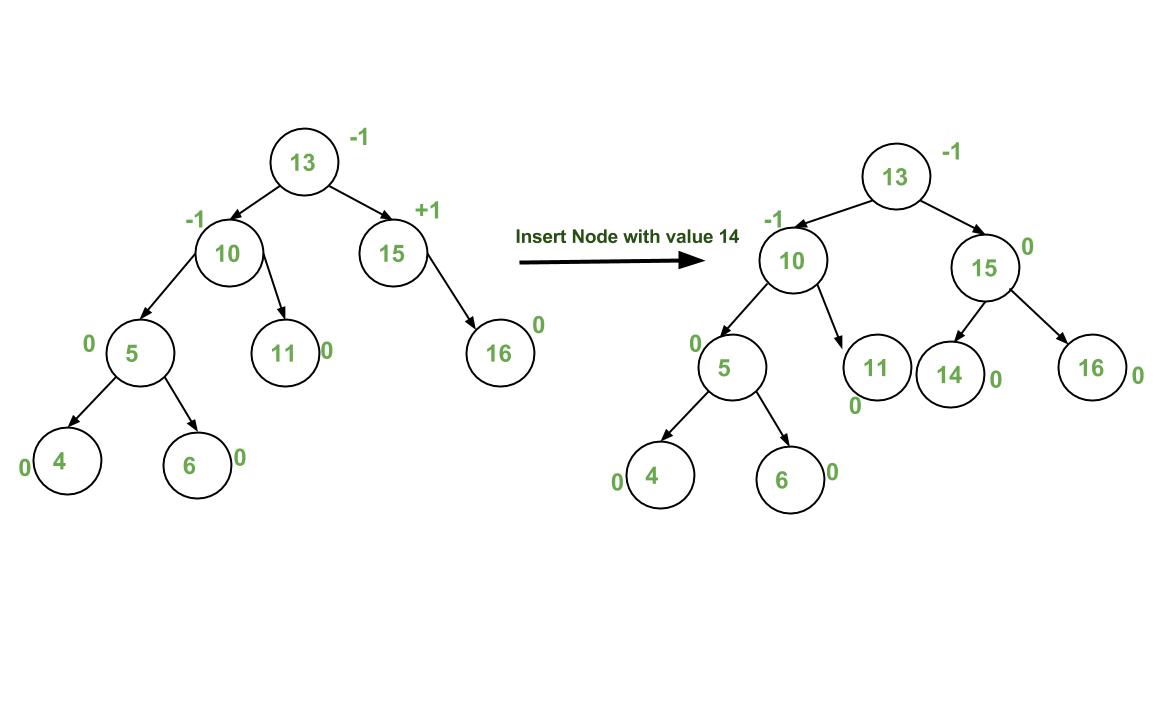
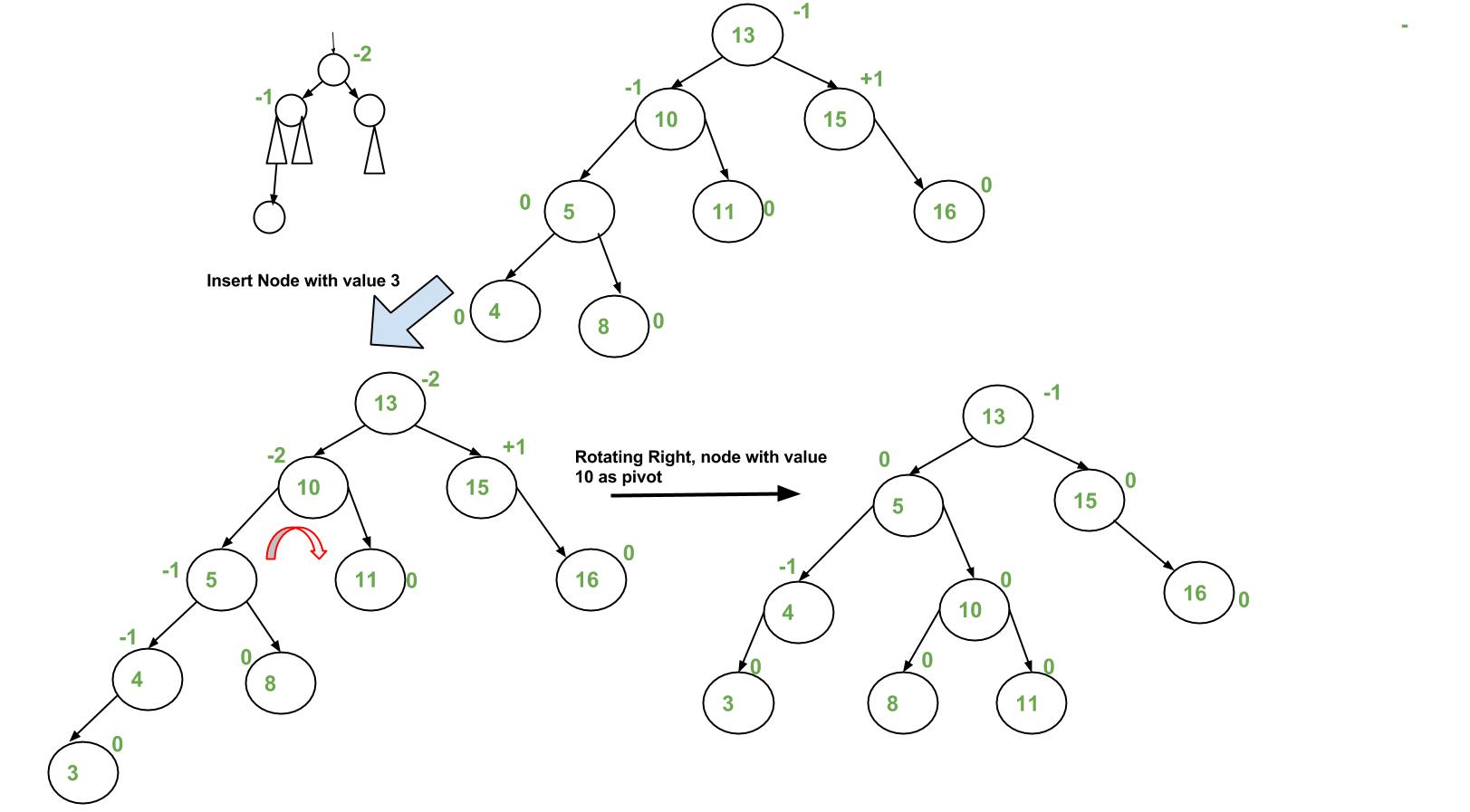
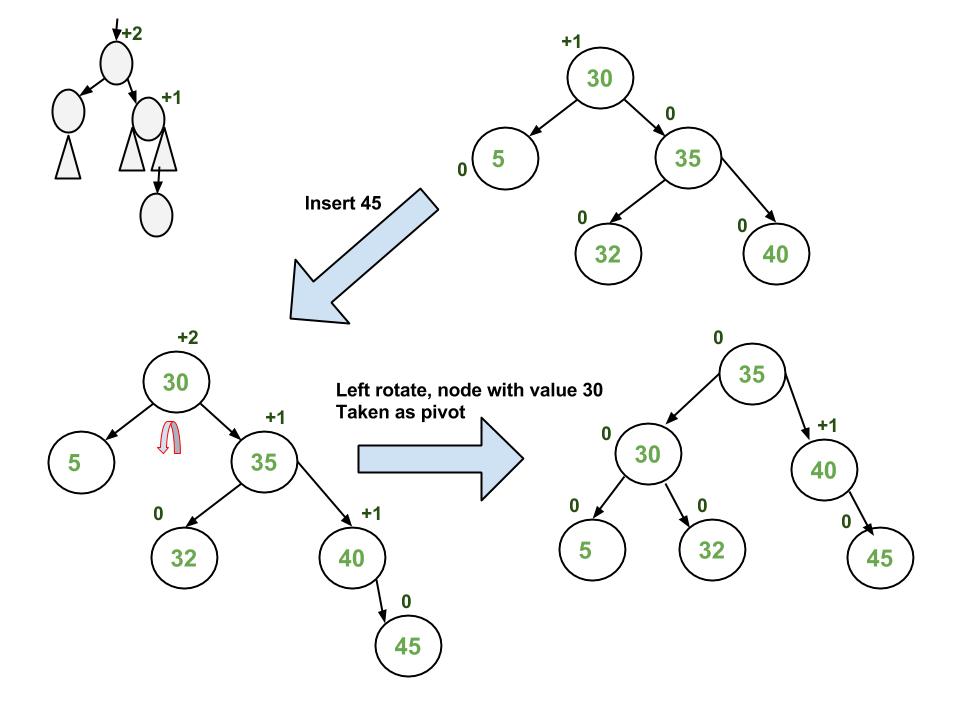
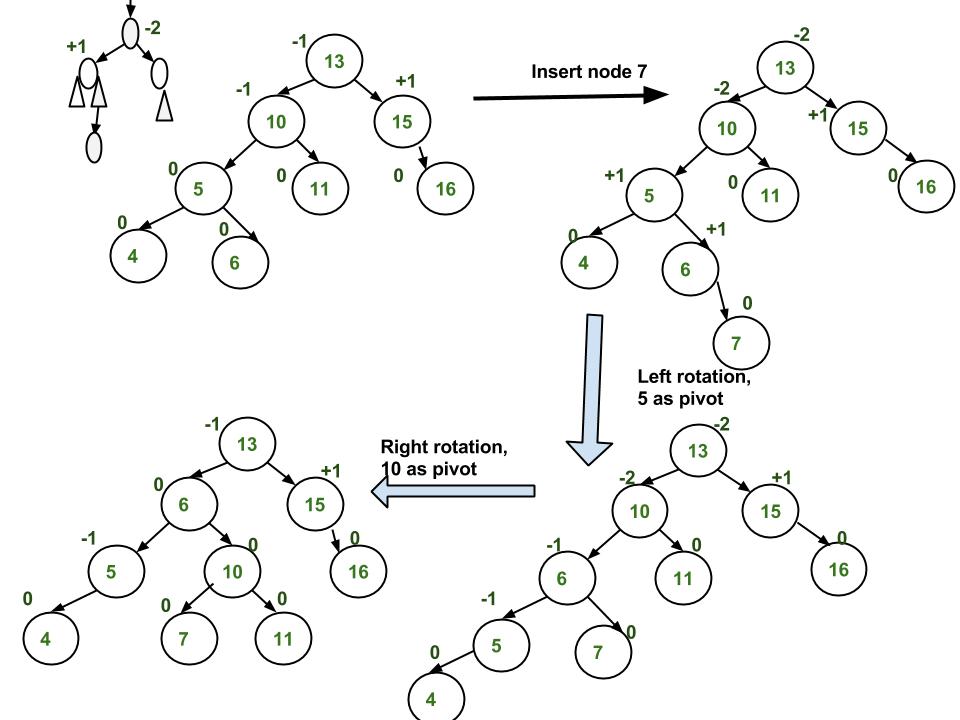
实现

下面是AVL树插入的实现。下面的实现使用递归BST INSERT插入新节点。在递归BST插入中，在插入之后，我们以自底向上的方式一个接一个地获得指向所有祖先的指针。所以我们不需要父指针向上移动。递归代码本身向上行进并访问新插入的节点的所有祖先。

1. 执行正常的BST插入。
2. 当前节点必须是新插入节点的祖先之一。更新当前节点的高度。
3. 获取当前节点的平衡因子(左子树高度-右子树高度)。
4. 如果平衡因子大于1，则当前节点不平衡，我们要么在左左情况下，要么在左右情况下。要检查是否左大小写，请将新插入的key与左子树根中的key进行比较。
5. 如果平衡因子小于-1，则当前节点不平衡，我们要么是右大小写，要么是左右大小写。要检查是否正确大小写，请将新插入的键与右子树根中的键进行比较。

#include <stdio.h>
#include <stdlib.h>

typedef struct avlTreeNode {
    int key;
    struct avlTreeNode *left;
    struct avlTreeNode *right;
    int height;
} avlTreeNode;

// 新建一个二叉树节点
avlTreeNode *newNode(int key)
{
    avlTreeNode *node = malloc(sizeof(avlTreeNode));

    node->height = 1;
    node->key = key;
    node->left = NULL;
    node->right = NULL;

    return node;
}

// 辅助函数，返回最大值
int max(int a, int b)
{
    return (a > b) ? a : b;
} 

// 获取二叉树的高度
int height(avlTreeNode *node)
{
    if (node == NULL)
        return 0;
    return node->height;
} 

// 获取节点 node 的平衡因子, 即 node 下的左右子树的高度差
int getBalance(avlTreeNode *node)
{
    if(node == NULL)
        return 0;
    return height(node->left) - height(node->right);
}

/*
                y                               x
               / \     Right Rotation          /  \
              x   T3   – - – - – - – >        T1   y
             / \       < - - - - - - -            / \
            T1  T2     Left Rotation            T2  T3
*/

// 向右旋转以 y 为根的树
avlTreeNode *rightRotate(avlTreeNode *y)
{
    avlTreeNode *x = y->left;
    avlTreeNode *T2 = x->right;

    // 进行旋转
    x->right = y;
    y->left = T2; 

    // 更新高度
    y->height = max(height(y->left), height(y->right)) + 1;
    x->height = max(height(x->left), height(x->right)) + 1;

    return x;
}

/*
                y                               x
               / \     Right Rotation          /  \
              x   T3   – - – - – - – >        T1   y
             / \       < - - - - - - -            / \
            T1  T2     Left Rotation            T2  T3
*/

// 向右旋转以 y 为根的树
avlTreeNode *leftRotate(avlTreeNode *x)
{
    avlTreeNode *y = x->right;
    avlTreeNode *T2 = y->left;

    // 进行旋转
    y->left = x;
    x->right = T2; 

    // 更新高度
    x->height = max(height(x->left), height(x->right)) + 1;
    y->height = max(height(y->left), height(y->right)) + 1;

    return y;
}

// 给定非空的二叉搜索树，
// 返回在该树中找到的具有最小键值的节点。
// 请注意，不需要搜索整个树
avlTreeNode * minValueNode(avlTreeNode* node)
{
    avlTreeNode *currrnt = node;

    while(currrnt->left != NULL)
        currrnt = currrnt->left;
    return currrnt;
}

// 向AVL二叉树插入一个节点
avlTreeNode *avlTreeInsert(avlTreeNode *root, int key)
{
    // 1、执行正常的BST插入操作
    if(root == NULL)
        return newNode(key);
    // 如果键值已经存在
    if(key == root->key)
        return root;
    if(key < root->key)     //小于往左分支插
        root->left = avlTreeInsert(root->left, key);
    else
        root->right = avlTreeInsert(root->right, key);

    // 2、更新BST的高度, 即左右节点高度的最大值 + 1
    root->height = max(height(root->left), height(root->right)) + 1;

    // 3、获取该根节点的平衡因子，检查该节点是否变得不平衡
    int balance = getBalance(root); 

    // 如果此节点变得不平衡，则有4种情况, 这是由于插入导致的

    // 左 左 过长的原因
    if(balance > 1 && key < root->left->key)
        return rightRotate(root);  

    // 右 右 过长原因
    if(balance < -1 && key > root->right->key)
        return leftRotate(root);

    // 左 右 过长
        // Left Right Case
    if(balance > 1 && key > root->left->key) {
        root->left = leftRotate(root->left);
        return rightRotate(root);
    }  

    // 右 左 过长
    if(balance < -1 && key < root->right->key) {
        root->right = rightRotate(root->right);
        return leftRotate(root);
    }  

    // 若没做任何改变，返回原值
    return root;
}

avlTreeNode *avlTreeDelete(avlTreeNode *root, int key)
{
    // 1、基本查找二叉树的删除
    if(root == NULL)
        return root;
    // 小于当前节点，则向左边查找删除
    if(key < root->key)
        root->left = avlTreeDelete(root->left, key);
    // 大于当前节点，则向右边查找删除
    else if (key > root->key) {
        root->right = avlTreeDelete(root->right, key);
    // 如果要删除的是当前 root 节点
    } else {
        // 当前根节点只有一个字节点或者没有子节点
        if(root->left == NULL || root->right == NULL) {
            avlTreeNode *temp = root->left ?
                root->left : root->right;

            // 没有子节点情况, 直接删除该节点
            if(temp == NULL) {
                temp = root;
                root = NULL;
            // 有一个子节点情况，将字节点复制给根
            } else {
                *root = *temp;
            }
            free(temp);
        // 当前根节点包含两个子节点
        } else {
            // 获取右子树的后续节点中的最小值
            // 因为删除根节点后，右子树的最小值刚好适合做根节点的值
            avlTreeNode *temp =  minValueNode(root->right);

            // 复制该后续节点值给当前要删除的根节点
            root->key = temp->key;

            // 删除该后续最小值节点
            root->right = avlTreeDelete(root->right, temp->key);
        }
    }

    // 删除完后，如果树为空
    if(root == NULL)
        return root;

    // 2、更新当前节点的高度
    root->height = max(height(root->left), height(root->right)) + 1;

    // 3、获取平衡因子
    int balance = getBalance(root);

    // 如果此节点变得不平衡，则有4种情况, 这是由于删除导致的

	// Left Left Case
	if (balance > 1 && getBalance(root->left) >= 0)
		return rightRotate(root); 

	// Left Right Case
	if (balance > 1 && getBalance(root->left) < 0) {
		root->left = leftRotate(root->left);
		return rightRotate(root);
	} 

	// Right Right Case
	if (balance < -1 && getBalance(root->right) <= 0)
		return leftRotate(root); 

	// Right Left Case
	if (balance < -1 && getBalance(root->right) > 0) {
		root->right = rightRotate(root->right);
		return leftRotate(root);
	}

    return root;
}

void preOrder(avlTreeNode *root)
{
    if(root != NULL)
    {
        preOrder(root->left);
        printf("%d ",root->key);
        preOrder(root->right);
    }
}  

int main()
{
    avlTreeNode *root = NULL;
    root = avlTreeInsert(root, 9);
    root = avlTreeInsert(root, 5);
    root = avlTreeInsert(root, 10);
    root = avlTreeInsert(root, 0);
    root = avlTreeInsert(root, 6);
    root = avlTreeInsert(root, 11);
    root = avlTreeInsert(root, -1);
    root = avlTreeInsert(root, 1);
    root = avlTreeInsert(root, 3);
    root = avlTreeInsert(root, 4);

    root = avlTreeDelete(root, 10); 

    preOrder(root);
    printf("\n");
}