VIJOS-P1320 清点人数

JDOJ 1427: VIJOS-P1320 清点人数

题目传送门

Description

初始时，火车上没有学生；当同学们开始上火车时，年级主任从第一节车厢出发走到最后一节车厢，每节车厢随时都有可能有同学上下。年级主任走到第m节车厢时，他想知道第１到m这m节车厢上一共有多少学生，但是他没有调头往回走的习惯．也就是说每次当他提问时，m总会比前一次大。

Input

第一行两个整数n,k，表示火车共有n节车厢以及k个事件。接下来有k行，按时间先后给出k个事件，每行开头都有一个字母A,B或C，如果字母为A，接下来是一个数m，表示年级主任现在在第m节车厢；如果为B，接下来两个数m,p，表示在第m节车厢有p名学生上车；如果为C，接下来两个数m,p，表示在第m节车厢有p名学生下车。学生总人数不会超过100000。

Output

有多少个A就输出多少行，每行一个整数，回答年级主任提出的问题。

Sample Input

10 7 A 1 B 1 1 B 3 1 B 4 1 A 2 A 3 A 10

Sample Output

0 1 2 3

HINT

注意:对于30%的数据,n< =10000,k< =10000 至少有3000个A 对于100%的数据n< =500000,k< =100000. 至少有30000个A

题解：

树状数组模板题。

因为这是本蒟蒻A掉的第一道树状数组的题目，所以在这里索性介绍一下树状数组。

树状数组其实是一种数据结构，它的作用就是优化查询和修改的操作。试想，我们假如在做一道题的时候使用裸的一维数组来存储数据，那每次区间修改需要O(1)的时间，但查询却需要O(n)的时间，针对于某些题目“比如本题”，必然会TLE。所以我们使用树状数组来优化这两个操作，使得修改和查询均可以在O(logn)的时间内完成，提升效率。

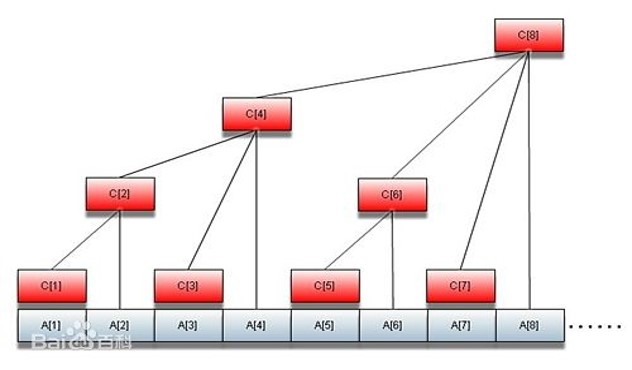
（这是百度百科上树状数组的图）

可以直观地看出树状数组是个什么模式，是的，这就是一棵树，而这棵树上每个节点存储的数据就是它所有儿子节点的数据和。所以我们就可以在树上做修改和区间查询（节点减节点），来做到树状数组的优化。

树状数组的实现需要三个特别重要的函数，我一般把它们写成fix()（向上修改），getsum()（向下查询），和lowbit()（这个函数是理解树状数组运行过程的关键）。

首先从最关键的lowbit函数入手。

它长这个样子：

int lowbit(int x)
{
    return x+=x&-x;
}

这里还涉及到了位运算的相关知识，这里我不想加以叙述，对其感兴趣的小伙伴可以上网查找相关知识。那么这个lowbit函数是干什么用的呢？

我们可以把它理解成对树状数组的遍历方式。

根据树状数组的示意图可以发现，我们如果想对原数组进行元素修改，会牵连到于之关联的树状数组整个链。所以我们必须层层向上修改，每一层都要修改，才能保证树状数组存储的元素的正确性。

那么这个层层向上（向下），就需要lowbit这个函数，或者是说这个功能，来实现。

下面介绍fix()（修改函数）

void fix(int x)
{
    for(int i=x;i<=n;i+=i&-i)
        c[i]++;
}
void fix(int x,int y)//表示在x元素处修改y个单位
{
    for(int i=x;i<=n;i+=i&i)
        c[i]+=y;
}

通过刚才学习lowbit函数，我们应该可以理解这个循环的含义。

其实就是层层向上修改树状数组的对应元素。

然后是getsum()（查询函数），实现内容大同小异。

int getsum(int x)
{
    int ret=0;
    for(int i=x;i;i-=i&-i)
        ret+=c[i];
    return ret;
}

这里注意，查询的时候要从上往下查询，这里默认查询的区间是1-->x，如果不是1到x，需要另外加参数。

所以树状数组知识介绍完之后，我们就可以轻松地A这道题。

代码如下：

#include<cstdio>
using namespace std;
int n,k,c[500001];
char s[4];
void fix(int x,int y)
{
	for(int i=x;i<=n;i+=i&-i)
		c[i]+=y;
}
void getsum(int x)
{
	int ret=0;
	for(int i=x;i;i-=i&-i)
		ret+=c[i];
	printf("%d\n",ret);
}
int main()
{
	scanf("%d%d",&n,&k);
	for(int i=1;i<=k;i++)
	{
		scanf("%s",s);
		if(s[0]=='A')
		{
			int x;
			scanf("%d",&x);
			getsum(x);
		}
		else if(s[0]=='B')
		{
			int x,y;
			scanf("%d%d",&x,&y);
			fix(x,y);
		}
		else if(s[0]=='C')
		{
			int x,y;
			scanf("%d%d",&x,&y);
			fix(x,-y);
		}
	}
	return 0;
}