HDU-4190-Number Sequence-容斥原理+多重集和的r组合

HDU-4190-Number Sequence-容斥原理+多重集和的r组合

---

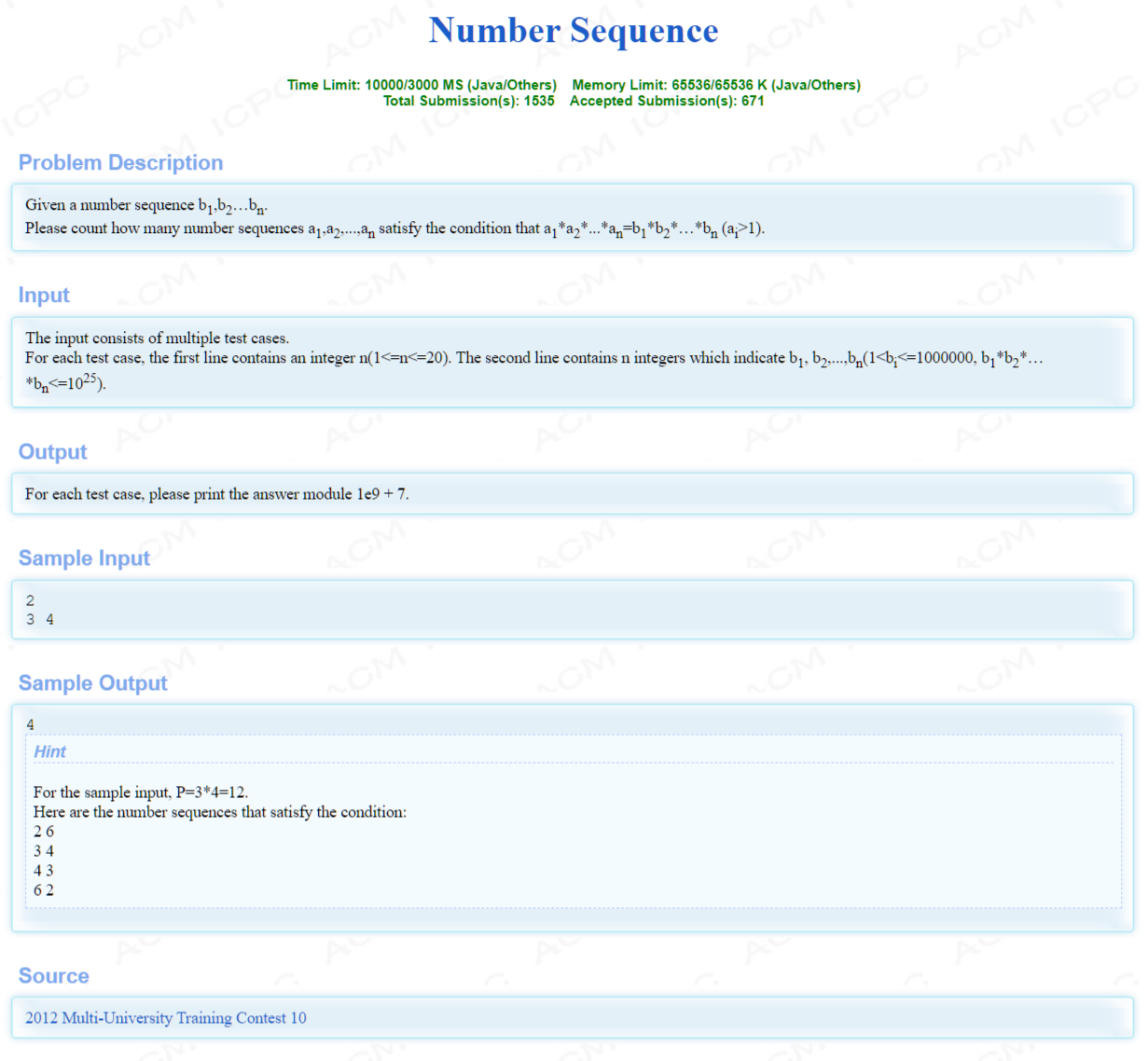
【Problem Description】

给你\(n\)个数\(b_i\)，问有多少个长度为\(n\)序列\(a_i\)，使得\(a_1\cdot a_2\dots a_n=b_1\cdot b_2\dots b_n\)。且\(a_i>1\)。

【Solution】

将所有\(b_i\)分解质因数，并分别统计每个质因数出现的次数，那么可以肯定，所有的\(a_i\)一定是从这些质因数中选取不同的组合相乘得到的。

假设没有\(a_i>1\)的限制，然后假设所有的\(b_i\)共有\(3\)个质因子，每个质因子出现的次数分别为\(a,b,c\)次。则总共有\({a+n-1\choose n-1}\cdot {b+n-1\choose n-1}\cdot {c+n-1\choose n-1}\)种长度为\(n\)的\(a_i\)序列。即类似总共有\(n\)个不同的盒子，将\(a\)个红球，\(b\)个蓝球，\(c\)个绿球放进这\(n\)个盒子中有多少种不同的方案，可以使得。

但是现在求得的答案数包括了\(a_i=1\)的情况，需要去除，即减去\(1\)个位置为空的方案数，再加上\(2\)个位置为空的方案数，再减去\(\dots\)等等。\(i\)个位置为空的方案数为\({n\choose i}\cdot {a+n-1-i\choose n-1-i}\cdot {b+n-1-i\choose n-1-i}\cdot {c+n-1-i\choose n-1-i}\)。即先从\(n\)个盒子种选\(i\)个位置，有\({n\choose i}\)种方案，然后再乘以将\(a\)个红球，\(b\)个蓝球，\(c\)个绿球放进\(n-i\)个盒子中的方案数。

---

【Code】

#include<iostream>
#include<algorithm>
#include<map>
#include<cstring>
#include<cstdio>
using namespace std;
#define INF 0x3f3f3f3f
#define maxn 1000005
#define int long long
const int mod=1e9+7;
int a[25];
int prime[maxn],cnt=0;
bool vis[maxn]={1,1};
void Euler(){ //欧拉筛
	for(int i=2;i<maxn;i++){
		if(!vis[i]) prime[++cnt]=i;
		for(int j=1;j<=cnt&&i*prime[j]<maxn;j++){
			vis[i*prime[j]]=1;
			if(i%prime[j]==0) break;
		}
	}
}
map<int,int>mp; //统计每个质因数出现的次数
void solve(int n){ //求质因数
	for(int i=1;i<=cnt&&prime[i]*prime[i]<=n;i++){
		int p=prime[i],num=0;
		if(n%p==0){
			while(n%p==0) n/=p,num++;
			mp[p]+=num;
		}
	}
	if(n>1) mp[n]++;
}
int C[105][105]; //组合数
signed main(){
	ios::sync_with_stdio(false);
	cin.tie(0);Euler();
	for(int i=0;i<105;i++) C[i][0]=1;
	for(int i=1;i<105;i++){ //预处理组合数
		for(int j=1;j<=i;j++){
			C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
		}
	}
	int n;
	while(cin>>n){
		mp.clear();
		for(int i=1;i<=n;i++) cin>>a[i],solve(a[i]);
		int ans=1;
		for(auto v:mp){ //求出ai没有限制时的方案数
			ans=(ans*C[v.second+n-1][n-1])%mod;
		}
		for(int i=1;i<n;i++){ //容斥减去ai=1的方案
			int tmp=C[n][i];
			for(auto v:mp){
				tmp=tmp*C[v.second+n-1-i][n-1-i]%mod;
			}
			ans=(ans+(i&1?-1:1)*tmp)%mod;
		}
		cout<<(ans+mod)%mod<<endl;
	}
	return 0;
}