博弈论经典算法（一）——对抗搜索与Alpha-Beta剪枝

前言

在一些复杂的博弈论题目中，每一轮操作都可能有许多决策，于是就会形成一棵庞大的博弈树。

而有一些博弈论题没有什么规律，针对这样的问题，我们就需要用一些十分玄学的算法。

例如对抗搜索。

对抗搜索简介

一、对抗搜索的适用范围

在博弈论题目中，如果决策双方的获胜条件是截然相反的，即一方要求得分越高越好，另一方要求得分越低越好，这时我们就可以用上对抗搜索算法。

二、对抗搜索的主要思想

对抗搜索的核心思想就是$dfs$遍历一遍博弈树。

不难想到，如果博弈树非常庞大，在不加优化的情况下，对抗搜索的时间效率是十分低下的。

因此，我们就需要对对抗搜索进行一定的优化。

三、对抗搜索的优化

对抗搜索的优化一般来讲有两种：记忆化和 $Alpha-Beta$剪枝 。

不过需要注意，如果两个优化一起使用，很可能会产生化学反应出现一些奇妙的$Bug$（我已经亲身体验过了）。

对抗搜索优化一：记忆化

记忆化应该是搜索中一个比较常用的技巧。

一、大致思路

它的大致思路就是，对于当前的某一种状态，在求解后将结果记录下来，下一次再访问到时直接将存下来的结果返回即可。

二、模板

记忆化优化对抗搜索的伪代码如下：

inline int dfs(Status s,int Which)//Status记录当前状态，Which记录当前操作的选手，其中0号选手取Max，1号选手取Min

{

    if(res[s]) return res[s];//如果之前已经求出过这个状态的结果，直接返回

    if(IsEnd(s)) return GetVal(s);//如果当前状态已经为最终状态，就返回当前状态的分值

    register int i,ans=Which?1e9:0;

    extend(s);//扩展当前状态，并将新状态存储于NewStatus数组中，用NewStatusTotal记录新状态的数量

    for(i=1;i<=NewStatusTotal;++i)//枚举从当前状态能够扩展到的新状态

   		ans=Which?min(ans,dfs(NewStatus[i],Which^1):max(ans,dfs(NewStatus[i],Which^1);//不断dfs，更新ans

    return res[s]=ans;//将最终求解出的结果存储下来

}

对抗搜索优化二：$Alpha-Beta$剪枝

$Alpha-Beta$剪枝应该是对抗搜索一个比较巧妙的优化。

一、大致思路

如图是一棵博弈树：

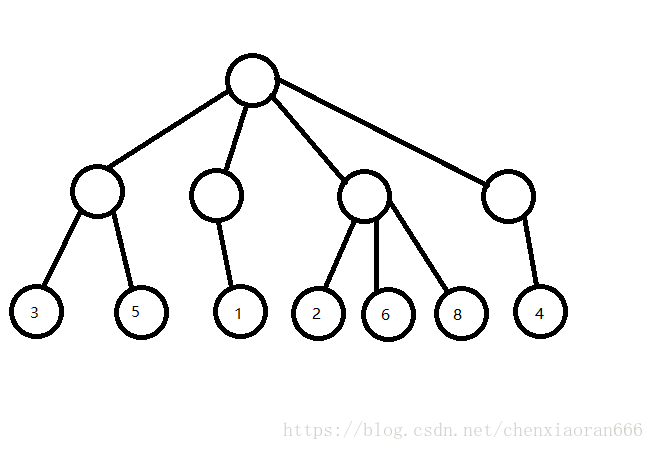
假设第一个决策者的目的是取最大值，第二个决策者的目的是取最小值。

在搜索完根节点的两个子节点后，博弈树就会变成这样：

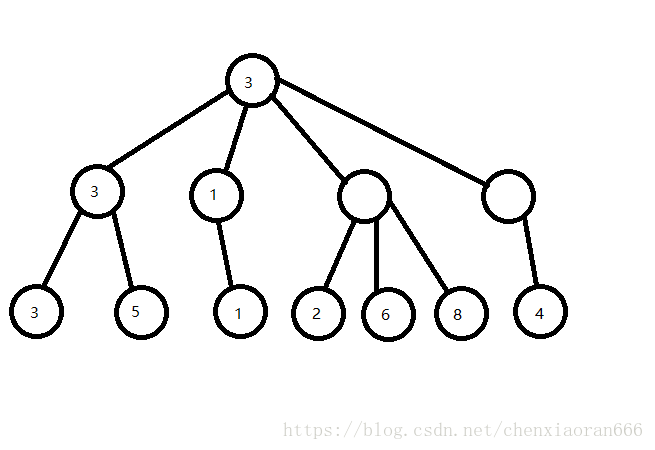
这时，我们再来看根节点的第三个子节点。

不难发现，在处理完第三个节点的第一个子节点之后，第三个节点的权值就会变成$2$。

因为第三个节点的目标是取最小值，因此最终第三个节点的权值必定小于等于$2$。

而根节点的目标是取最大值，且此时根节点的权值已经为$3$了。

也就是说，第三个节点对最终答案肯定是没有任何贡献的。

因此对于第三个节点的剩余两个状态，我们就无需继续搜索了，可以直接退出。

这就是传说中的$Alpha-Beta$剪枝了。

二、模板

$Alpha-Beta$剪枝优化对抗搜索的伪代码如下：

inline int dfs(Status s,int Alpha,int Beta,int Which)//Status记录当前状态，Which记录当前操作的选手，其中0号选手取Max，1号选手取Min

//Alpha存储较大值，Beta存储较小值

//如果当前节点是取Max的节点，则Alpha表示当前节点父亲的父亲的权值，Beta表示当前节点父亲的权值

//如果当前节点是取Min的节点，则Alpha表示当前节点父亲的权值，Beta表示当前节点父亲的父亲的权值

{

    if(IsEnd(s)) return GetVal(s);//如果当前状态已经为最终状态，就返回当前状态的分值

    register int i;

    extend(s);//扩展当前状态，并将新状态存储于NewStatus数组中，用NewStatusTotal记录新状态的数量

    for(i=1;i<=NewStatusTotal;++i)//枚举从当前状态能够扩展到的新状态

    {

        t=dfs(NewStatus,Alpha,Beta,Which^1);//求出当前枚举到的新状态的分值

        (s.Which?Beta=min(Beta,t):Alpha=max(Alpha,t)); //如果当前节点取min，就更新Beta，否则更新Alpha

        if(Alpha>=Beta) break;//如果Alpha≥Beta，就说明这个节点对最终答案没有贡献了，就结束搜索

    }

    return s.Which?Beta:Alpha;//返回相应值

}

后记

对抗搜索的核心内容差不多也就是这些。

但是，如果真正用起来，对抗搜索其实还是挺复杂的。

下面推荐一道例题：【BZOJ3106】[CQOI2013] 棋盘游戏