洛谷 P1801 黑匣子_NOI导刊2010提高（06）

题目描述

Black Box是一种原始的数据库。它可以储存一个整数数组，还有一个特别的变量i。最开始的时候Black Box是空的．而i等于0。这个Black Box要处理一串命令。

命令只有两种：

ADD(x):把x元素放进BlackBox;

GET:i加1，然后输出Blackhox中第i小的数。

记住：第i小的数，就是Black Box里的数的按从小到大的顺序排序后的第i个元素。例如：

我们来演示一下一个有11个命令的命令串。（如下图所示）

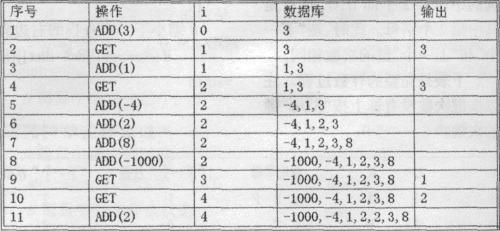
现在要求找出对于给定的命令串的最好的处理方法。ADD和GET命令分别最多200000个。现在用两个整数数组来表示命令串：

1.A(1)，A(2)，…A(M)：一串将要被放进Black Box的元素。每个数都是绝对值不超过2000000000的整数，M$200000。例如上面的例子就是A=(3，1，一4，2，8，-1000，2)。

2.u(1)，u(2)，…u(N)：表示第u(j)个元素被放进了Black Box里后就出现一个GET命令。例如上面的例子中u=(l，2，6，6)。输入数据不用判错。

输入输出格式

输入格式：

第一行，两个整数，M，N。

第二行，M个整数，表示A(l)

……A(M)。

第三行，N个整数，表示u(l)

…u(N)。

输出格式：

输出Black Box根据命令串所得出的输出串，一个数字一行。

输入输出样例

输入样例#1：

7 4
3 1 -4 2 8 -1000 2
1 2 6 6

输出样例#1：

3
3
1
2

说明

对于30%的数据，M≤10000;

对于50%的数据，M≤100000：

对于100%的数据，M≤200000。

思路：一道相对来说比较简单的splay题目，因为只涉及到insert(插入)和kth(查询第k大)操作，然后依照题目所说的来插入求第k大即可，都是splay的经典操作。但是这道题还有一个坑点就是我们的inf要设为0x7f，而不能是0x3f3f3f3f，因为数据范围是会爆0x3f3f3f3f的，这个要注意一下，不然只有90分。

代码：

#include<cstdio>
#include<cctype>
#define maxn 200007
using namespace std;
int n,m,root,tot,a[maxn];
inline int qread() {
  char c=getchar();int num=0,f=1;
  for(;!isdigit(c);c=getchar()) if(c=='-') f=-1;
  for(;isdigit(c);c=getchar()) num=num*10+c-'0';
  return num*f;
}
struct Tree {
  int fa,ch[2],siz,val,cnt;
}t[maxn];
inline void pushup(int rt) {
  t[rt].siz=t[t[rt].ch[0]].siz+t[t[rt].ch[1]].siz+t[rt].cnt;
}
inline void rotate(int x) {
  int y=t[x].fa,z=t[y].fa;
  int k=t[y].ch[1]==x;
  t[z].ch[t[z].ch[1]==y]=x;
  t[x].fa=z;
  t[y].ch[k]=t[x].ch[k^1];
  t[t[x].ch[k^1]].fa=y;
  t[x].ch[k^1]=y,t[y].fa=x;
  pushup(y),pushup(x);
}
inline void splay(int x, int rt) {
  while(t[x].fa!=rt) {
    int y=t[x].fa,z=t[y].fa;
    if(z!=rt) (t[y].ch[0]==x)^(t[z].ch[0]==x)?rotate(x):rotate(y);
    rotate(x);
  }
  if(!rt) root=x;
}
inline void insert(int x) {
  int u=root,f=0;
  while(u&&t[u].val!=x) {
    f=u;
    u=t[u].ch[x>t[u].val];
  }
  if(u) t[u].cnt++;
  else {
    u=++tot;
    if(f) t[f].ch[x>t[f].val]=u;
    t[u].fa=f;t[u].val=x;
    t[u].cnt=t[u].siz=1;
  }
  splay(u,0);
}
inline int kth(int x) {
  int u=root;
  if(t[u].siz<x) return 0;
  while(233) {
    int y=t[u].ch[0];
    if(x>t[y].siz+t[u].cnt) {
      x-=t[y].siz+t[u].cnt;
      u=t[u].ch[1];
    }
    else if(t[y].siz>=x) u=y;
    else return t[u].val;
  }
}
int main() {
  m=qread(),n=qread();
  insert(0x7fffffff),insert(-0x7fffffff);
  for(int i=1;i<=m;++i) a[i]=qread();
  int j=1;
  for(int i=1,x;i<=n;++i) {
    x=qread();
    for(;j<=x;++j) insert(a[j]);
    printf("%d\n",kth(i+1));
  }
  return 0;
}