五、regularized线性回归练习（转载）

转载链接：http://www.cnblogs.com/tornadomeet/archive/2013/03/17/2964515.html

前言：

　　本节主要是练习regularization项的使用原则。因为在机器学习的一些模型中，如果模型的参数太多，而训练样本又太少的话，这样训练出来的模型很容易产生过拟合现象。因此在模型的损失函数中，需要对模型的参数进行“惩罚”，这样的话这些参数就不会太大，而越小的参数说明模型越简单，越简单的模型则越不容易产生过拟合现象。本文参考的资料参考网页：http://openclassroom.stanford.edu/MainFolder/DocumentPage.php?course=DeepLearning&doc=exercises/ex5/ex5.html。主要是给定7个训练样本点，需要用这7个点来模拟一个5阶多项式。主要测试的是不同的regularization参数对最终学习到的曲线的影响。

　　实验基础：

　　此时的模型表达式如下所示：

　　

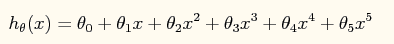
　　模型中包含了规则项的损失函数如下：

　　

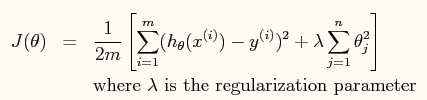
　　模型的normal equation求解为：

　　

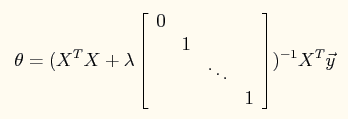
　　程序中主要测试lambda=0,1,10这3个参数对最终结果的影响。

　　一些matlab函数：

　　plot:

　　主要是将plot绘曲线的一些性质。比如说：plot(x,y,'o','MarkerEdgeColor','b','MarkerFaceColor','r')这里是绘制x-y的点图，每个点都是圆圈表示，圆圈的边缘用蓝色表示，圆圈里面填充的是红色。由此可知’MarkerEdgeColor’和’MarkerFaceColor’的含义了。

　　diag:

　　diag使用来产生对角矩阵的，它是用一个列向量来生成对角矩阵的，所以其参数应该是个列向量，比如说如果想产生3*3的对角矩阵，则可以是diag(ones(3,1)).

　　legend：

　　注意转义字符的使用，比如说legned(‘\lambda_0’)，说明标注的是lamda0.

　　实验结果：

　　样本点的分布和最终学习到的曲线如下所示：

　　

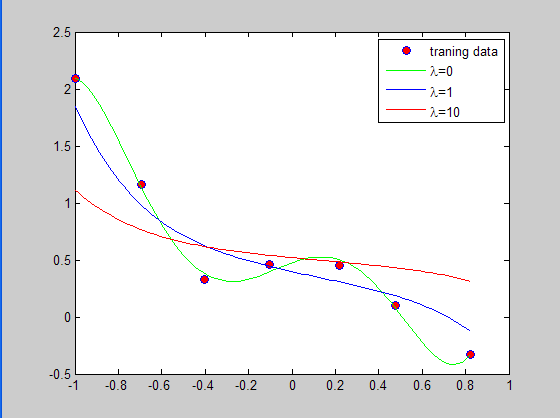
　　可以看出，当lambda=1时，模型最好，不容易产生过拟合现象，且有对原始数据有一定的模拟。

实验主要代码：

clc,clear
%加载数据
x = load('ex5Linx.dat');
y = load('ex5Liny.dat');

%显示原始数据
plot(x,y,'o','MarkerEdgeColor','b','MarkerFaceColor','r')

%将特征值变成训练样本矩阵
x = [ones(length(x),) x x.^ x.^ x.^ x.^];
[m n] = size(x);
n = n -;

%计算参数sidta，并且绘制出拟合曲线
rm = diag([;ones(n,)]);%lamda后面的矩阵
lamda = [  ]';
colortype = {'g','b','r'};
sida = zeros(n+,);
xrange = linspace(min(x(:,)),max(x(:,)))';
hold on;
for i = :
    sida(:,i) = inv(x'*x+lamda(i).*rm)*x'*y;%计算参数sida
    norm_sida = norm(sida)
    yrange = [ones(size(xrange)) xrange xrange.^ xrange.^,...
        xrange.^ xrange.^]*sida(:,i);
    plot(xrange',yrange,char(colortype(i)))
    hold on
end
legend('traning data', '\lambda=0', '\lambda=1','\lambda=10')%注意转义字符的使用方法
hold off