multi-head attention

■ 论文 | Attention Is All You Need

■ 链接 | https://www.paperweekly.site/papers/224

■ 源码 | https://github.com/Kyubyong/transformer

■ 论文 | Weighted Transformer Network for Machine Translation

■ 链接 | https://www.paperweekly.site/papers/2013

■ 源码 | https://github.com/JayParks/transformer

思想：舍弃 RNN，只用注意力模型来进行序列的建模

新型的网络结构： Transformer，里面所包含的注意力机制称之为 self-attention。这套 Transformer 是能够计算 input 和 output 的 representation 而不借助 RNN 的的 model，所以作者说有 attention 就够了。

模型：同样包含 encoder 和 decoder 两个 stage，encoder 和 decoder 都是抛弃 RNN，而是用堆叠起来的 self-attention，和 fully-connected layer 来完成，模型的架构如下：

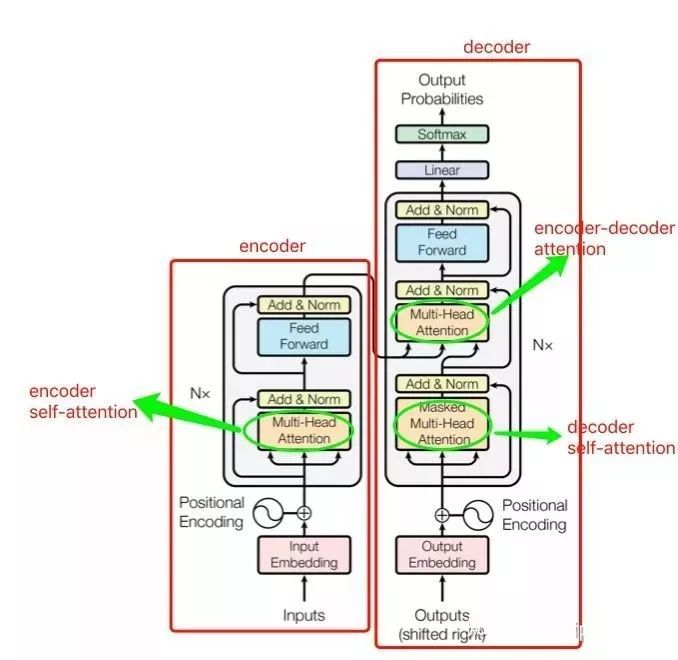
模型共包含三个 attention 成分，分别是 encoder 的 self-attention，decoder 的 self-attention，以及连接 encoder 和 decoder 的 attention。这三个 attention block 都是 multi-head attention 的形式，输入都是 query Q 、key K 、value V 三个元素，只是 Q 、 K 、 V 的取值不同罢了。接下来重点讨论最核心的模块 multi-head attention（多头注意力）。

multi-head attention 由多个 scaled dot-product attention 这样的基础单元经过 stack 而成。

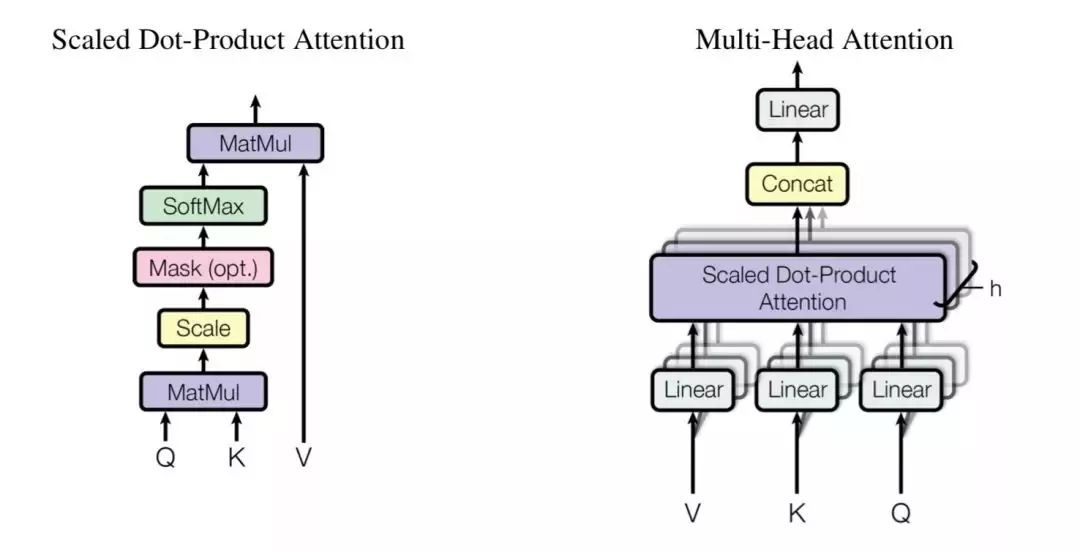
按字面意思理解，scaled dot-product attention 即缩放了的点乘注意力，我们来对它进行研究。

那么 Q、K、V 到底是什么？encoder 里的 attention 叫 self-attention，顾名思义，就是自己和自己做 attention。在传统的 seq2seq 中的 encoder 阶段，我们得到 n 个时刻的 hidden states 之后，可以用每一时刻的 hidden state hi，去分别和任意的 hidden state hj,j=1,2,…,n 计算 attention，这就有点 self-attention 的意思。回到当前的模型，由于抛弃了 RNN，encoder 过程就没了 hidden states，那拿什么做 self-attention 来自嗨呢？

可以想到，假如作为 input 的 sequence 共有 n 个 word，那么我可以先对每一个 word 做 embedding 吧？就得到 n 个 embedding，然后我就可以用 embedding 代替 hidden state 来做 self-attention 了。所以 Q 这个矩阵里面装的就是全部的 word embedding，K、V 也是一样。

所以为什么管 Q 叫query？就是你每次拿一个 word embedding，去“查询”其和任意的 word embedding 的 match 程度（也就是 attention 的大小），你一共要做 n 轮这样的操作。

我们记 word embedding 的 dimension 为 dmodel ，所以 Q 的 shape 就是 n*dmodel， K、V 也是一样，第 i 个 word 的 embedding 为 vi，所以该 word 的 attention 应为：

scaled dot-product attention 基本就是这样了。基于 RNN 的传统 encoder 在每个时刻会有输入和输出，而现在 encoder 由于抛弃了 RNN 序列模型，所以可以一下子把序列的全部内容输进去，来一次 self-attention 的自嗨。

理解了 scaled dot-product attention 之后，multi-head attention 就好理解了，因为就是 scaled dot-product attention 的 stacking。

先把 Q、K、V 做 linear transformation，然后对新生成的 Q’、K’、V’ 算 attention，重复这样的操作 h 次，然后把 h 次的结果做 concat，最后再做一次 linear transformation，就是 multi-head attention 这个小 block 的输出了。

以上介绍了 encoder 的 self-attention。decoder 中的 encoder-decoder attention 道理类似，可以理解为用 decoder 中的每个 vi 对 encoder 中的 vj 做一种交叉 attention。

decoder 中的 self-attention 也一样的道理，只是要注意一点，decoder 中你在用 vi 对 vj 做 attention 时，有一些 pair 是不合法的。原因在于，虽然 encoder 阶段你可以把序列的全部 word 一次全输入进去，但是 decoder 阶段却并不总是可以，想象一下你在做 inference，decoder 的产出还是按从左至右的顺序，所以你的 vi 是没机会和 vj ( j>i ) 做 attention 的。

那怎么将这一点体现在 attention 的计算中呢？文中说只需要令 score(vi,vj)=-∞ 即可。为何？因为这样的话：

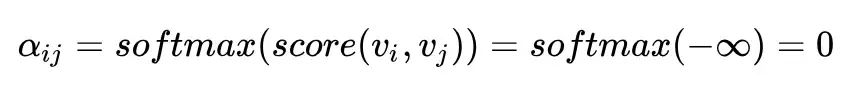
所以在计算 vi 的 self-attention 的时候，就能够把 vj 屏蔽掉。所以这个问题也就解决了。