排序算法<No.5>【堆排序】

算法，是系统软件开发，甚至是搞软件的技术人士的核心竞争力，这一点，我坚信不疑。践行算法实践，已经有一段时间没有practise了，今天来一个相对麻烦点的，堆排序。

1. 什么是堆（Heap）

这里说的堆，是一种数据结构，不是指计算机系统中的存储类型。堆是一种完全二叉树。说到完全二叉树，估计很多人都会想问，什么是完全二叉树，那满二叉树呢？先看看定义完全二叉树和满二叉树：

满二叉树是指这样的一种二叉树：除最后一层外，每一层上的所有结点都有两个子结点。在满二叉树中，每一层上的结点数都达到最大值，即在满二叉树的第k层上有2k-1个结点，且深度为m的满二叉树有2m－1个结点。

完全二叉树是指这样的二叉树：除最后一层外，每一层上的结点数均达到最大值；在最后一层上只缺少右边的若干结点。

一般说的堆数据结构，都是指的二叉堆，二叉堆满足堆特性：父节点的键值总是保持固定的序关系于任何一个子节点的键值，且每个节点的左子树和右子树都是一个二叉堆。

堆的数据，通常是用数组进行存储的。

2. 什么是最大堆和最小堆

二叉堆常见的有最大堆和最小堆，但是不是所有的堆都是最大堆或者最小堆。

当父节点的键值总是大于任何一个子节点的键值时为最大堆，当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆。

3. 堆节点和数组索引关系

为了更加形象，我们常用带数字的圆圈和线条来表示二叉堆等，但其实都是用数组来表示的。如果根节点在数组中的位置是1，第n个位置的子节点则分别在2n和2n+1位置上。这一点很重要，在算法实现中，不可忽视，堆数据的存储，总是从数组的下标1开始。

对于给定的某个结点的下标i，可以很容易的计算出这个结点的父结点、孩子结点的下标，而且计算公式很漂亮很简约（i表示的是数组中的第几个，对应的数组索引号+1）：

PARENT(i)

return 小于或等于i/2的最大整数

LEFT-CHILD(i)

return 2i

RIGHT-CHILD(i)

return 2i+1

下面用一个图来形象描述一下堆与数组的关系。

4. 如何将一个节点所在的堆变成最大堆

程序中，不可能所有的堆都天生就是最大堆，为了更好的使用堆这一数据结构，我们可能要人为地构造最大堆。

如何将一个杂乱排序的堆重新构造成最大堆，它的主要思路是：

a. 从上往下，将父节点与子节点依次比较。

b. 如果父节点最大则进行下一步循环。

c. 如果子节点更大，则将子节点与父节点位置互换，并进行下一步循环。

d. 重复a-c的步骤

下面的例子，需要两步才能将节点2所在的堆整个堆排序成最大堆

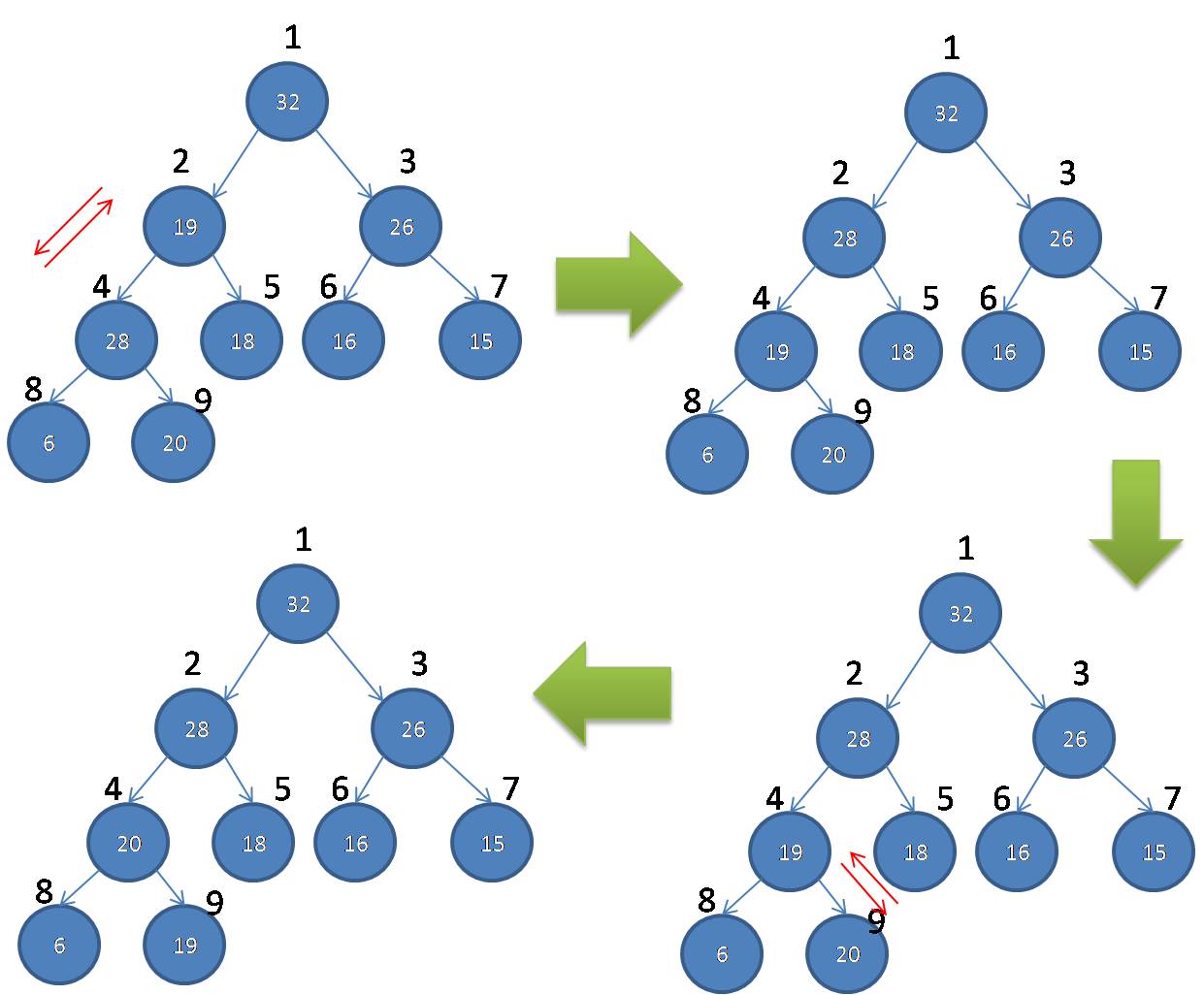
下面，通过MAX-HEAPIFY（A，i）的伪代码，展示上述堆排序的逻辑：

MAX-HEAPIFY(A, i)

l=LEFT-CHILD(i)                              　　　　 #LEFT-CHILD(i) = 2i

r=RIGHT-CHILD(i)                             　　　　#RIGHT-CHILD(i)=2i+1

if l<=A.hsize and A[l]>A[i]                             #A.hsize表示A中堆元素的个数

largest=l

else

　largest=i

if r<=A.hsize and A[r]>A[largest]

largest=r

if largest != i

exchange A[i] with A[largest]

　　　 MAX-HEAPIFY(A, largest)

对于这个MAX-HEAPIFY伪代码，java代码实现为：

/**
 * @author "shihuc"
 * @date   2017年3月22日
 */
package heapSort;

/**
 * @author chengsh05
 *
 */
public class MaxHeapify {

    static int hsize = ;

    /**
     * @param args
     */
    public static void main(String[] args) {

        int A[] = new int [] {, ,,,,,,,,};
        /*
         * 堆数据元素的个数，在这个例子中是数组长度 - 1
         */
        hsize = A.length - ;
        MaxHeapify mh = new MaxHeapify();

        /*
         * 注意，取父节点序号时，必须从1开始取。
         * 这里，主要是用来测试maxHeapify函数，对任何入口的效果。
         */
        for(int i = ; i<hsize; i++){
            mh.maxHeapify(A, i, hsize);
        }

        for(int i = ; i<A.length; i++){
            System.out.print(A[i] + ", ");
        }
    }

    /**
     * 获取当前节点i的左孩子节点在堆数据数组中的序号
     *
     * @param i 父节点序号
     * @return 左孩子节点序号
     */
    private int heapLeft(int i) {
        return *i;
    }

    /**
     * 获取当前节点i的右孩子节点在堆数据数组中的序号
     *
     * @param i 父节点序号
     * @return 右孩子节点序号
     */
    private int heapRight(int i) {
        return *i + ;
    }

    /**
     * 将堆A中的数据进行位置a,b上的数字交换
     *
     * @param A 堆数据数组
     * @param a 原始数据序号
     * @param b 待交换数据序号
     */
    public void exchange(int A[], int a, int b) {
        A[a] = A[a] ^ A[b];
        A[b] = A[b] ^ A[a];
        A[a] = A[a] ^ A[b];
    }

    /**
     * 将当前堆调整成为一个最大堆。
     *
     * @param A 待调整的堆数据数组
     * @param i 当前的父节点序号
     * @param heapSize 堆的元素个数
     */
    public void maxHeapify(int A[], int i, int heapSize){
        int larger = -;
        int l = heapLeft(i);
        int r = heapRight(i);
        if (l <= heapSize && A[l] > A[i]){
            larger = l;
        }else{
            larger = i;
        }
        if (r <= heapSize && A[r] > A[larger]){
            larger = r;
        }
        if (larger != i){
            exchange(A, i, larger);
            maxHeapify(A, larger, heapSize);
        }
    }
}

基于已有的MAX-HEAPIFY(A,i)来构建一个方法，能对所有的节点对应的堆数据结构进行调整，让这个A堆数据成为最大堆。

回顾一下上面的图示，其总共有9个结点，取小于或等于9/2的最大整数为4，从4+1，4+2，一直到n都是该树的叶子结点。这个现象，这对任意n都是成立的。

下面是构建一个最大堆的伪代码：

BUILD-MAX-HEAP(A)

A.hsize=A.length

for i=小于或等于A.length/2的最大整数 downto 1

MAX-HEAPIFY(A, i)

上面的伪代码，对应的图示流程如下图：

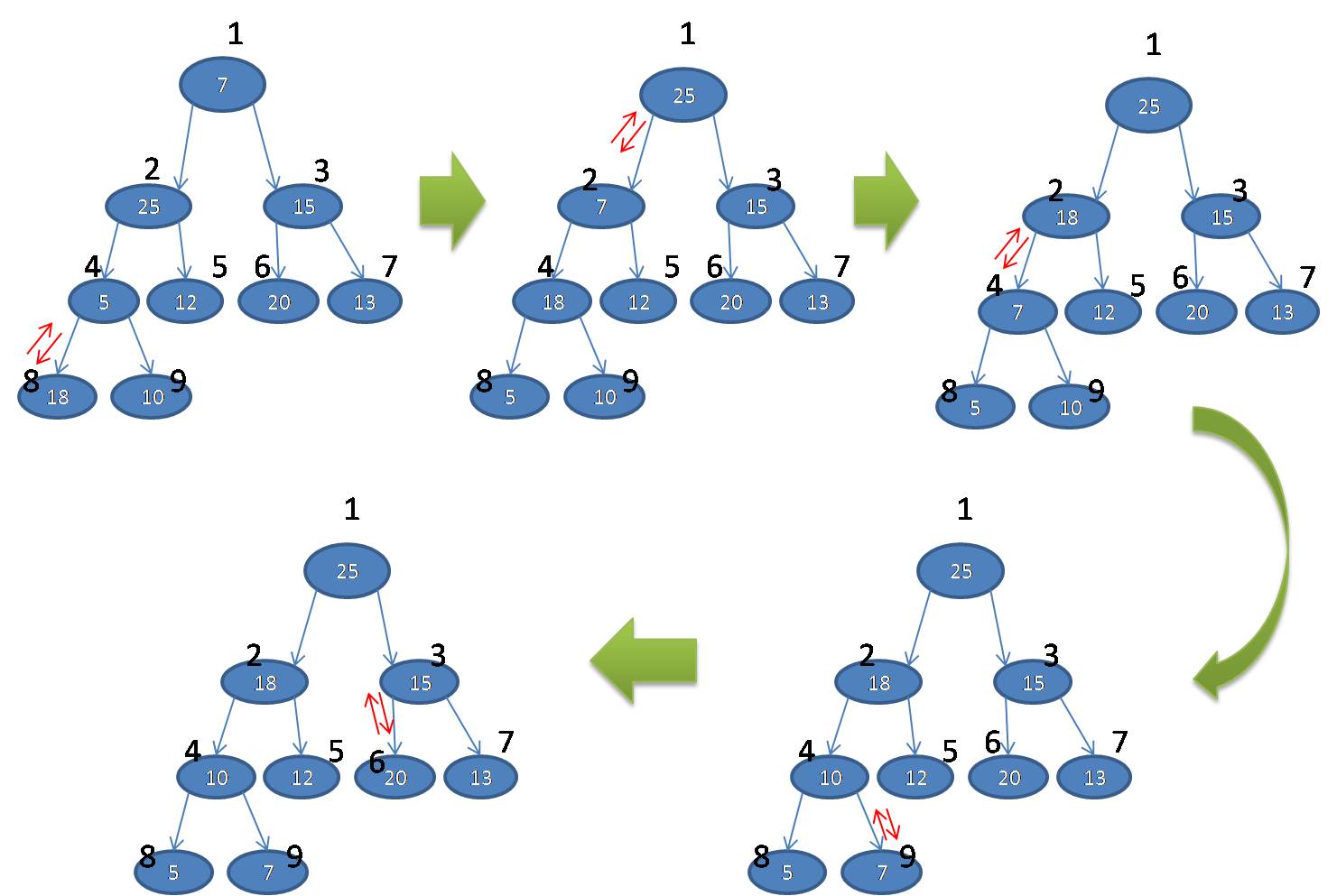
构建最大堆的java实现代码：

/**
 * @author "shihuc"
 * @date   2017年3月22日
 */
package heapSort;

/**
 * @author chengsh05
 *
 */
public class BuildMaxHeap {

    /**
     * @param args
     */
    public static void main(String[] args) {
        //int A[] = new int[] {0, 7,25,15,5,12,20,13,18,10};
        int A[] = new int [] {, ,,,,,,,,};
        BuildMaxHeap bmh = new BuildMaxHeap();
        bmh.buildMaxHeap(A, A.length-);
        for(int i=; i<A.length; i++){
            System.out.print(A[i] + ", ");
        }
    }

    private int getStartIdx(int len) {
        return (int)Math.floor(len/);
    }

    public void buildMaxHeap(int A[], int heapSize){
        MaxHeapify mh = new MaxHeapify();
        for(int i=getStartIdx(A.length); i>=; i--){
            mh.maxHeapify(A, i, heapSize);
        }
    }
}

其中MaxHeapify类，就是前述步骤中实现的类。

5. 堆排序实现

所谓的堆排序算法，先通过前面的BUILD-MAX-HEAP(A)将输入数组A[1...n]建成最大堆，其中n=A.length。而数组中的元素总在根结点A[1]中，通过把它与A[n]进行互换，就能将该元素放到正确的位置。基于上面前几部的理论分析，将堆调整成为最大堆后，A[1]的值总是堆中的最大值。

如何让原来根的子结点仍然是最大堆呢，可以通过从堆中去掉结点n，而这可以通过减少A.hsize来间接的完成。但这样一来新的根节点就违背了最大堆的性质，因此仍然需要调用MAX-HEAPIFY(A,1)，从而在A[1...n−1]上构造一个新的最大堆。

通过不断重复这一过程，直到堆的大小从n−1一直降到2即可。

实现步骤：

a. 通过BUILD-MAX-HEAP(A)构建最大堆

b. 将A[1]与A[x]交换，其中x取值范围[A.length, 2]降序取值。

c. 调整A.hsize = A.hsize - 1

d. 调用MAX-HEAPIFY(A,1)

e. 若x大于2，跳转到b处，继续后续步骤。

上述过程的伪代码如下：

HEAPSORT(A)

BUILD-MAX-HEAP(A)

for i=A.length downto 2

exchange A[1] with A[i]

A.heap-size=A.heap-size-1

                   MAX-HEAPIFY(A,1)

下面就用一个例子，结合上述伪代码，形象的介绍堆排序的过程。待排序的堆：9,18,21,23,222,121,234,90,211

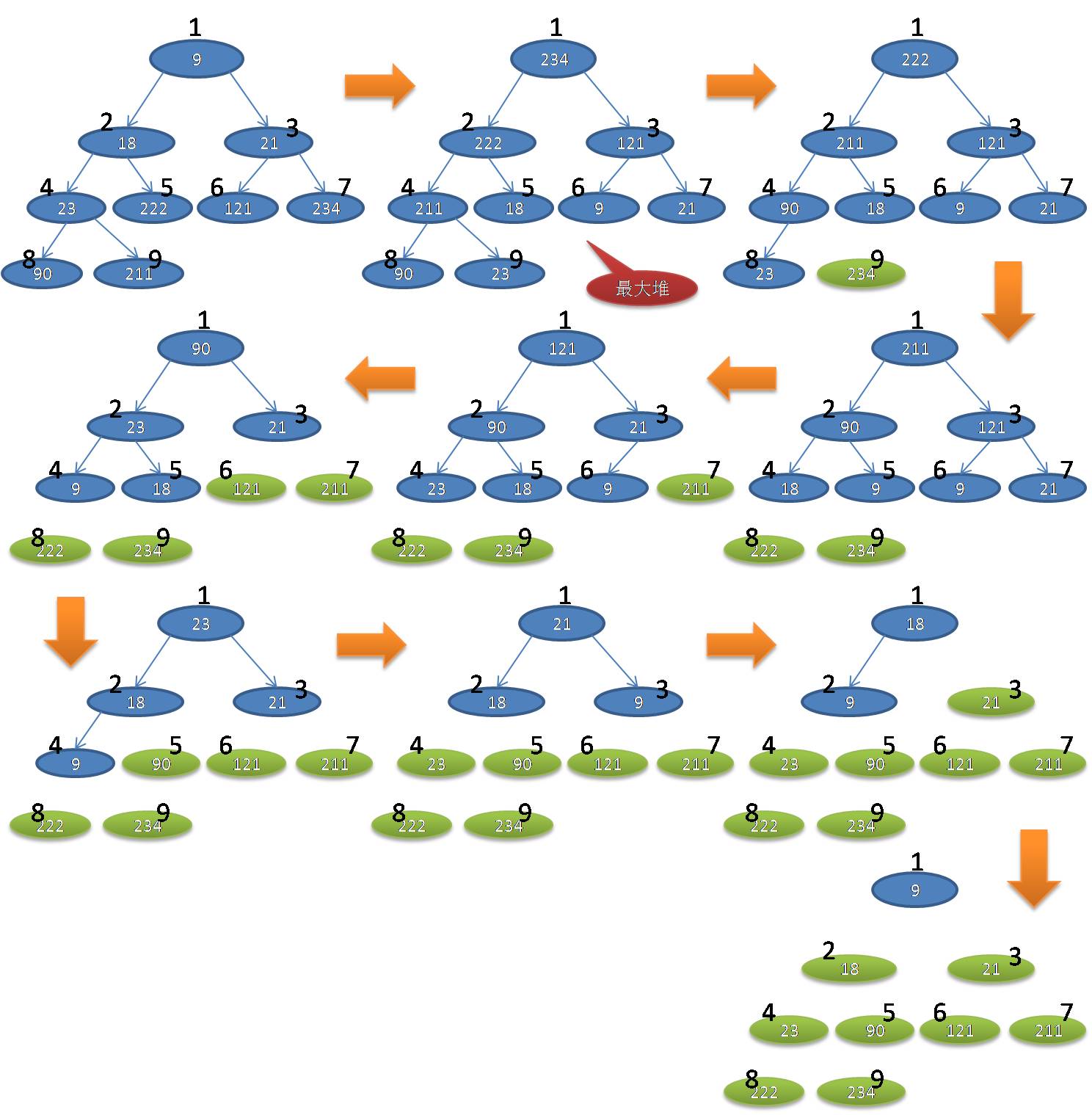
经过上述堆排序后，得到的排序后的结果为：9,18,21,23,90,121,211,222,234

针对上述堆排序的伪代码，其对应的java代码实现：

/**
 * @author "shihuc"
 * @date   2017年3月23日
 */
package heapSort;

import java.io.File;
import java.io.FileNotFoundException;
import java.util.Scanner;

/**
 * @author chengsh05
 *
 * 堆排序，主要实现思路：
 * a. 通过BUILD-MAX-HEAP(A)构建最大堆
 * b. 将A[1]与A[x]交换，其中x取值范围[A.length, 2]降序取值。
 * c. 调整A.hsize = A.hsize - 1
 * d. 调用MAX-HEAPIFY(A,1)
 * e. 若x大于2，跳转到b处，继续后续步骤。
 *
 */
public class HeapSort {

    /**
     * @param args
     */
    public static void main(String[] args) {
        File file = new File("./src/heapSort/sample.txt");
        Scanner sc = null;
        try {
            sc = new Scanner(file);
            int N = sc.nextInt();
            for(int i=; i<N; i++){
                int S = sc.nextInt();
                int A[] = new int[S+];
                for(int j=; j<S; j++){
                    A[j+] = sc.nextInt();
                }
                print(A, i, "is going to sort...");
                heapSort(A);
                print(A, i, "has been sorted....");
            }
        } catch (FileNotFoundException e) {
            e.printStackTrace();
        } finally {
            if(sc != null){
                sc.close();
            }
        }
    }

    /**
     * 用来打印输出堆中的数据内容。
     *
     * @param A 堆对应的数组
     * @param idx 当前是第几组待测试的数据
     * @param info 打印中输出的特殊信息
     */
    private static void print(int A[], int idx, String info){
        System.out.println(String.format("No. %02d %s ====================== ", idx, info));
        for(int i=; i<A.length; i++){
            System.out.print(A[i] + ", ");
        }
        System.out.println();
    }

    /**
     * 堆排序的具体实现过程
     *
     * @param A 待排序的堆
     */
    public static void heapSort(int A[]){
        BuildMaxHeap bmh = new BuildMaxHeap();
        MaxHeapify mh = new MaxHeapify();
        int hsize = A.length - ;
        /*
         * 实现步骤（a）
         * 将当前待排序的堆构建成一个最大堆
         */
        bmh.buildMaxHeap(A, hsize);
        print(A, , "*****");
        /*
         * 实现步骤（e）
         * 下面的for循环，就是在重复步骤b-d，直到堆长度为1
         */
        for(int i=A.length - ; i>=; i--){
            /*
             * 实现步骤（b）
             * 将堆结构中数组下标为1的数据与堆尾的数据互换位置
             */
            mh.exchange(A, i, );
            /*
             * 实现步骤（c）
             * 调整堆的实际长度。每次调整堆成最大堆并将堆的root节点取出后，原始堆的长度将减小1
             */
            hsize--;
            /*
             * 实现步骤（d）
             * 调用MAX-HEAPIFY（A，1）函数重新调整新堆为最大堆
             */
            mh.maxHeapify(A, , hsize);
            print(A, hsize, "~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~");
        }
    }
}

其中，sample.txt的测试数据为：

输出结果为：

No.  is going to sort... ======================
, , , , , , ,
No.  ***** ======================
, , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , ,
No.  has been sorted.... ======================
, , , , , , ,
No.  is going to sort... ======================
, , , , , , , , , ,
No.  ***** ======================
, , , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , , ,
No.  has been sorted.... ======================
, , , , , , , , , ,
No.  is going to sort... ======================
, , , , , , , , , , ,
No.  ***** ======================
, , , , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , , , ,
No.  has been sorted.... ======================
, , , , , , , , , , ,
No.  is going to sort... ======================
, , , , , , ,
No.  ***** ======================
, , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , ,
No.  has been sorted.... ======================
, , , , , , ,
No.  is going to sort... ======================
, , , , , , , , ,
No.  ***** ======================
, , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , ,
No.  ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ======================
, , , , , , , , ,
No.  has been sorted.... ======================
, , , , , , , , , 

结合上述的测试例以及打印输出的内容，对于理解堆排序应该是很容易的事情了，虽然麻烦了点。但是思路非常清晰易懂。其实也是一种选择排序的思路。

其时间复杂度为O（nlogn）。属于不稳定排序。至于什么是不稳定，自己看相关资料吧。