CompareTo 基于的排序算法

CompareTo 基于的排序算法(高级排序)

这个是今天学习MapReduce时发现的，自定义类后实现了WritableComparable<>接口后实现了接口中的compareTo方法，返回>1或者<1则会自动进行排序的方法。

然后特别好奇，查了查，学习下做一个总结。

首先说明 实现CompareTo方法的是使用了Collections.sort()和Arrays.sort()底层得算法，是timsort算法，插入排序和归并排序的高级合并 .

详情：https://blog.csdn.net/yangzhongblog/article/details/8184707

而这2个方法在底层实现时,使用到了object1.compareTo(object2)这种方法进行判断谁大谁小,从而调整数组,最终给你返回有序的集合，两个方法的排序算法实现有归并排序和快速排序。

详细将一下：归并排序是属于递归中的一种，而快速排序是是属于高级排序的，与其同时的 还有希尔排序，划分，基数排序。但最常用的还是快速排序。这里详解一下技术排序，归并排序我则在记录递归是将其一并总结。所以我来详解一下这个高级排序

高级排序

希尔排序：

    首次介绍下，希尔排序是基于插入排序的。插入排序利用临时变量比较和存储数据，交换位置来排序，所以虽然不是每个数据项都移动，但是数据项平均移动了n/2个位置，一共是n的平方/2次复制，插入排序的执行效率是O(N的平方).插入排序复制的次数太多，即数据项之间交换数据次数较多。希尔则避免了这个点。

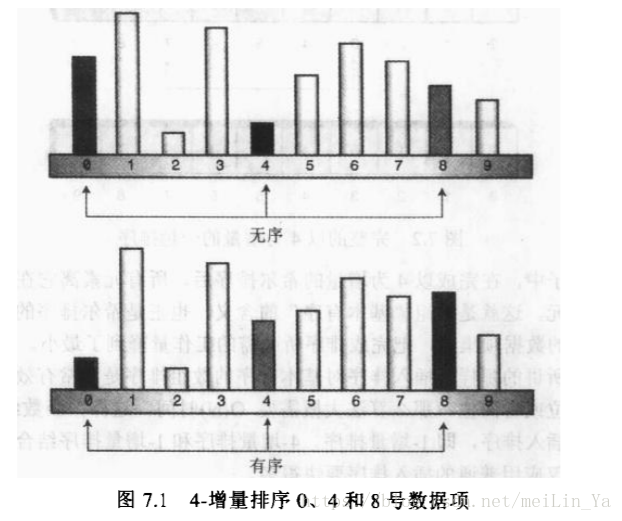
n-增量排序：通过加大插入排序中的元素之间的间隔。n：是指元素之间的间隔几个元素

我们来看一下主要的 4- 增量排序的放的排序过程。所有元素在离它最终的有序序列中的位置相差不到两个单元，做到了数据的基本有序，希尔则是做到了数据的基本有序，通过创建这种交错的内部有序的数据项集合，把完成排序所需的工作降调到最小

那么我们来研究一下这个间隔，这个间隔到底是使用多少为合适，可以将希尔的作用发挥到及至。以及间隔的选用。

间隔是通过数组得到大小进行变化的。比如1000个数据，间隔则为364-->121-->40-->13-->4-->1 这个间隔序列是通过递归计算出来的

谈希尔适合的排序环境：

这里是我的个人见解，如有更好的见解，欢迎一起讨论！！！

希尔排序适合中量数据的基本有序排序，少量数据使用插入排序进行更为稳定。

走开走开~~代码来了

package AdvancedRanking.ShellSort;

public class ArraySh {

    //数组
    private long[] theArray;

    //数组长度
    private int nElems;

    public ArraySh(int max) {
        theArray = new long[max];
        nElems = 0;
    }

    public void insert(long value) {
        theArray[nElems] = value;
        nElems++;
    }

    public void display() {
        System.out.print("A=");
        for (int j = 0; j < nElems; j++) {
            System.out.print(theArray[j] + " ");
        }
        System.out.println("");
    }

    public void shellSort() {
        int inner, outer;
        long temp;

        //初始时元素之间的间隔
        int h = 1;
        while (h <= nElems / 3) {
            h = h * 3 + 1;
        }

        while (h > 0) {
            for (outer = h; outer < nElems; outer++) {
                temp = theArray[outer];
                inner = outer;
                while (inner > h - 1 && theArray[inner - h] >= temp) {
                    theArray[inner] = theArray[inner - h];
                    System.out.println(theArray[inner]);
                    inner -= h;
                }
                theArray[inner] = temp;
            }
            //结束时元素之间的间隔
            h = (h - 1) / 3;
        }
    }

    public static void main(String[] args) {
        int maxSize = 10;
        ArraySh arr = new ArraySh(maxSize);

        for (int j = 0; j < maxSize; j++) {
            long n = (int) (Math.random() * 99);
            arr.insert(n);
        }
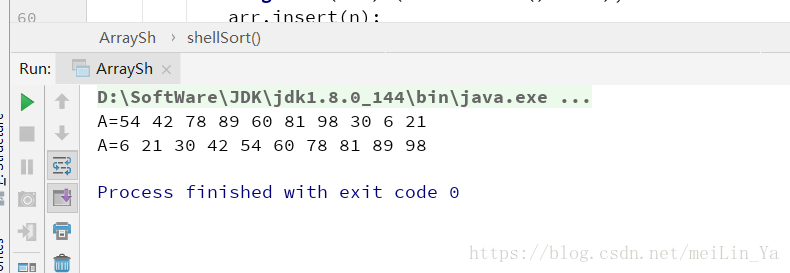
        arr.display();
        arr.shellSort();
        arr.display();
    }
}

二.划分

package AdvancedRanking.PartitionSort;

public class ArrayPar {

    private long[] theArray;
    private int nElems;

    public ArrayPar(int max) {
        theArray = new long[max];
        nElems = 0;
    }

    public void insert(long value) {
        theArray[nElems] = value;
        nElems++;
    }

    public int size() {
        return nElems;
    }

    public void display() {
        System.out.print("A=");
        for (int j = 0; j < nElems; j++) {
            System.out.print(theArray[j] + " ");
        }
        System.out.println("");
    }

    public int partitionIt(int left, int right, long pivot) {
        int leftPtr = left - 1;
        int rightPtr = right + 1;
        while (true) {
            //最大得
            while (leftPtr < right && theArray[++leftPtr] > pivot) ;
            //最小的
            while (rightPtr > left && theArray[--rightPtr] > pivot) ;

            if (leftPtr > rightPtr) {
                break;
            } else {
                swap(leftPtr, rightPtr);
            }
        }
        return leftPtr;
    }

    public void swap(int dex1, int dex2) {
        long temp;
        temp = theArray[dex1];
        theArray[dex1] = theArray[dex2];
        theArray[dex2] = temp;
    }

    public static void main(String[] args) {
        int maxSize = 10;
        ArrayPar arr = new ArrayPar(maxSize);
        for (int j = 0; j < maxSize; j++) {
            long n = (int) (Math.random() * 199);
            arr.insert(n);
        }
        arr.display();
        long piovt = 99;
        System.out.print("Piovt is " + piovt);
        int size = arr.size();

        int partDex = arr.partitionIt(0, size - 1, piovt);
        System.out.println(", Partition is at index " + partDex);
        arr.display();
    }
}

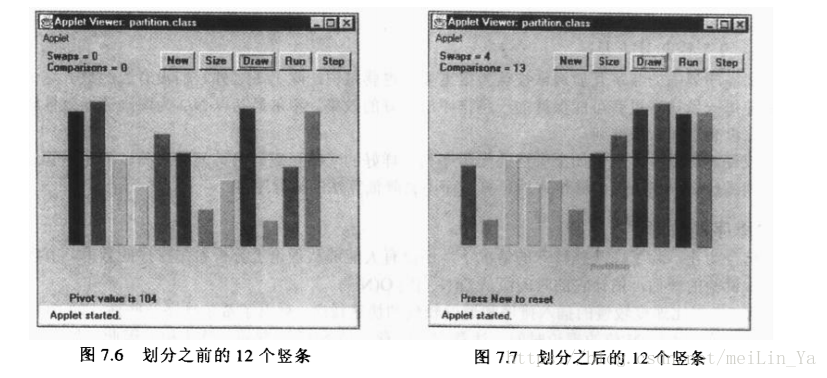
划分算法是由两个指针开始工作的，两个指针分别指向数据的两头leftPtr初始化是在第一个数据项的左边的一位，rightPtr是在最后一个数据项的右边一位。他们分别要-1  +1

  //找小于于piovt
 while (leftPtr < right && theArray[++leftPtr] > pivot) ;
   //找小于pivot
  while (rightPtr > left && theArray[--rightPtr] > pivot) ;

划分算法运行时间为O(N)，他其中的piovt枢纽，根据枢纽来移动指针和交换数据位置，虽然交换次数少，但是比较次数多。100个数大约交换25次，102次的比较。

快速排序：