POJ 2976 3111（二分-最大化平均值）

POJ 2976

题意

给n组数据ai,bi，定义累计平均值为：

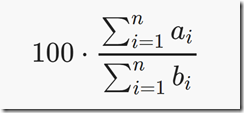
现给出一个整数k，要求从这n个数中去掉k个数后，最大累计平均值能有多大？(四舍五入到整数)

思路

取n−k个数，使得累计平均值最大。

定义C(x)表示能否取得n−k个数，使得累计平均值≥x。然后二分搜索最大的x。

可以这样判断可行性：

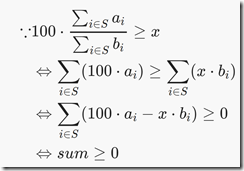
只需要从大到小选取n−k个(100⋅ai−x⋅bi)并求和sum，根据sum≥0来判断（上述的S表示n−k个元素下标的集合）

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;
typedef long long ll;
int n, k;
ll a[1000 + 4], b[1000 + 4];
double c[1000 + 4];
bool C(double x) { // 检验取出的n-k个数的累计平均值是否能>=x
	for (int i = 0; i < n; ++i)    c[i] = a[i] * 100 - x*b[i];
	sort(c, c + n);
	double sum = 0;
	for (int i = 0; i < n - k; ++i) sum += c[n - i - 1];
	return sum >= 0;
}
void solve() {
	double lb = 0, ub = 1000000000000000.0;
	for (int i = 0; i < 100; ++i) { // 精度10e-30
		double mid = (ub + lb) / 2.0;
		if (C(mid)) lb = mid; // 半闭半开区间[lb, ub)
		else ub = mid;
	}
	printf("%.f\n", floor(lb + 0.5)); // 四舍五入
}
int main()
{
	while (cin >> n >> k) {
		if (n == k && n == 0) break;
		for (int i = 0; i < n; ++i) cin >> a[i];
		for (int i = 0; i < n; ++i) cin >> b[i];
		solve();
	}
	return 0;
}

POJ 3111

题意

给出n个珠宝的vi和wi，从中选出k个珠宝，使得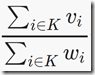最大，求出这k个珠宝的序列。

思路

同上，排序时需记录序号。

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;
const double EPS = 1e-6;
int n, k;
int v[100000 + 5], w[100000 + 5];
struct Remian{
	double c;
	int id;
	bool operator<(const Remian&b) const {
		return c > b.c;
	}
} remain[100000 + 5];
bool C(double x) {
	for (int i = 0; i < n; ++i) {
		remain[i].c = v[i] - w[i] * x;
		remain[i].id = i + 1; // 记录宝珠编号
	}
	sort(remain, remain + n);
	double sum = 0.0;
	for (int i = 0; i<k; ++i) sum += remain[i].c;
	return sum >= 0;
}
void solve() {
	double lb = 0.0, ub = 1000000000000000.0;
	//while (ub - lb > EPS) { // 精度1e-6
	for(int i=0; i<80; ++i) { // 精度10e-30
		double mid = (lb + ub) / 2.0;
		if (C(mid)) lb = mid; // 半闭半开区间[lb, ub)
		else ub = mid;
	}
	for (int i = 0; i < k; ++i) printf(i == 0 ? "%d" : " %d", remain[i].id);
	printf("\n");
}
int main()
{
	scanf("%d%d", &n, &k);
	for (int i = 0; i < n; ++i) scanf("%d%d", &v[i], &w[i]);
	solve();
	return 0;
}