Codeforces 827E Rusty String - 快速傅里叶变换 - 暴力

Grigory loves strings. Recently he found a metal strip on a loft. The strip had length n and consisted of letters "V" and "K". Unfortunately, rust has eaten some of the letters so that it's now impossible to understand which letter was written.

Grigory couldn't understand for a long time what these letters remind him of, so he became interested in the following question: if we put a letter "V" or "K" on each unreadable position, which values can the period of the resulting string be equal to?

A period of a string is such an integer d from 1 to the length of the string that if we put the string shifted by d positions to the right on itself, then all overlapping letters coincide. For example, 3 and 5 are periods of "VKKVK".

Input

There are several (at least one) test cases in the input. The first line contains single integer — the number of test cases.

There is an empty line before each test case. Each test case is described in two lines: the first line contains single integer n(1 ≤ n ≤ 5·105) — the length of the string, the second line contains the string of length n, consisting of letters "V", "K" and characters "?". The latter means the letter on its position is unreadable.

It is guaranteed that the sum of lengths among all test cases doesn't exceed 5·105.

For hacks you can only use tests with one test case.

Output

For each test case print two lines. In the first line print the number of possible periods after we replace each unreadable letter with "V" or "K". In the next line print all these values in increasing order.

Example

input

3
 
5
V??VK
 
6
??????
 
4
?VK?

output

2
3 5
6
1 2 3 4 5 6
3
2 3 4

Note

In the first test case from example we can obtain, for example, "VKKVK", which has periods 3 and 5.

In the second test case we can obtain "VVVVVV" which has all periods from 1 to 6.

In the third test case string "KVKV" has periods 2 and 4, and string "KVKK" has periods 3 and 4.

---

　　题目大意 给定一个只包含通配符'?'和'v'，'K'的串，询问所有可能的循环节长度。

　　首先一个事实就是如果x是可能的循环节，那么2x，3x也一定是。(证明是显然的)

　　因此可以根据这个愉快的事实进行暴力(似乎出题人在题解的Comments中表示对数据出水了感到歉意)

　　思路大概就是暴力check如果可行就把它的倍数都标为可行的。

Code

 /**
  * Codeforces
  * Problem#827E
  * Accepted
  * Time: 265ms
  * Memory: 988k
  */
 #include <bits/stdc++.h>
 using namespace std;
 typedef bool boolean;

 const int lim = 5e5;

 int n;
 char str[lim + ];
 boolean app[];
 boolean able[lim + ];

 inline void init() {
     scanf("%d", &n);
     gets(str);
     gets(str);
 }

 inline boolean check(int len) {
     for(int i = ; i < len; i++) {
         char should = str[i];
         for(int j = i + len; j < n; j += len) {
             if(should != '?' && str[j] != '?' && should != str[j])    return false;
             if(str[j] != '?')    should = str[j];
         }
     }
     return true;
 }

 inline void solve() {
     app[] = app[] = false;
     for(int i = ; i < n; i++) {
         switch(str[i]) {
             case 'V':
                 app[] = true;
                 break;
             case 'K':
                 app[] = true;
                 break;
         }
     }
     if(!app[] && !app[]) {
         printf("%d\n", n);
         for(int i = ; i <= n; i++)
             printf("%d%c", i, (i == n) ? ('\n') : (' '));
         return;
     }
     int res = ; //, cnt = 0;
     for(int i = ; i <= n; i++)
         if(!able[i] && check(i))// && (++cnt))
             for(int j = i; j <= n; j += i)
                 res += !able[j], able[j] = true;
     printf("%d\n", res);
     for(int i = ; i <= n; i++)
         if(able[i]) {
             printf("%d ", i);
             able[i] = false;
         }
     putchar('\n');
 //    fprintf(stderr, "%dms counted %d times\n", clock(), cnt);
 }

 int T;
 int main() {
     scanf("%d", &T);
     while(T--) {
         init();
         solve();
     }
     return ;
 }

Rusty String(Brute force)

　　然后假设没有这个通配符应该怎么用bitset, 多项式乘法之类的做(因为每个位置除了通配符，只有V或K，而且因为有通配符的存在，所以KMP就不能抓过来用了)

　　首先根据KMP的思想，如果存在长度为k的循环节那么存在长度为(n - k)的公共前后缀。

　　所以我们可以把这个串右移k位然后check，最后判一下特殊情况。

　　为了更快地进行check，所以，我们设A数组中A[I]为1当且仅当s[I] == 'v'，B[i]为1当且仅当s[i] == 'K'。

　　初步可行的条件是并且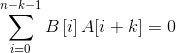

　　然后为了能够顺利地进行下一步，我们设A'[i] = A[n - i - 1]。于是你会发现两边A'的下标和B的和是一个定值，而且范围不相交。因此我们可以把A'数组和B数组当成两个多项式的系数数组，然后进行FFT。

　　最开始说的特殊情况是指类似于存在某一个i使得s[i] != s[i + 2k]并且s[i + k] == '?'。

　　首先可以初步地将一些循环节判断为不可行，对于看似没有问题的循环节长度，我们还需要check它的倍数中有没有被标记为不可行的，如果存在它就不可行(这样做的话就可以把以上的特殊情况处理掉)。

　　因为数据没有卡暴力，我深深地感受到什么是暴力碾压正解。

Code

 /**
  * Codeforces
  * Problem#827
  * Accepted
  * Time: 311ms
  * Memory: 68200k
  */
 #include <bits/stdc++.h>
 using namespace std;
 typedef bool boolean;

 template<typename T>
 class Complex {
     public:
         T r;
         T v;

         Complex(T r = , T v = ):r(r), v(v) {        }

         Complex operator + (Complex b) {
             return Complex(r + b.r, v + b.v);
         }

         Complex operator - (Complex b) {
             return Complex(r - b.r, v - b.v);
         }

         Complex operator * (Complex b) {
             return Complex(r * b.r - v * b.v, r * b.v + v * b.r);
         }

         Complex operator / (double x) {
             return Complex(r / x, v / x);
         }
 };

 const int N =  << ;
 const double pi = acos(-);
 const double eps = 0.5;

 inline void Rader(Complex<double> *f, int len) {
     for(int i = , j = len >> , k; i < len - ; i++) {
         if(i < j)
             swap(f[i], f[j]);
         for(k = len >> ; j >= k; j -= k, k >>= );
         if(j < k)
             j += k;
     }
 }

 inline void fft(Complex<double> *f, int len, int sign) {
     Rader(f, len);
     for(int l = ; l <= len; l <<= ) {
         Complex<double> wn(cos( * pi / l), sin( * pi * sign / l)), u, v;
         int hl = l >> ;
         for(int i = ; i < len; i += l) {
             Complex<double> w(, );
             for(int j = ; j < hl; j++, w = w * wn) {
                 u = f[i + j], v = w * f[i + j + hl];
                 f[i + j] = u + v, f[i + j + hl] = u - v;
             }
         }
     }
     if(sign == -)
         for(int i = ; i < len; i++)
             f[i] = f[i] / len;
 }

 int n, len;
 char str[];
 Complex<double> A[N], B[N];

 inline void init() {
     scanf("%d", &n);
     gets(str);
     gets(str);
     for(len = ; len < (n << ); len <<= );
     memset(A, , sizeof(Complex<double>) * (len + ));
     memset(B, , sizeof(Complex<double>) * (len + ));
     for(int i = ; i < n; i++) {
         if(str[i] == 'V')
             A[n - i - ].r = ;
         else if(str[i] == 'K')
             B[i].r = ;
     }
 }

 boolean bad[N];
 int res = ;
 inline void solve() {
     fft(A, len, );
     fft(B, len, );
     for(int i = ; i < len; i++)    A[i] = A[i] * B[i];
     fft(A, len, -);
     memset(bad, false, sizeof(boolean) * (n + ));
 //    for(int i = 1; i < n; i++)
 //        if(A[n - i - 1].r >= eps || A[n + i - 1].r >= eps)
 //            bad[i] = true;
     for(int i = ; i < len; i++)
         if(A[i].r >= eps)
             bad[abs(i - n + )] = true;
     for(int i = ; i < n; i++)
         if(!bad[i])
             for(int j = i << ; j < n; j += i)
                 if(bad[j]) {
                     bad[i] = true;
                     break;
                 }
     int res = ;
     for(int i = ; i <= n; i++)
         if(!bad[i])
             res++;
     printf("%d\n", res);
     for(int i = ; i <= n; i++) {
         if(!bad[i])
             printf("%d ", i);
     }
     putchar('\n');
 }

 int T;
 int main() {
     scanf("%d", &T);
     while(T--) {
         init();
         solve();
     }
     return ;
 }