【Learning】 动态树分治

简介

　　动态树分治整体上由点分治发展而来。

　　点分治是统计树上路径，而动态树分治用来统计与点有关的树上路径，比如多次询问某一些点到询问点的距离和。

　　前置知识就是点分治。

做法

　　众所周知，点分树（点分治中重心组成的树）的深度是$O(lgn)$的。

　　要统计树上的路径，等价为统计经过每个点的路径。那么就统计经过每个重心的路径。

　　

　　拿一道题目来讲比较具体：BZOJ4012。有一棵带点权边权的树，多次询问$(u,l,r)$，表示询问点权在$[l,r]$内的点到$u$的距离和。

　　比如一个重心$u$，其管辖范围为$S_u$，询问的点$q$在$v$子树内：

　　

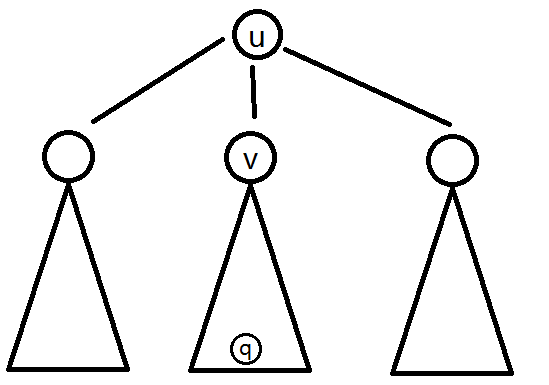
　　那么应该用其它两棵子树内所有符合的点到$u$的距离和 + $q$到$u$的距离乘上其它子树内符合的点的个数，就是经过这个重心的答案。

　　注意到我们需要容斥：用$u$的信息斥去$v$的信息才能得到划线部分的值，这和点分治的做法大致相同。

　　方便点来说，$v$子树的重心$v'$，除了要像$u$一样记录$S_v'$内所有点到它的信息，还要记录$S_v'$内所有点到$u$的信息，也就是到点分父亲的信息。原理上是和点分治一模一样的容斥，只不过为了方便，应该把这个信息放在子树的重心记录。

　　完整做法如下：

　　　　对于点分树上的每一个重心$u$：记其管辖范围为$S_u$。

　　　　求出$S_u$内每一个点到$u$的距离值。

　　　　对$S_u$内每一个点按照点权由小至大排序，求出排序后距离值的前缀和。

　　　　对$u$的每一个后继$v$，若$v$子树的重心为$v'$，求出$S_v'$内所有点到$u$的距离值，对它们按照点权由小至大排序，求出排序后距离值的前缀和。

　　　　calc1(u,l,r)表示求$S_u$内权值为$[l,r]$的点到$u$的距离和，由于已经按照权值排序，又有前缀和，可以二分得出$l$和$r$的位置，返回前缀和。

　　　　calc2(u,l,r)表示求$S_u$内权值为$[l,r]$的点到$u$的点分父亲的距离和，求法同上。

　　　　size(u,l,r)表示求$S_u$内权值为$[l,r]$的点有多少个，求法同上二分。

　　　　dis(x,y)表示求原树上$x$~$y$的距离。

　　　　

　　　　查询$(u,l,r)$

　　　　对于$u$和$u$的所有点分树祖先，记为$x$，设$u$在$x$的$y$子树中：

　　　　$ans+=dis(u,x)*[size(x,l,r)-size(y,l,r)]+calc1(x,l,r)-calc2(y,l,r)$

　　　　

 #include <cstdio>
 #include <algorithm>
 #include <vector>
 #define mp make_pair
 using namespace std;
 typedef long long ll;
 typedef pair<int,int> pii;
 const int N=,INF=,Bas=;
 int n,q,A,a[N],h[N],tot; //权值和边
 int pre[N][Bas],dep[N],dist[N]; //倍增lca  点到根节点的深度和距离
 int cut[N],fa[N];//点分区块断点，点分树父亲
 int size[N],mins,minu; //找重心
 struct Edge{int v,next,w;}g[N*]; //树边
 vector<pii> lis[N],lisf[N]; //每个重心的数据列表 每个重心相对于点分父亲的数据列表
 vector<ll> sum[N],sumf[N]; //每个重心列表按权值排序后距离前缀和 每个重心相对于点分父亲的列表按权值排序后距离前缀和
 inline int rd(){
     int x=;
     char c;
     while((c=getchar())<''||c>'');
     x=c-'';
     while(''<=(c=getchar())&&c<='') x=x*+c-'';
     return x;
 }
 inline int min(int x,int y){return x<y?x:y;}
 inline int max(int x,int y){return x>y?x:y;}
 inline void swap(int &x,int &y){int t=x;x=y;y=t;}
 inline void addEdge(int u,int v,int w){
     g[++tot].v=v; g[tot].w=w; g[tot].next=h[u]; h[u]=tot;
     g[++tot].v=u; g[tot].w=w; g[tot].next=h[v]; h[v]=tot;
 }
 void predfs(int u,int fa,int Dep,int Dist){//计算11行的数组
     dep[u]=Dep;
     dist[u]=Dist;
     pre[u][]=fa;
     for(int i=;i<Bas;i++) pre[u][i]=pre[pre[u][i-]][i-];
     for(int i=h[u],v;i;i=g[i].next)
         if((v=g[i].v)!=fa)
             predfs(v,u,Dep+,Dist+g[i].w);
 }
 int getlca(int a,int b){
     if(dep[a]<dep[b]) swap(a,b);
     for(int i=Bas-;i>=;i--)
         if(dep[pre[a][i]]>=dep[b]) a=pre[a][i];
     if(a==b) return a;
     for(int i=Bas-;i>=;i--)
         if(pre[a][i]!=pre[b][i]) a=pre[a][i],b=pre[b][i];
     return pre[a][];
 }
 int getdis(int x,int y){
     int lca=getlca(x,y);
     return dist[x]-dist[lca]+dist[y]-dist[lca];
 }
 void dfs1(int u,int fa){//找重心
     size[u]=;
     for(int i=h[u],v;i;i=g[i].next)
         if(!cut[v=g[i].v]&&v!=fa){
             dfs1(v,u);
             size[u]+=size[v];
         }
 }
 void dfs2(int u,int fa,int all){//找重心
     int maxt=;
     for(int i=h[u],v;i;i=g[i].next)
         if(!cut[v=g[i].v]&&v!=fa){
             dfs2(v,u,all);
             if(size[v]>maxt) maxt=size[v];
         }
     if(all-size[u]>maxt) maxt=all-size[u];
     if(maxt<mins) mins=maxt,minu=u;
 }
 int getroot(int u){//找重心
     mins=INF; minu=;
     dfs1(u,);
     dfs2(u,,size[u]);
     return minu;
 }
 void collect(int u,int fa,int dis,int st,int type){//收集数据至重心st的列表
     if(!type) lis[st].push_back(mp(a[u],dis));
     else lisf[st].push_back(mp(a[u],dis));
     for(int i=h[u],v;i;i=g[i].next)
         if(!cut[v=g[i].v]&&v!=fa)
             collect(v,u,dis+g[i].w,st,type);
 }
 int find(vector<pii> &u,int x,int type){//以权值为关键字，lowerbound或upperbound x的位置
     int l=,r=u.size()-,mid;
     while(l<=r){
         mid=(l+r)>>;
         if((!type&&x<=u[mid].first)||(type&&x<u[mid].first)) r=mid-;
         else l=mid+;
     }
     return l;
 }
 ll calc(vector<pii> &u,vector<ll> &s,int l,int r,int type){//计算列表在l~r的点的距离和或个数
     int pos1=find(u,l,);
     int pos2=find(u,r,)-;
     if(pos2<pos1) return ;
     if(pos1==){
         if(!type) return s[min(u.size()-,pos2)];
         else return min(u.size()-,pos2)+;
     }
     if(!type)
         return s[min(u.size()-,pos2)]-s[max(,pos1-)];
     else
         return min(u.size()-,pos2)-max(,pos1)+;
 }
 int solve(int rt,int faedge){//预处理
     int u=getroot(rt);
     collect(u,,,u,);
     sort(lis[u].begin(),lis[u].end());
     ll x=;
     for(int i=,sz=lis[u].size();i<sz;i++){
         x+=lis[u][i].second;
         sum[u].push_back(x);
     }
     if(faedge){
         collect(rt,,faedge,u,);
         sort(lisf[u].begin(),lisf[u].end());
         x=;
         for(int i=,sz=lisf[u].size();i<sz;i++){
             x+=lisf[u][i].second;
             sumf[u].push_back(x);
         }
     }
     cut[u]=;
     for(int i=h[u],v;i;i=g[i].next)
         if(!cut[v=g[i].v])
             fa[solve(v,g[i].w)]=u;
     return u;
 }
 ll query(int st,int u,int l,int r,ll sonsum,int sonsize){//询问
     ll ret=;
     if(fa[u]) ret=query(st,fa[u],l,r,calc(lisf[u],sumf[u],l,r,),calc(lisf[u],sumf[u],l,r,));
     ret+=1LL*getdis(st,u)*(calc(lis[u],sum[u],l,r,)-sonsize)+calc(lis[u],sum[u],l,r,)-sonsum;
     return ret;
 }
 int main(){
     n=rd(); q=rd(); A=rd();
     for(int i=;i<=n;i++) a[i]=rd();
     for(int i=,u,v,w;i<n;i++){
         u=rd();v=rd();w=rd();
         addEdge(u,v,w);
     }
     predfs(,,,);
     solve(,);
     int u,l,r;
     ll ans=;
     while(q--){
         u=rd(); l=rd(); r=rd();
         l=(l+ans)%A; r=(r+ans)%A;
         if(l>r) swap(l,r);
         ans=query(u,u,l,r,,);
         printf("%lld\n",ans);
     }
     return ;
 }