数据结构 之 二叉堆(Heap)

|
index |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
value |
|
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
|
|
|
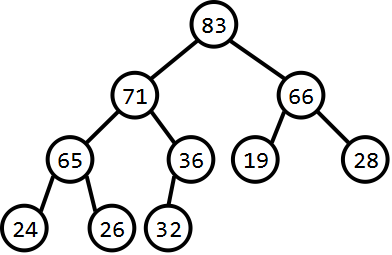

声明:
int findMax()
下沉操作:
在给出具体如何建堆的操作之前,我们可以考察一下具体应该怎样去实现。

|
index
|
83
|
11
|
6
|
15 |
36
|
19
|
|
value
|
1
|
2
|
3
|
4
|
5
|
6
|

堆排序的关键在于将最大值元素交换到数组尾端,重新进行堆维护操作。依次循环操作,即可以得到排序的数组。
|
23
|
1
|
16
|
9
|
54
|

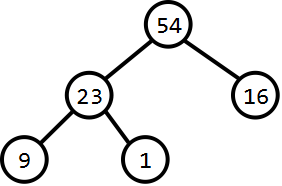
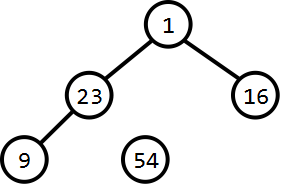
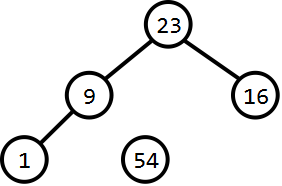

|
1
|
9
|
16
|
23
|
54
|
从而完成了对数组的排序。
插入insertHeap():该操作同优先队列(priority queue)中的push操作。


删除deleteHeapMax():相当于优先队列中的pop()操作。
|
查询操作
|
O(1)
|
|
堆维护操作
|
O(logN)
|
| 建堆操作 |
O(NlogN)
|
|
堆排序操作
|
O(NlogN)
|
数据结构 之 二叉堆(Heap)的更多相关文章
- D&F学数据结构系列——二叉堆
二叉堆(binary heap) 二叉堆数据结构是一种数组对象,它可以被视为一棵完全二叉树.同二叉查找树一样,堆也有两个性质,即结构性和堆序性.对于数组中任意位置i上的元素,其左儿子在位置2i上,右儿 ...
- 【算法与数据结构】二叉堆和优先队列 Priority Queue
优先队列的特点 普通队列遵守先进先出(FIFO)的规则,而优先队列虽然也叫队列,规则有所不同: 最大优先队列:优先级最高的元素先出队 最小优先队列:优先级最低的元素先出队 优先队列可以用下面几种数据结 ...
- 【数据结构与算法Python版学习笔记】树——利用二叉堆实现优先级队列
概念 队列有一个重要的变体,叫作优先级队列. 和队列一样,优先级队列从头部移除元素,不过元素的逻辑顺序是由优先级决定的. 优先级最高的元素在最前,优先级最低的元素在最后. 实现优先级队列的经典方法是使 ...
- 数据结构图文解析之:二叉堆详解及C++模板实现
0. 数据结构图文解析系列 数据结构系列文章 数据结构图文解析之:数组.单链表.双链表介绍及C++模板实现 数据结构图文解析之:栈的简介及C++模板实现 数据结构图文解析之:队列详解与C++模板实现 ...
- POJ 2010 - Moo University - Financial Aid 初探数据结构 二叉堆
考虑到数据结构短板严重,从计算几何换换口味= = 二叉堆 简介 堆总保持每个节点小于(大于)父亲节点.这样的堆被称作大根堆(小根堆). 顾名思义,大根堆的数根是堆内的最大元素. 堆的意义在于能快速O( ...
- 二叉堆(binary heap)
堆(heap) 亦被称为:优先队列(priority queue),是计算机科学中一类特殊的数据结构的统称.堆通常是一个可以被看做一棵树的数组对象.在队列中,调度程序反复提取队列中第一个作业并运行,因 ...
- 《数据结构与算法分析:C语言描述》复习——第五章“堆”——二叉堆
2014.06.15 22:14 简介: 堆是一种非常实用的数据结构,其中以二叉堆最为常用.二叉堆可以看作一棵完全二叉树,每个节点的键值都大于(小于)其子节点,但左右孩子之间不需要有序.我们关心的通常 ...
- Binary Heap(二叉堆) - 堆排序
这篇的主题主要是Heapsort(堆排序),下一篇ADT数据结构随笔再谈谈 - 优先队列(堆). 首先,我们先来了解一点与堆相关的东西.堆可以实现优先队列(Priority Queue),看到队列,我 ...
- 堆(Heap)和二叉堆(Binary heap)
堆(Heap) The operations commonly performed with a heap are: create-heap: create an empty heap heapify ...
随机推荐
- PS图层混合算法之六(差值,溶解, 排除)
差值模式: 查看每个通道中的颜色信息,比较底色和绘图色,用较亮的像素点的像素值减去较暗的像素点的像素值.与白色混合将使底色反相:与黑色混合则不产生变化. 排除模式可生成和差值模式相似的效果,但比差值模 ...
- Linux - /etc/passwd和/etc/shadow文件结构
/etc/passwd文件结构 1.账号名称: 就是账号啦!用来对应 UID 的.例如 root 的 UID 对应就是 0 (第三字段): 2.口令: 早期 U ...
- IP网际协议 - IP首部,IP路由选择,子网掩码
IP首部 4个字节的32 bit值以下面的次序传输:首先是0-7 bit,其次8-15 bit,然后1 6-23 bit,最后是24~31 bit.这种传输次序称作big endian字节序.由于T ...
- OpenCV分通道显示图片,灰度,融合,直方图,彩色直方图
代码有参考跟整合:没有一一列出出处 // split_rgb.cpp : 定义控制台应用程序的入口点. // #include "stdafx.h" #include <io ...
- Android开源经典项目
目前包括: Android开源项目第一篇--个性化控件(View)篇 包括ListView.ActionBar.Menu.ViewPager.Gallery.GridView.ImageView. ...
- UITableView设置单元格选中后只显示一个打勾的三种简单方法(仅供参考)
1.第一种方法:先定位到最后一行,若选中最后一行直接退出,否则用递归改变上次选中的状态,重新设置本次选中的状态. - (UITableViewCell*)tableView:(UITableView* ...
- 如何将windows格式的图标作为os x应用程序的图标
刚由windows转为os x的同学可能知道,在os x下我们想改变一个app的图标异常简单,直接打开该app的简介,然后将图标文件拖入简介窗口左上角图标方框即可.但是很多童鞋下载了一些图标文件后发现 ...
- solr研磨之性能调优
作者:战斗民族就是干 转载请注明地址:http://www.cnblogs.com/prayers/p/8982141.html 本篇文章我们来了解一下solr的性能方面的调优,分为Schema优化 ...
- 零基础自学Python十天,写了一款猜数字小游戏,附源码和软件下载链接!
自学一门语言最重要的是要及时给自己反馈,那么经常写一些小程序培养语感很重要,写完可以总结一下程序中运用到了哪些零散的知识点. 本程序中运用到的知识点有: 1.输入输出函数 (input.print) ...
- txtbook简单HTML可读化改造
一般来讲下载的txtbook在notepad或者之类的文本编辑器下的阅读体验不是很好,PC上面专门装个txt阅读器好像有点杀鸡用牛刀,可以用HTML简单处理一下就可以放在浏览器下爽快的阅读了,这个操作 ...
