跟着小菜学习RabbitMQ启动和基础（系列一）

前言

今天开始我们正式进入RabbitMQ系列学习，在这系列博客中也会发表.NET Core和EF Core文章，网上关于RabbitMQ例子比比皆是，我将综合网上所提供的信息并加上我个人的理解来详细介绍RabbitMQ，欢迎各位大佬指正我这个菜鸟。

RabbitMQ安装后启动

关于安装RabbitMQ就无需我再多言，网上例子比比皆是，这里只是列出在启动时可能存在的问题，我们从官网上下载并安装了对应应用程序后，都会有对应的操作快捷方式。

当安装完毕后，我们首先通过rabbitmqctl status命令来查看服务器状态。网上的所给服务器状态失败情况大部分原因可归纳为两个如下查看状态失败。

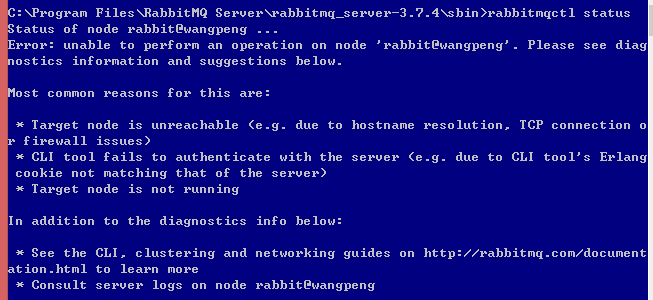
我们从上述第二张图中Current node details下三点可得知node name为rabbitmqcli41@wangpeng，@后面为我们电脑的计算机名称。而第二点和第三点得知此时Erlang cookie存在于C\Users\JeffckyWang文件目录下。为解决这个问题我们可首先从两个方面来快速定位问题，第一：保证C:\Windows和 C\Users\JeffckyWang下的.erlang.cookie要一致，如果不存在那就复制保证二者一致，如果依然不能解决问题，那就启用第二种方案。默认情况下安装RabbitMQ后会在服务中存在RabbitMQ，此时RabbitMQ的默认登录身份为本地账号，此时可能是账户不一致而导致，上述也有讲到根据第二张图中最后节点详细信息中第二点知，有效的用户账户为JeffckyWang，所以我们修改账户为JeffckyWang：

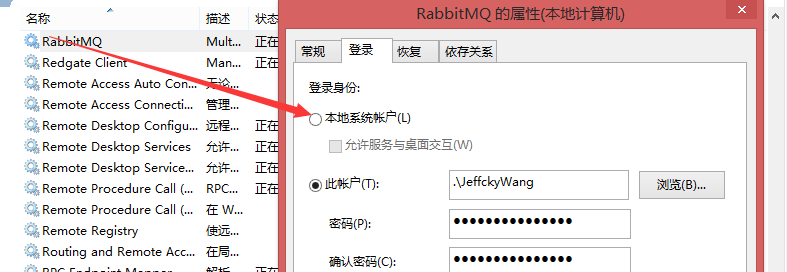
接下来再来运行rabbitmqctl status命令和rabbitmq-plugins enable rabbitmq_management命令启动RabbitMQ可视化界面。如果运行这两个命令没有出错，那么我们在浏览器中输入地址：http://localhost:15672，默认用户名和密码为guest，如下：

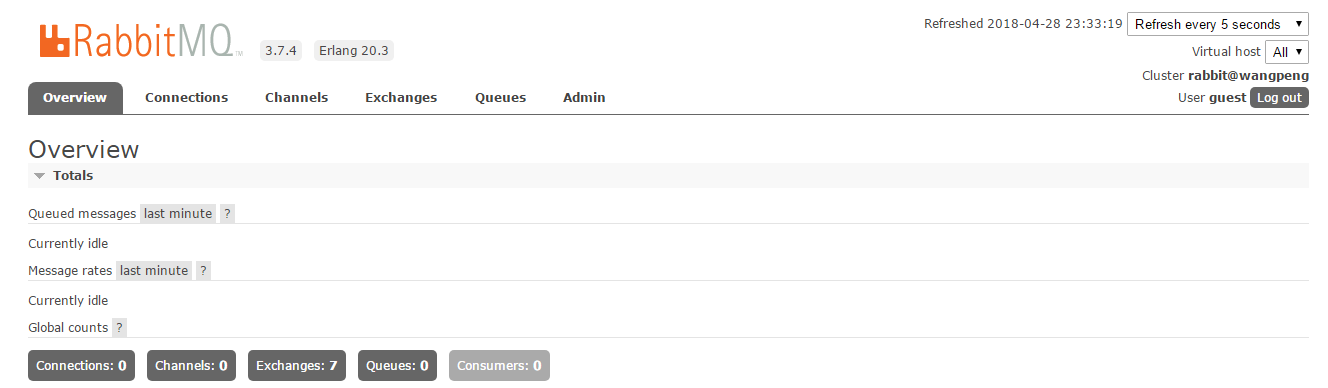
RabbitMQ介绍

消息传递是一种以可靠和可维护的方式解决不同系统之间通信的技术。我们可以有各种相互之间通信的平台比如Windows服务，基于Java servlet的Web服务，MVC Web应用程序等。消息传递旨在整合这些系统，以便它们可以以分离的方式交换信息即分布式。消息总线可能是消息传递基础结构中最重要的组件。它是协调在消息队列中发送和接收消息的机制。在此之前业界有许多解决消息传递的方法：Java消息传递服务，MSMQ，IBM MQ，但它们从未真正得到普及，因为基于这些技术的消息系统是复杂的，昂贵的，难以连接并且通常难以使用，而且他们没有遵循任何特定的消息传递标准;即每个供应商都有自己的标准，客户必须严格遵守。在小型项目中我们不需要用到事件总线，我们完全可采用代理调用接口的方式来进行，但是一旦项目大一点这个时候可能就需要考虑事件总线，为什么呢？我们拿常见用户注册可能需要用到发送邮件激活，对于当用户注册时，用户提交信息后调用代理接口来发送邮件，但是我们怎么能够保证代理是实时的呢，或者并发上来代理挂了，那么要发送的消息是不是就丢了呢？这将会造成重大事故，最重要的是这个操作是同步的，只有等发送完邮件回执时我们才能进行下一步操作，整个操作会造成堵塞，我们理想的情况是用户注册后，紧接着我们只需要发布一条激活邮件的消息，其他我们就不用再关心，完全不需要等待这个操作完成。

RabbitMQ是基于Erlang编程语言的高可用性开源消息框架。 “高可用性”意味着它在处理消息时不仅非常快速，而且还具有可扩展性。这是一个管理Web UI的服务，我们可以在多个服务器上进行安装。这些服务器然后作为一组消息代理一同启动。如果集群中的一台服务器出现故障，其他服务器仍然可以处理传入的消息。因此，它类似于部署在两台或更多台Web服务器上的Web应用程序，前端具有负载均衡器。默认情况下，RabbitMQ是实现高级消息队列协议（AMQP）的高可用性消息传递框架，AMQP是一个类似于HTTP的开放标准线级协议。它独立于任何特定的供应商，独立于任何特定的供应商这是最重要的一点，AMQP不是公司的专有协议，而是“在应用程序或组织之间传递业务信息的开放标准。它连接系统，为业务流程提供所需的信息，并可靠地传输实现其目标的指令。

总结

今天我们只是初略介绍了RabbitMQ，接下来我们正式进入RabbitMQ的学习，希望对您有些许帮助同时也能得到大佬们的批评指正，我们下节再会。