C_关于递归算法的几个例子

1.递归算法的定义：

2.递归与迭代的优劣

eg1：斐波那契数列：斐波那契数列（Fibonacci sequence），又称黄金分割数列、因数学家列昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……在数学上，斐波纳契数列以如下被以递归的方法定义：F(0)=1，F(1)=1, F(n)=F(n-1)+F(n-2)（n>=2，n∈N*）

 /*
     斐波那契数列 迭代实现        (打印出前40个)
 */
 #include <stdio.h>
 int main(){
     int i, arr[];
     arr[] = ;
     arr[] = ;
     printf("%d %d ",arr[],arr[]);
     for(i=; i<; i++){
         arr[i] = arr[i-] + arr[i-];
         printf("%d ",arr[i]);
     }
     printf("\n");

     return ;

 }

 /*
     斐波那契数列 递归实现    (打印出前40个)
 */
 #include <stdio.h>
 /*
 int fb(int n){
     if(n == 0){
         return 0;
     }else if(n == 1){
         return 1;
     }else{
         return fb(n-1) + fb(n-2);
     }
 }
 */

 int fb(int n){
     if(n<){
         return n == ? :;
     }else{
         return fb(n-) + fb (n-);
     }

 }

 int main(){
     int i;
     for(i=; i<; i++){
         printf("%d ",fb(i));
     }
     printf("\n");

     return ;
 }

eg2：阶乘：亦即n!=1×2×3×...×n。阶乘亦可以递归方式定义：0!=1，n!=(n-1)!×n。

 /*
     递归实现阶乘
     递归方式定义：0!=1，n!=(n-1)!×n。
 */

 #include <stdio.h>
 int fact(n){
     if(n == ){
         return ;
     }else{
         return fact(n-) * n;
     }
 }

 int main(){
     int n = ;
     printf("%d\n",fact(n));
     return ;
 }

eg3：

 #include <stdio.h>
 int print(){
     char a;
     scanf("%c", &a);
     if(a != '#'){
         print();
     }
     if(a != '#'){
         printf("%c",a);
     }
     return ;
 }
 int main(){
     print();
     printf("\n");
     return ;
 }

解题思路：

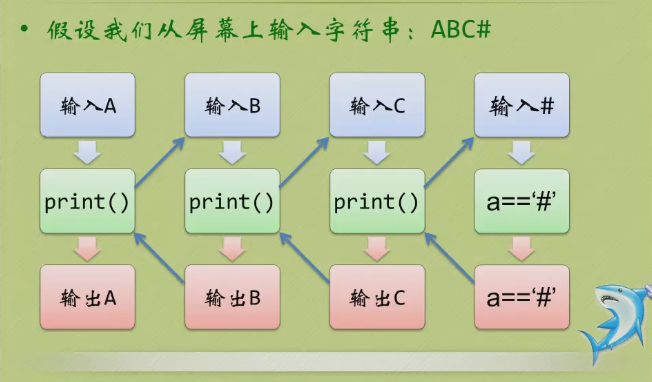
eg4：二分法查找

 /*
     二分法查找：迭代实现
 */
 #include <stdio.h>
 int main(){
     int arr[] = {,,,,,,,,,};
     int input, low, high, mid;
     low = ;
     high = ;
     mid = (low + high) / ;
     scanf("%d", &input);

     while(input != arr[mid]){
         if(input < arr[mid]){
             high = mid;
             mid = (low + high) / ;
         }else{
             low = mid;
             mid = (low + high) / ;
         }
     }
     printf("%d ",mid);/*输出要查找数字在数组中的下标*/
     return ;

 }

 /*
     二分法查找：递归实现
 */

 #include <stdio.h>
 int fun(int low, int high, int input, int arr[]){
     int mid;
     mid = (low + high) /;
     if(arr[mid] == input){
         return mid;
     }else{
         if(input < arr[mid]){
             high = mid;
             return fun( low, high, input, arr);
         }else{
             low = mid;
             return fun( low, high, input, arr);
         }
     }

 }
 int main(){
     int arr[] = {,,,,,,,,,};
     int input, low, high;
     low = ;
     high = ;
     scanf("%d", &input);
     printf("%d \n",fun(low, high, input, arr));/*输出要查找数字在数组中的下标*/
     return ;
 }