[leetcode]716. Max Stack 最大栈

Design a max stack that supports push, pop, top, peekMax and popMax.

1. push(x) -- Push element x onto stack.
2. pop() -- Remove the element on top of the stack and return it.
3. top() -- Get the element on the top.
4. peekMax() -- Retrieve the maximum element in the stack.
5. popMax() -- Retrieve the maximum element in the stack, and remove it. If you find more than one maximum elements, only remove the top-most one.

Example 1:

MaxStack stack = new MaxStack();
stack.push(5);
stack.push(1);
stack.push(5);
stack.top(); -> 5
stack.popMax(); -> 5
stack.top(); -> 1
stack.peekMax(); -> 5
stack.pop(); -> 1
stack.top(); -> 5

Note:

1. -1e7 <= x <= 1e7
2. Number of operations won't exceed 10000.
3. The last four operations won't be called when stack is empty.

题目

思路

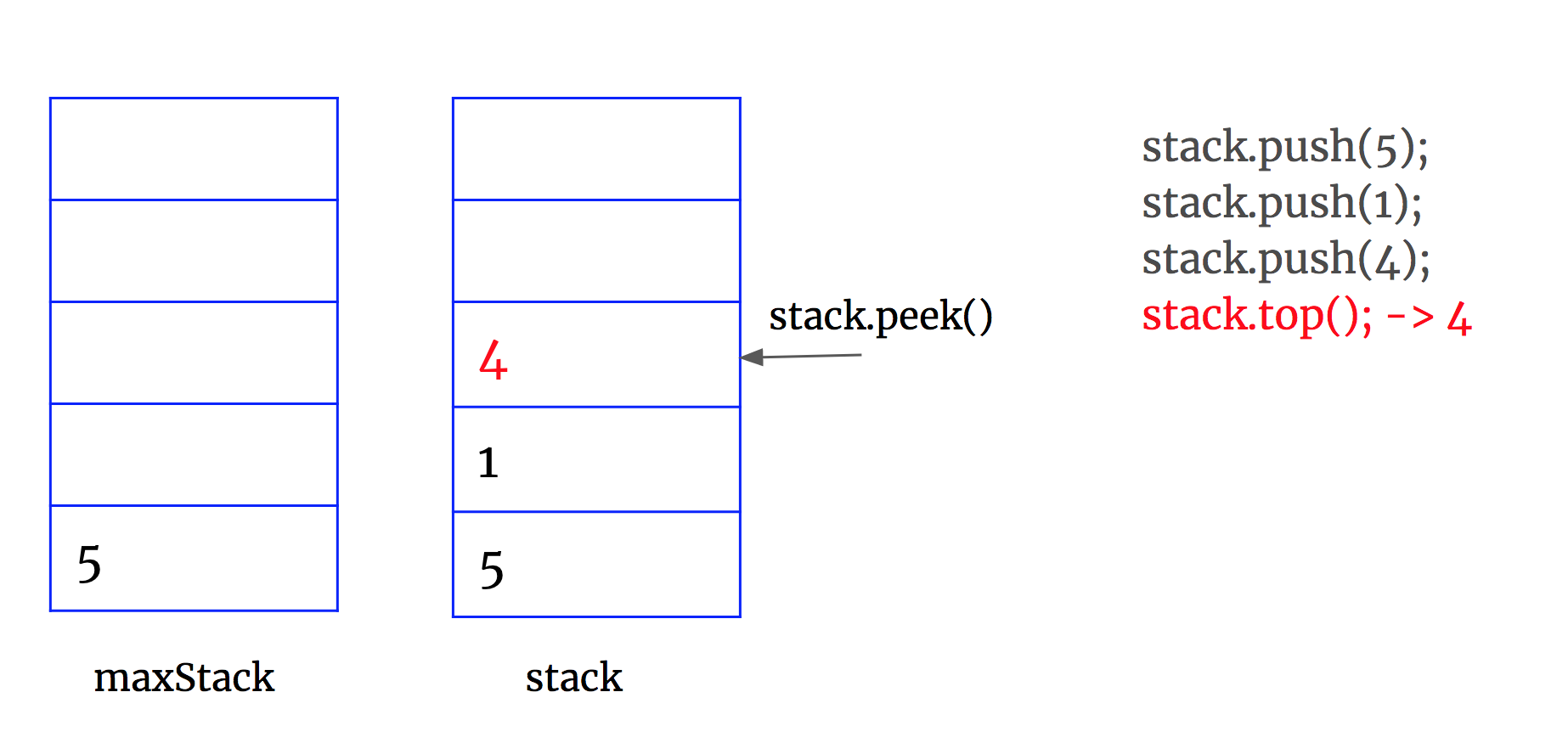
1.  maintain stack to track all the data

2. maintain maxStack to update current max, making sure that stack.size() == maxStack.size()

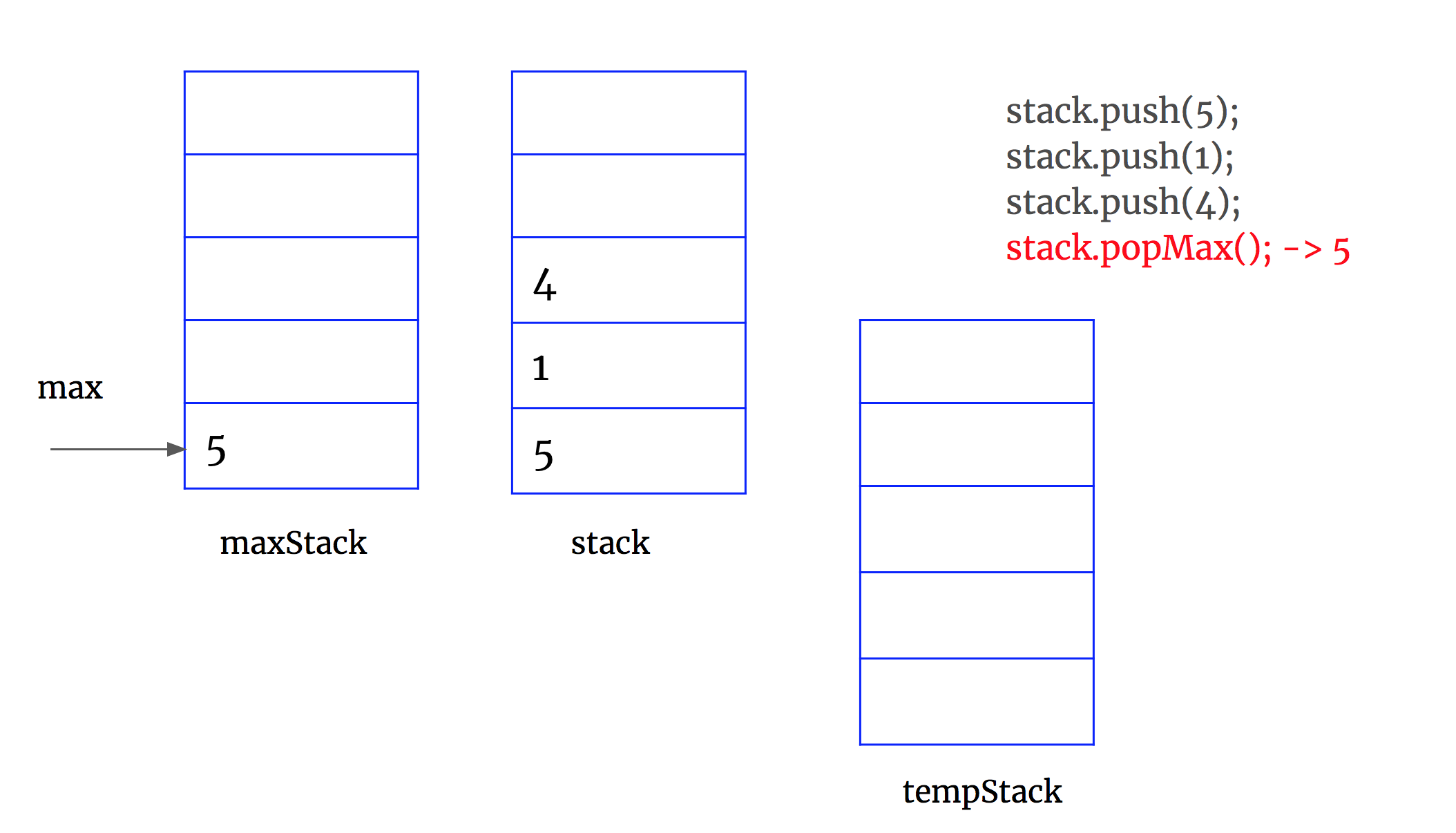
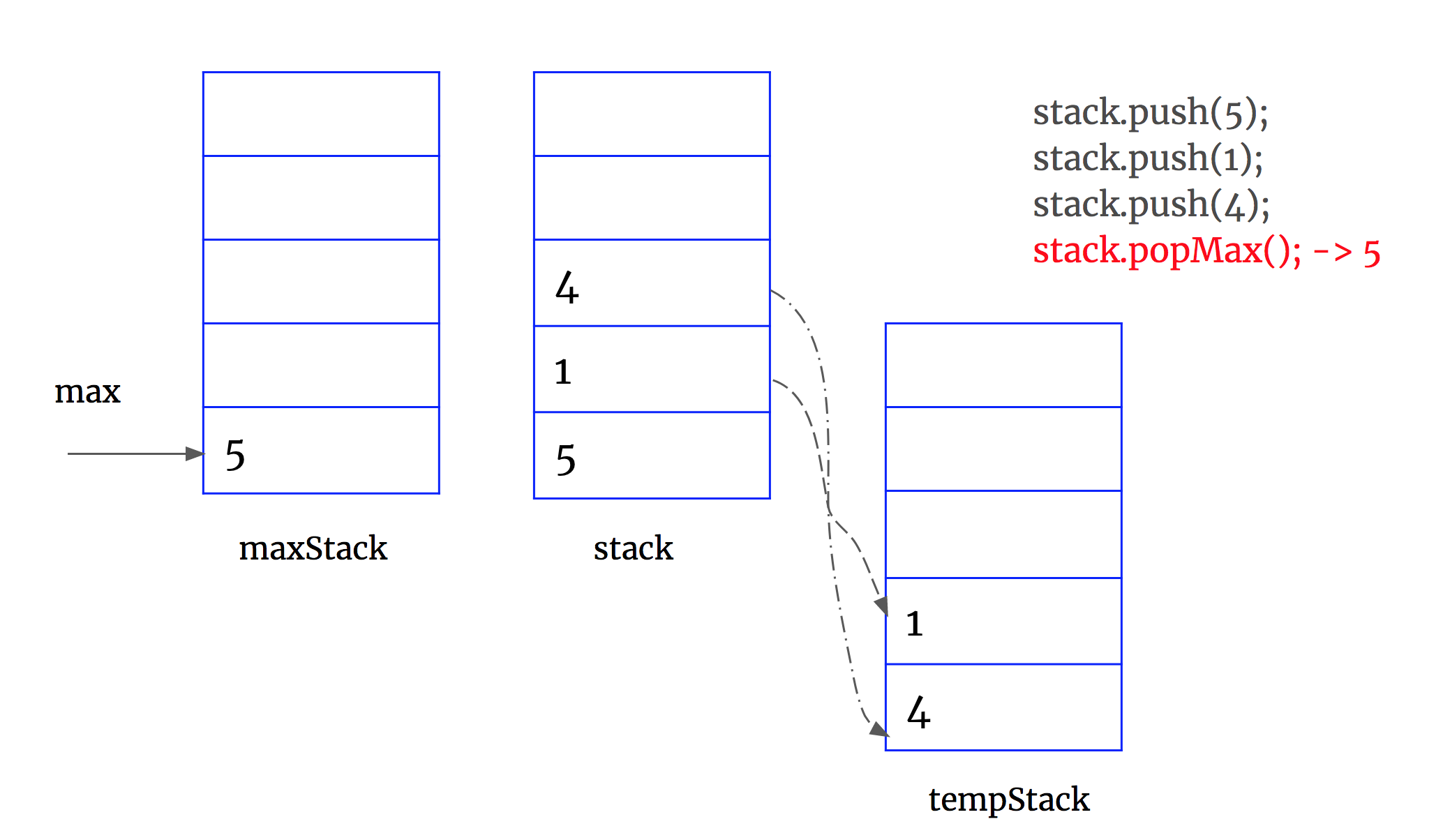
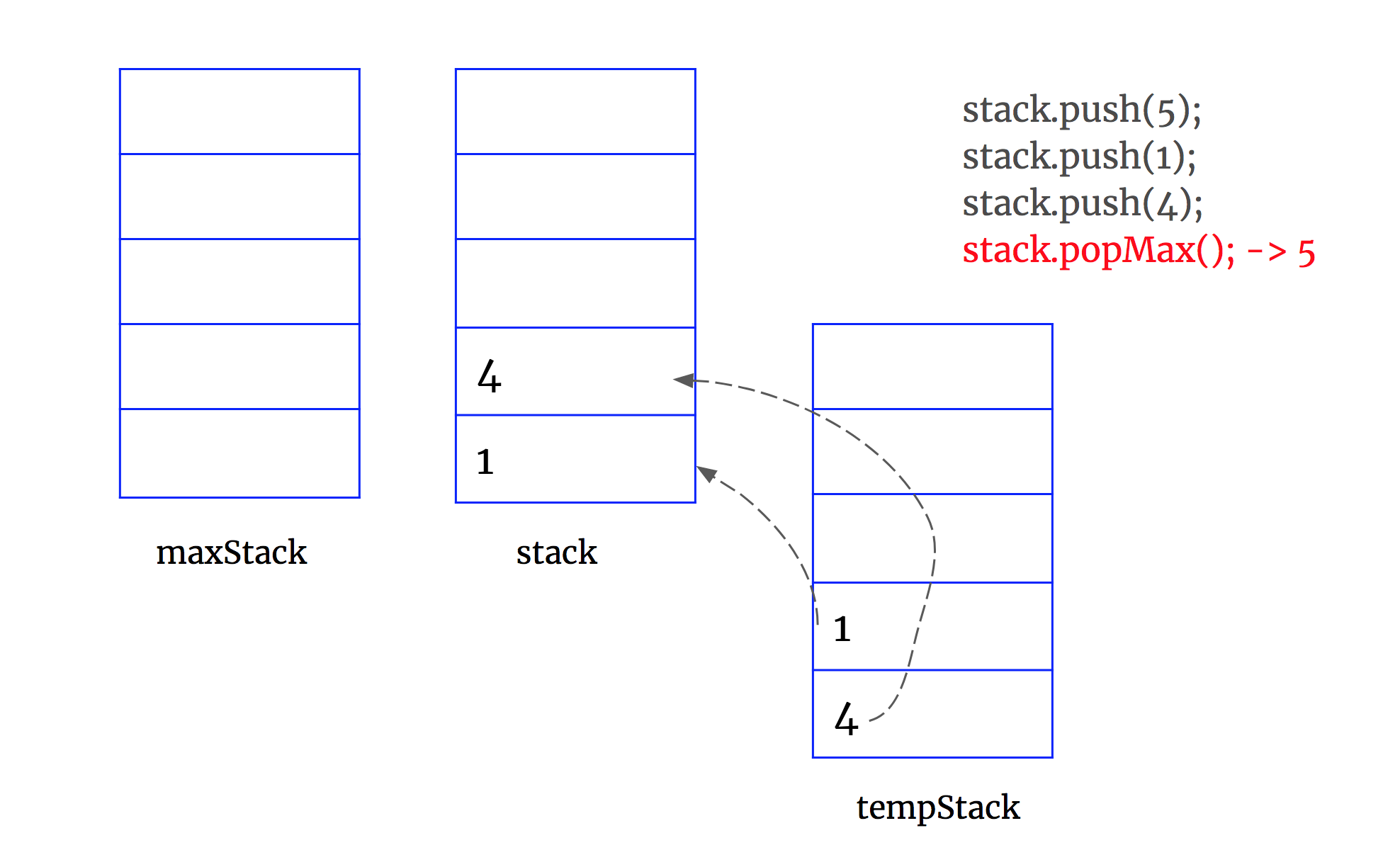
3. when popMax(), use tempStack to convert data. When push data back to stack, don't forget to update maxStack at the same time.

code

 class MaxStack {
     // maintain stack to track all the data
        Stack <Integer> stack  =  new Stack<Integer>();
     // maintain maxStack to update current max
     Stack <Integer> maxStack  =  new Stack<Integer>();

     public void push(int x) {
         // 保证stack和maxStack的元素数量一致， 即便 x == maxStack.peek(), 也会同时push到maxStack和stack
         if (maxStack.isEmpty() || x >= maxStack.peek()){
                 maxStack.push(x);
         }
         stack.push(x);
     }

     public int pop() {
        if (stack.peek().equals(maxStack.peek())){
                    maxStack.pop();
        }
        return stack.pop();
     }

     public int top() {
         return stack.peek();
     }

     public int peekMax() {
         return maxStack.peek();
     }

     public int popMax() {
             // maintain a tempStack to help convert data
             Stack <Integer> tempStack  =  new Stack<Integer>();

             int max  = maxStack.peek();
             // 1. push non-max item into tempStack
             while (!stack.peek().equals(maxStack.peek())){
                  tempStack.push(stack.pop());
             }
             stack.pop();
             maxStack.pop();

             //2. directly use push() we wrote, pushing items back in both stack and tempStack
             while(!tempStack.isEmpty()){
                     push(tempStack.pop());
             }
             return max;
     }
 }