二叉树、B树、B+树、B*树、LSM树

 

HBase 对于数据产品，底层存储架构直接决定了数据库的特性和使用场景。RDBMS（关系型数据库）使用 B树 及 B+树 作为数据存储结构。 HBase 使用 LSM树。 。

 

 

二叉树 

        所有节点至多拥有两个子节点。节点左指针指向小于其关键字的子树，右指针指向大于其关键字的子树；B树搜索，从根结点开始，如果查询的关键字与结点的关键字相等，那么就命中；

        

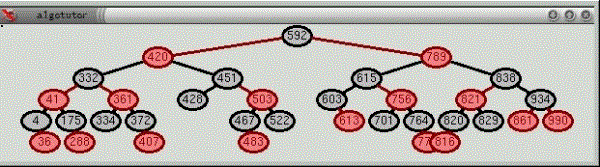
B+树

数据的读取速度因素

由于传统的机械磁盘具有快速顺序读写、慢速随机读写的访问特性，这个特性对磁盘存储结构和算法的选择影响甚大。

为了改善数据访问特性，文件系统或数据库系统通常会对数据排序后存储，加快数据检索速度，这就需要保证数据在不断更新、插入、删除后依然有序，传统关系数据库的做法是使用B+树，如图所示。

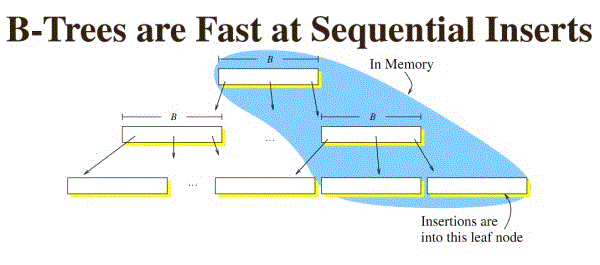
B树在插入的时候，如果是最后一个node,那么速度非常快，因为是顺序写。

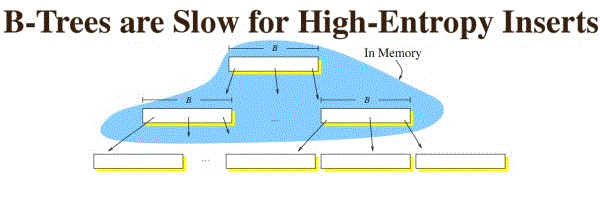
但如果有更新插入删除等综合写入，最后因为需要循环利用磁盘块，所以会出现较多的随机io.大量时间消耗在磁盘寻道时间上。

-----------------------------------------------------------------------------------------------------------------------------------

PS：B+树就是在B树基础上加两个规定  1.子结点只存指针，子结点存数据  2.所有子结点从左到右用双链表串起来

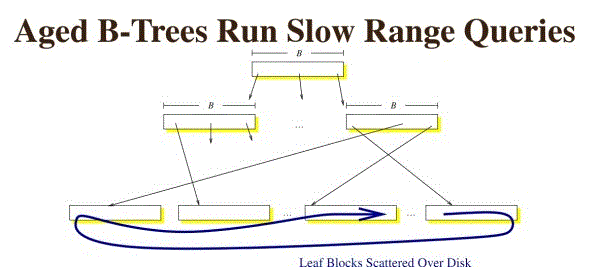
b+树原理，b+树在查询过程中应该是不会慢的，但如果数据插入比较无序的时候，比如先插入5 然后10000然后3然后800 这样跨度很大的数据的时候，就需要先“找到这个数据应该被插入的位置”，然后插入数据。这个查找到位置的过程，如果非常离散，那么就意味着每次查找的时候，他的子节点都不在内存中，这时候就必须使用磁盘寻道时间查找。更新基本与插入是相同的

LSM树 

简单来说，就是放弃磁盘读性能来换取写的顺序性。乍一看，似乎会认为读应该是大部分系统最应该保证的特性，所以用读换写似乎不是个好买卖。但别急，听我分析之  LSM树性能分析。

1.      内存的速度超磁盘1000倍以上。而读取的性能提升，主要还是依靠内存命中率而非磁盘读的次数

2.      写入不占用磁盘的io，读取就能获取更长时间的磁盘io使用权，从而也可以提升读取效率。

因此，虽然SSTable降低了了读的性能，但如果数据的读取命中率有保障的前提下，因为读取能够获得更多的磁盘io机会，因此读取性能基本没有降低，甚至还会有提升。而写入的性能则会获得较大幅度的提升，基本上是5~10倍左右。

LSM树 插入数据可以看作是一个N阶合并树。数据写操作（包括插入、修改、删除也是写）都在内存中进行，

数据首先会插入内存中的树。当内存树的数据量超过设定阈值后，会进行合并操作。合并操作会从左至右便利内存中树的子节点 与 磁盘中树的子节点并进行合并，会用最新更新的数据覆盖旧的数据（或者记录为不同版本）。当被合并合并数据量达到磁盘的存储页大小时。会将合并后的数据持久化到磁盘，同时更新父节点对子节点的指针。

LSM树 读数据 磁盘中书的非子节点数据也被缓存到内存中。在需要进行读操作时，总是从内存中的排序树开始搜索，如果没有找到，就从磁盘上的排序树顺序查找。

在LSM树上进行一次数据更新不需要磁盘访问，在内存即可完成，速度远快于B+树。当数据访问以写操作为主，而读操作则集中在最近写入的数据上时，使用LSM树可以极大程度地减少磁盘的访问次数，加快访问速度。

LSM树 删除数据 前面讲了。LSM树所有操作都是在内存中进行的，那么删除并不是物理删除。而是一个逻辑删除，会在被删除的数据上打上一个标签，当内存中的数据达到阈值的时候，会与内存中的其他数据一起顺序写入磁盘。 这种操作会占用一定空间，但是LSM-Tree 提供了一些机制回收这些空间。

作为存储结构，B+树不是关系数据库所独有的，NoSQL数据库也可以使用B+树。同理，关系数据库也可以使用LSM，而且随着SSD硬盘的日趋成熟及大容量持久存储的内存技术的出现，相信B+树这一"古老"的存储结构会再次焕发青春。

 

 

 

小结

二叉树：，每个结点只存储一个关键字，等于则命中，小于走左结点，大于走右结点；

二叉树，B树：多路搜索树，每个结点存储M/2到M个关键字，非叶子结点存储指向关键字范围的子结点； 所有关键字在整颗树中出现，且只出现一次，非叶子结点可以命中；

B+树：在B树基础上，为子结点增加链表指针，所有关键字都在子结点中出现，非子结点作为子结点的索引；B+树总是到子结点才命中；

B*树：（寻道）在B+树基础上，为非子结点也增加链表指针，将结点的最低利用率从1/2提高到2/3；

LSM树：（传输） 在 B+树 基础上， 将读写分离、读操作先内存后磁盘、数据写操作（包括插入、修改、删除也是写）都在内存中进行。到达一定阈值的时候才会刷新到磁盘上。（HBase 刷新到 memStore me） 在大规模情况下，寻道明显比传输低效。

(从磁盘使用方面讲，有两种不同的数据库范式：一种是寻道，一种是传输) RDBMS 通常都是寻道型的。主要是用于存储数据的B树 或 B+ 树结构引起的。 在磁盘寻道的速率级别上实现各种操作，通常每个访问需要 log(N)个寻道操作。

God has given me a gift. Only one. I am the most complete fighter in the world. My whole life, I have trained. I must prove I am worthy of someting.                                                             rocky_24

 

 

 

 

 

 

 

 

 

来自为知笔记(Wiz)