POJ3249 Test for Job(拓扑排序+dp)

Test for Job

Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 10137		Accepted: 2348

Description

Mr.Dog was fired by his company. In order to support his family, he must find a new job as soon as possible. Nowadays, It's hard to have a job, since there are swelling numbers of the unemployed. So some companies often use hard tests for their recruitment.

The test is like this: starting from a source-city, you may pass through some directed roads to reach another city. Each time you reach a city, you can earn some profit or pay some fee, Let this process continue until you reach a target-city. The boss will
compute the expense you spent for your trip and the profit you have just obtained. Finally, he will decide whether you can be hired.

In order to get the job, Mr.Dog managed to obtain the knowledge of the net profit V_i of all cities he may reach (a negative V_i indicates that money is spent rather than gained) and the connection between cities. A
city with no roads leading to it is a source-city and a city with no roads leading to other cities is a target-city. The mission of Mr.Dog is to start from a source-city and choose a route leading to a target-city through which he can get the maximum profit.

Input

The input file includes several test cases. 

The first line of each test case contains 2 integers n and m(1 ≤ n ≤ 100000, 0 ≤ m ≤ 1000000) indicating the number of cities and roads. 

The next n lines each contain a single integer. The ith line describes the net profit of the city i, V_i (0 ≤ |V_i| ≤ 20000) 

The next m lines each contain two integers x, y indicating that there is a road leads from city x to city y. It is guaranteed that each road appears exactly once, and there is no way to return to a previous city. 

Output

The output file contains one line for each test cases, in which contains an integer indicating the maximum profit Dog is able to obtain (or the minimum expenditure to spend)

Sample Input

6 5
1
2
2
3
3
4
1 2
1 3
2 4
3 4
5 6

Sample Output

7

Hint

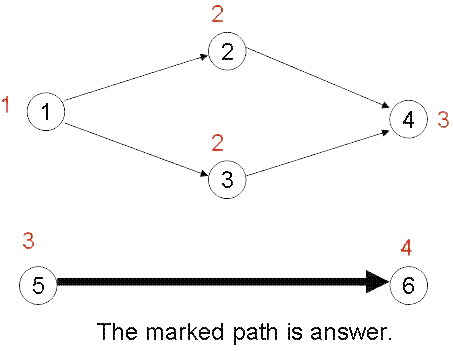
题目链接:点击打开链接

给出n个点的权值和m条路径, 问一条路的最大权值是多少.

起点入度为0, 对全部入度为0的点赋值到dp数组, 进行拓扑排序, 最后遍历出度为0的点, 求得最大值.

AC代码:

#include "iostream"
#include "cstdio"
#include "cstring"
#include "algorithm"
#include "queue"
#include "stack"
#include "cmath"
#include "utility"
#include "map"
#include "set"
#include "vector"
#include "list"
#include "string"
using namespace std;
typedef long long ll;
const int MOD = 1e9 + 7;
const int INF = 0x3f3f3f3f;
const int MAXN = 1e5 + 5;
int n, m, num;
int cost[MAXN], in[MAXN], out[MAXN], head[MAXN], dp[MAXN];
bool vis[MAXN];
struct node
{
	/* data */
	int fr, to, nxt;
}e[MAXN * 10];
void add(int x, int y)
{
	e[num].fr = x;
	e[num].to = y;
	e[num].nxt = head[x];
	head[x] = num++;
}
void toposort()
{
	int cnt = 1;
	while(cnt < n) {
		for(int i = 1; i <= n; ++i)
			if(in[i] == 0 && !vis[i]) {
				vis[i] = true;
				cnt++;
				for(int j = head[i]; j != -1; j = e[j].nxt) {
					int x = e[j].to;
					in[x]--;
					if(dp[i] + cost[x] > dp[x]) dp[x] = dp[i] + cost[x];
				}
			}
	}
}
int main(int argc, char const *argv[])
{
	while(scanf("%d%d", &n, &m) != EOF) {
		memset(in, 0, sizeof(in));
		memset(out, 0, sizeof(out));
		memset(head, -1, sizeof(head));
		memset(vis, false, sizeof(vis));
		num = 1;
		for(int i = 1; i <= n; ++i)
			scanf("%d", &cost[i]);
		for(int i = 1; i <= m; ++i) {
			int x, y;
			scanf("%d%d", &x, &y);
			add(x, y);
			in[y]++;
			out[x]++;
		}
		for(int i = 1; i <= n; ++i)
			if(in[i] == 0) dp[i] = cost[i];
			else dp[i] = -INF;
		toposort();
		int ans = -INF;
		for(int i = 1; i <= n; ++i)
			if(out[i] == 0 && dp[i] > ans) ans = dp[i];
		printf("%d\n", ans);
	}
	return 0;
}