[JZOJ 5894] [NOIP2018模拟10.5] 同余方程 解题报告（容斥）

题目链接：

http://172.16.0.132/senior/#contest/show/2523/0

题目：

题解：（部分内容来自https://blog.csdn.net/gmh77/article/details/82947340）

首先我们容斥一下，设calc(l,r)为i∈[1,l],j∈[q,r]的方程的解的个数，显然答案等于calc(r2,r1)-calc(l1-1,r2)-calc(r1,l2-1)+calc(l1-1,l2-1)

考虑如何计算calc(l,r)

对于l和r，从低位向高位枚举每一个二进制位1，强制把这个1改成0，这样可以保证得到的数小于原来的数并且没有算重。假设l改变第i位，r改变第j位

（假设l不同的位比r后）

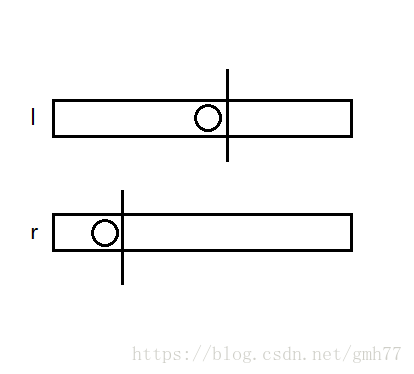
那么用红框表示已知部分，蓝框表示未知部分

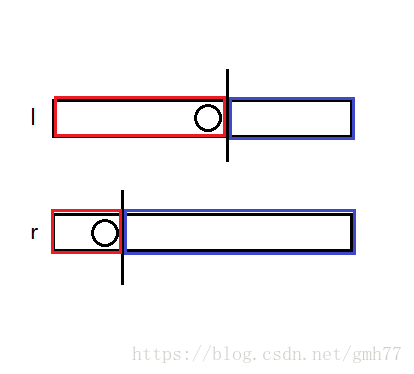
所以异或之后就会变成这样

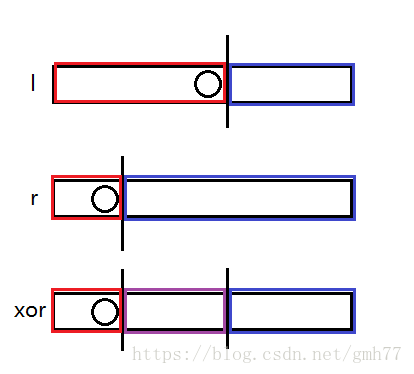
中间的紫色部分表示一半已知，一半未知，后面的蓝色部分表示完全未知

---

显然未知部分可以取到任何可能

考虑中间的紫色部分，由于$a$紫色部分确定，$b$紫色部分不确定，那么对于每一个$b$的紫色部分都对应一个$c$的紫色部分

也就是说，每一个$b$确定$2^{蓝色部分长度}$个$c$，且我们一共有$2^{max(i,j)}-1$个$b$。由于未知部分可以取到任何可能，所以我们一共有$2^{max(i,j)}-1$个$c$

考虑到每个c肯定是平等的，那么每个c就被计算了$\frac{2^{蓝色部分长度} \times (2^{max(i,j)}-1)}{2^{max(i,j)}-1}=2^{蓝色部分长度}$次

$mx=max(i,j)$,发现c的取值就是[((S/p[mx])*mx)^p[mx],((S/p[mx])*mx)^p[mx]+p[mx]-1],p[mx]=1<<mx

注意到第mx位是需要和原来相反的，所以要^p[mx]

---

还有三种情况

1.i==j

这个其实差不多，只是第mx位不需要取反，也就是不需要^p[mx]

2.a或b不改任何一位

这个也是一样的，注意一下变的那一个枚举的任何一位都需要取反

3.a和b都不变

这个直接异或一下直接判断就是了

#include<cstring>
#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;

const int N=;
const int mod=;
ll m;
ll bin[N],p[N];
int a[N],b[N];
ll get(ll l,ll r)
{
    if (l>r) return ;
    if (l) return (r/m-(l-)/m)%mod;
    else return (r/m+)%mod;//要考虑0
}
ll calc(ll l,ll r)
{
    int A=-,B=-;
    ll res=,S=l^r;
    while (l)
    {
        a[++A]=l&;
        l>>=;
    }
    while (r)
    {
        b[++B]=r&;
        r>>=;
    }
    for (int i=;i<=A;i++)
    if (a[i]) res=(res+get(((S/p[i])*p[i])^p[i],((S/p[i])*p[i])^p[i]+p[i]-))%mod;//b不变
    for (int i=;i<=B;i++)
    if (b[i]) res=(res+get(((S/p[i])*p[i])^p[i],((S/p[i])*p[i])^p[i]+p[i]-))%mod;//a不变
    for (int i=;i<=A;i++)
        if (a[i])
            for (int j=;j<=B;j++)
                if (b[j])
                {
                    int mx=max(i,j);//特判i==j
                    if (i!=j) res=(res+get(((S/p[mx])*p[mx])^p[mx],((S/p[mx])*p[mx])^p[mx]+p[mx]-)*bin[min(i,j)])%mod;
                    else res=(res+get(((S/p[mx])*p[mx]),((S/p[mx])*p[mx])+p[mx]-)*bin[min(i,j)])%mod;
                }
    return res+((S%m)==);//i==l&&j==r
}
int main()
{
    freopen("mod.in","r",stdin);
    freopen("mod.out","w",stdout);
    p[]=;bin[]=;
    for (int i=;i<N;i++)
    {
        p[i]=p[i-]<<;
        bin[i]=p[i]%mod;
    }
    ll l1,r1,l2,r2;
    scanf("%lld%lld%lld%lld%lld",&l1,&r1,&l2,&r2,&m);
    printf("%lld\n",((calc(r1,r2)-calc(l1-,r2)-calc(r1,l2-)+calc(l1-,l2-))%mod+mod)%mod);
    return ;
}