[luogu1772 ZJOI2006] 物流运输 (最短路线性dp)

题目描述

物流公司要把一批货物从码头A运到码头B。由于货物量比较大，需要n天才能运完。货物运输过程中一般要转停好几个码头。物流公司通常会设计一条固定的运输路线，以便对整个运输过程实施严格的管理和跟踪。由于各种因素的存在，有的时候某个码头会无法装卸货物。这时候就必须修改运输路线，让货物能够按时到达目的地。但是修改路线是—件十分麻烦的事情，会带来额外的成本。因此物流公司希望能够订一个n天的运输计划，使得总成本尽可能地小。

输入输出格式

输入格式：

第一行是四个整数n(l≤n≤100)、m(l≤m≤20)、K和e。n表示货物运输所需天数，m表示码头总数，K表示每次修改运输路线所需成本，e表示航线条数。接下来e行每行是一条航线描述，包括了三个整数，依次表示航线连接的两个码头编号以及航线长度(>0)。其中码头A编号为1，码头B编号为m。单位长度的运输费用为1。航线是双向的。再接下来一行是一个整数d，后面的d行每行是三个整数P(1<P<m)，a，b(1≤a≤b≤n)。表示编号为P的码头从第a天到第b天无法装卸货物（含头尾）。同一个码头有可能在多个时间段内不可用。但任何时间都存在至少一条从码头A到码头B的运输路线。

输出格式：

包括了一个整数表示最小的总成本。总成本=n天运输路线长度之和+K*改变运输路线的次数。

输入输出样例

输入样例#1：

5 5 10 8

1 2 1

1 3 3

1 4 2

2 3 2

2 4 4

3 4 1

3 5 2

4 5 2

4

2 2 3

3 1 1

3 3 3

4 4 5

输出样例#1：

32

说明

【样例输入说明】

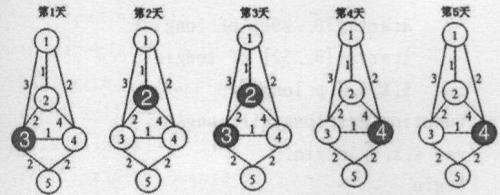
上图依次表示第1至第5天的情况，阴影表示不可用的码头。

【样例输出说明】

前三天走1-4-5，后两天走1-3-5，这样总成本为(2+2)3+(3+2)2+10=32。

_NOI导刊2010提高（01）

最短路的应用好题。。

先把每段时间的最短路求出来然后一个简单dp就好了

code:

//By Menteur_Hxy
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <map>
#include <vector>
#include <queue>
#include <set>
#include <ctime>
#define M(a,b) memset(a,(b),sizeof(a))
#define F(i,a,b) for(register int i=(a);i<=(b);i++)
#define LL long long
using namespace std;
inline LL rd() {
	LL x=0,fla=1; char c=' ';
	while(c>'9'|| c<'0') {if(c=='-') fla=-fla; c=getchar();}
	while(c<='9' && c>='0') x=x*10+c-'0',c=getchar();
	return x*fla;
}
inline void out(LL x){
    int a[25],wei=0;
    if(x<0) putchar('-'),x=-x;
    for(;x;x/=10) a[++wei]=x%10;
    if(wei==0){ puts("0"); return;}
    for(int j=wei;j>=1;--j) putchar('0'+a[j]);
    putchar('\n');
}
const int N=110;
const int INF=0x3f3f3f3f;
int n,m,k,e,d,cnt;
int v[N][N],dis[N],ex[N],head[N],f[N][N],vis[N],exi[N];
LL dp[N];
struct edges{
	int next,to,w;
}edg[N*N*2];
void add(int a,int b,int c) {
	edg[++cnt].next=head[a];
	edg[cnt].to=b;
	edg[cnt].w=c;
	head[a]=cnt;
}
queue <int> q;
int spfa(int a,int b) {
	M(vis,0);
	M(dis,0x3f);
	F(i,1,m) exi[i]=1;
	F(i,1,m) F(j,a,b) if(v[i][j]) exi[i]=0;
	q.push(1);vis[1]=1;dis[1]=0;
	while(!q.empty()) {
		int u=q.front(); q.pop(); vis[u]=0;
		for(int i=head[u];i;i=edg[i].next) {
			int t=edg[i].to;
			if(!exi[t]) continue;
			if(dis[u]+edg[i].w<dis[t]) {
				dis[t]=dis[u]+edg[i].w;
				if(!vis[t]) q.push(t),vis[t]=1;
			}
		}
	}
	return dis[m];
}
int main() {
	n=rd(),m=rd(),k=rd(),e=rd();
	F(i,1,e) {
		int a=rd(),b=rd(),c=rd();
		add(a,b,c);
		add(b,a,c);
	}
	d=rd();
	F(i,1,d) {
		int p=rd(),x=rd(),y=rd();
		for(x;x<=y;x++) v[p][x]=1;
	}
	F(i,1,n) F(j,1,n) f[i][j]=spfa(i,j);
	F(i,1,n) {
		dp[i]=(LL)f[1][i]*i;
		F(j,1,i-1)
			dp[i]=min(dp[i],dp[j]+k+(LL)f[j+1][i]*(i-j));
	}
	out(dp[n]);
	return 0;
}