平衡二叉树AVL删除

平衡二叉树的插入过程:http://www.cnblogs.com/hujunzheng/p/4665451.html

对于二叉平衡树的删除采用的是二叉排序树删除的思路:

　　假设被删结点是*p，其双亲是*f，不失一般性，设*p是*f的左孩子，下面分三种情况讨论：
　　⑴ 若结点*p是叶子结点，则只需修改其双亲结点*f的指针即可。
　　⑵ 若结点*p只有左子树PL或者只有右子树PR，则只要使PL或PR 成为其双亲结点的左子树即可。
　　⑶ 若结点*p的左、右子树均非空，先找到*p的中序前趋结点*s（注意*s是*p的左子树中的最右下的结点，它的右链域为空），然后有两种做法：
　　　　① 令*p的左子树直接链到*p的双亲结点*f的左链上,而*p的右子树链到*p的中序前趋结点*s的右链上。
　　　　② 以*p的中序前趋结点*s代替*p（即把*s的数据复制到*p中），将*s的左子树链到*s的双亲结点*q的左（或右）链上。

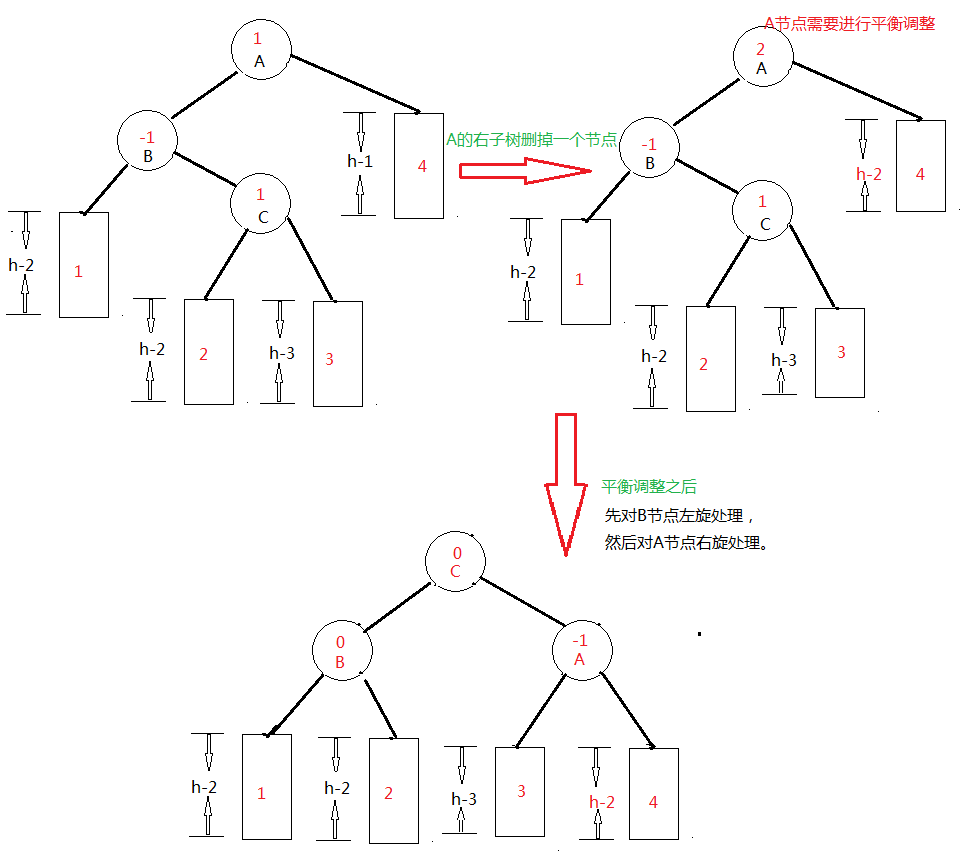
注：leftBalance_del 和 rightBalance_del方法是在删除节点时对左子树和右子树的平衡调整，leftBalance 和 rightBalance方法是在插入节点是对左右子树的平衡调整。 在具体调整的时候，和插入式调整时运用同样的分类方法，这里介绍一种情况，如下图所示（代码部分见代码中的提示）

#include<iostream>
#include<cstring>
#include<string>
#include<queue>
#include<map>
#include<cstdio>
#define LH 1 //左高
#define EH 0 //等高
#define RH -1 //右高
using namespace std;

template <typename ElemType>
class BSTNode{
    public:
        ElemType data;//节点的数据
        int bf;//节点的平衡因子
        BSTNode *child[];
        BSTNode(){
            child[] = NULL;
            child[] = NULL;
        }
};

typedef BSTNode<string> BSTnode, *BSTree;

template <typename ElemType>
class AVL{
    public:
        BSTNode<ElemType> *T;
        void buildT();
        void outT(BSTNode<ElemType> *T);
        void deleteAVL(BSTNode<ElemType>* &T, ElemType key, bool &shorter);
        bool insertAVL(BSTNode<ElemType>* &T, ElemType key, bool &taller);
    private:
        void deleteNode(BSTNode<ElemType>* T, BSTNode<ElemType>* &s, BSTNode<ElemType>* p, bool flag, bool &shorter);
        void rotateT(BSTNode<ElemType>* &o, int x);//子树的左旋或者右旋
        void leftBalance(BSTNode<ElemType>* &o);
        void rightBalance(BSTNode<ElemType>* &o);

        void leftBalance_del(BSTNode<ElemType>* &o);
        void rightBalance_del(BSTNode<ElemType>* &o);
};

template <typename ElemType>
void AVL<ElemType>::rotateT(BSTNode<ElemType>* &o, int x){
    BSTNode<ElemType>* k = o->child[x^];
    o->child[x^] = k->child[x];
    k->child[x] = o;
    o = k;
}

template <typename ElemType>
void AVL<ElemType>::outT(BSTNode<ElemType> *T){
    if(!T) return;
    cout<<T->data<<" ";
    outT(T->child[]);
    outT(T->child[]);
}

template <typename ElemType>
void AVL<ElemType>::buildT(){
   T = NULL;
   ElemType key;
   while(cin>>key){
           if(key==) break;
           bool taller = false;
           insertAVL(T, key, taller);
   }
}

template <typename ElemType>
void AVL<ElemType>::deleteNode(BSTNode<ElemType>* T, BSTNode<ElemType>* &s, BSTNode<ElemType>* p, bool flag, bool &shorter){
    if(flag){
        flag = false;
        deleteNode(T, s->child[], s, flag, shorter);
        if(shorter){
            switch(s->bf){
                case LH:
                    s->bf = EH;
                    shorter = false;
                    break;
                case EH:
                    s->bf = RH;
                    shorter = true;
                    break;
                case RH:
                    rightBalance_del(s);
                    shorter = false;
                    break;
            }
        }
    } else {
        if(s->child[]==NULL){
            T->data = s->data;
            BSTNode<ElemType>* ss = s;
            if(p != T){
                p->child[] = s->child[];
            } else {
                p->child[] = s->child[];
            }
            delete ss;//s是引用类型，不能delete s
            shorter = true;
            return ;
        }
        deleteNode(T, s->child[], s, flag, shorter);
        if(shorter){
            switch(s->bf){
                case LH://这是上面配图的情况
                    leftBalance_del(s);
                    shorter = false;
                    break;
                case EH:
                    s->bf = LH;
                    shorter = true;
                    break;
                case RH:
                    s->bf = EH;
                    shorter = false;
                    break;
            }
        }
    }
} 

template <typename ElemType>
bool AVL<ElemType>::insertAVL(BSTNode<ElemType>* &T, ElemType key, bool &taller){
    if(!T){//插入新的节点，taller=true 那么树的高度增加
        T = new BSTNode<ElemType>();
        T->data = key;
        T->bf = EH;
        taller = true;
    } else {
        if(T->data == key){
            taller = false;
            return false;
        }
        if(T->data > key){//向T的左子树进行搜索并插入
            if(!insertAVL(T->child[], key, taller)) return false;
            if(taller){//
                switch(T->bf){
                    case LH://此时左子树的高度高，左子树上又插入了一个节点，失衡，需要进行调整
                        leftBalance(T);
                        taller = false;//调整之后高度平衡
                        break;
                    case EH:
                        T->bf = LH;
                        taller = true;
                        break;
                    case RH:
                        T->bf = EH;
                        taller = false;
                        break;
                }
            }
        }
        if(T->data < key) {//向T的右子树进行搜索并插入
            if(!insertAVL(T->child[], key, taller)) return false;
            switch(T->bf){
                case LH:
                    T->bf = EH;
                    taller = false;
                    break;
                case EH:
                    T->bf = RH;
                    taller = true;
                    break;
                case RH:
                    rightBalance(T);
                    taller = false;
                    break;
            }
        }
    }
    return true;
}

template <typename ElemType>
void AVL<ElemType>::deleteAVL(BSTNode<ElemType>* &T, ElemType key, bool &shorter){
    if(T->data == key){
        BSTNode<ElemType>*q, s;
        if(!T->child[]){//右子树为空，然后重接其左子树
            q = T;
            T = T->child[];
            shorter = true;//树变矮了
            delete q;
        } else if(!T->child[]){//左子树为空，重接其右子树
            q = T;
            T = T->child[];
            shorter = true;//树变矮了
            delete q;
        } else {//左右子树都非空 ，也就是第三种情况 
            deleteNode(T, T, NULL, true, shorter);
            shorter = true;
        }
    } else if(T->data > key) {//左子树
        deleteAVL(T->child[], key, shorter);
        if(shorter){
            switch(T->bf){
                case LH:
                    T->bf = EH;
                    shorter = false;
                    break;
                case RH:
                    rightBalance_del(T);
                    shorter = false;
                    break;
                case EH:
                    T->bf = RH;
                    shorter = true;
                    break;
            }
        }
    } else if(T->data < key){//右子树
        deleteAVL(T->child[], key, shorter);
        if(shorter){
            switch(T->bf){
                case LH://这是上面配图的情况
                    leftBalance_del(T);
                    shorter = false;
                    break;
                case RH:
                    T->bf = EH;
                    shorter = false;
                    break;
                case EH:
                    T->bf = LH;
                    shorter = true;
                    break;
            }
        }
    }
}

template <typename ElemType>
void AVL<ElemType>::leftBalance(BSTNode<ElemType>* &T){
    BSTNode<ElemType>* lchild = T->child[];
    switch(lchild->bf){//检查T的左子树的平衡度，并作相应的平衡处理
        case LH://新节点 插入到 T的左孩子的左子树上，需要对T节点做单旋(右旋)处理
            T->bf = lchild->bf = EH;
            rotateT(T, );
            break;
        case RH://新节点 插入到 T的左孩子的右子树上，需要做双旋处理  1.对lchild节点进行左旋，2.对T节点进行右旋
            BSTNode<ElemType>* rdchild = lchild->child[];
            switch(rdchild->bf){//修改 T 及其左孩子的平衡因子
                case LH: T->bf = RH; lchild->bf = EH; break;
                case EH: T->bf = lchild->bf = EH; break;//发生这种情况只能是 rdchild无孩子节点
                case RH: T->bf = EH; lchild->bf = LH; break;
            }
            rdchild->bf = EH;
            rotateT(T->child[], );//不要写成 rotateT(lc, 0);//这样的话T->lchild不会改变
            rotateT(T, );
            break;
    }
}

template <typename ElemType>
void AVL<ElemType>::rightBalance(BSTNode<ElemType>* &T){
    BSTNode<ElemType>* rchild = T->child[];
    switch(rchild->bf){//检查T的左子树的平衡度，并作相应的平衡处理
        case RH://新节点 插入到 T的右孩子的右子树上，需要对T节点做单旋(左旋)处理
            T->bf = rchild->bf = EH;
            rotateT(T, );
            break;
        case LH://新节点 插入到 T的右孩子的左子树上，需要做双旋处理  1.对rchild节点进行右旋，2.对T节点进行左旋
            BSTNode<ElemType>* ldchild = rchild->child[];
            switch(ldchild->bf){//修改 T 及其右孩子的平衡因子
                case LH: T->bf = EH; rchild->bf = RH; break;
                case EH: T->bf = rchild->bf = EH; break;//发生这种情况只能是 ldchild无孩子节点
                case RH: T->bf = LH; rchild->bf = EH; break;
            }
            ldchild->bf = EH;
            rotateT(T->child[], );
            rotateT(T, );
            break;
    }
}

template <typename ElemType>
void AVL<ElemType>::leftBalance_del(BSTNode<ElemType>* &T){
    BSTNode<ElemType>* lchild = T->child[];
    switch(lchild->bf){
        case LH:
            T->bf = EH;
            lchild->bf = EH;
            rotateT(T, );
            break;
        case EH:
            T->bf = LH;
            lchild->bf = EH;
            rotateT(T, );
            break;
        case RH://这是上面配图的情况
            BSTNode<ElemType>* rdchild = lchild->child[];
            switch(rdchild->bf){
                case LH:
                    T->bf = RH;
                    lchild->bf = rdchild->bf = EH;
                    break;
                case EH:
                    rdchild->bf = T->bf = lchild->bf = EH;
                    break;
                case RH:
                    T->bf = rdchild->bf = EH;
                    lchild->bf = LH;
                    break;
            }
            rotateT(T->child[], );
            rotateT(T, );
            break;
    }
}

template <typename ElemType>
void AVL<ElemType>::rightBalance_del(BSTNode<ElemType>* &T){
    BSTNode<ElemType>* rchild = T->child[];
    BSTNode<ElemType>* ldchild = rchild->child[];
    switch(rchild->bf){
        case LH:
            switch(ldchild->bf){
                case LH:
                    ldchild->bf = T->bf = EH;
                    rchild->bf = RH;
                    break;
                case EH:
                    ldchild->bf = T->bf = rchild->bf = EH;
                    break;
                case RH:
                    rchild->bf = T->bf = EH;
                    ldchild->bf = LH;
                    break;
            }
            rotateT(T->child[], );
            rotateT(T, );
            break;
        case EH:
            //outT(this->T);e EH:
            T->bf = RH;
            rchild->bf = EH;
            rotateT(T, );
            break;
        case RH:
            T->bf = EH;
            rchild->bf = EH;
            rotateT(T, );
            break;
    }
}

int main(){
    AVL<int> avl;
    avl.buildT();
    cout<<"平衡二叉树先序遍历如下:"<<endl;
    avl.outT(avl.T);
    cout<<endl;
    bool shorter = false;
    avl.deleteAVL(avl.T, , shorter);
    avl.outT(avl.T);
    return ;
} 

/*
 13 24 37 90 53 0

 13 24 37 90 53 12 26 0
*/