Matlab--从入门到精通（Chapter3 矩阵运算）

      数值计算可以分为两类：矩阵运算和矩阵元素运算

3.1 矩阵函数和特殊矩阵

       矩阵代数的处理数组大部分以一维数组（向量）和二维数组（矩阵）为主。

常见的矩阵处理函数如下：

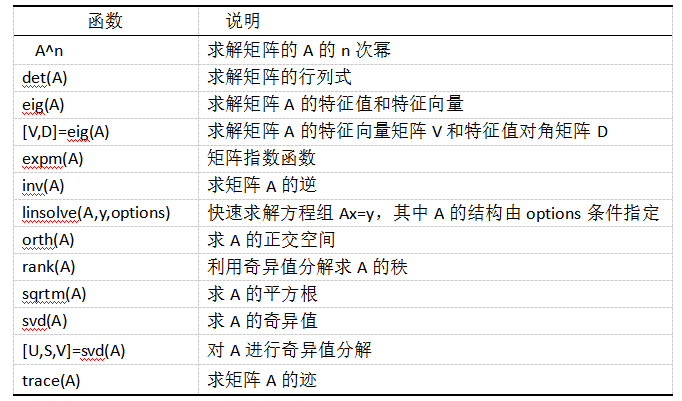
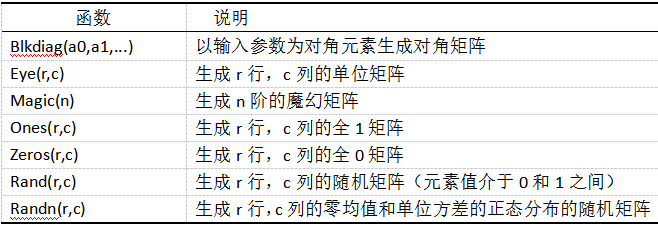
特殊矩阵：

稀疏矩阵：

稀疏矩阵的创建通常可以通过使用sparse和spdiags函数来进行：

• sparse(i,j,s,m,n,nz_max)使用[i,j,s]来创建m*n维稀疏矩阵s，其中s为所有非零元素构成的向量，i，j分别为非零元素的行下标和列下标。
• spdiags（B，d,m,n）可以抽取、创建或替代对角稀疏矩阵，其中m和n分别为矩阵的行和列的维数，d表示长度为p的整数向量，B为满矩阵。
• 稀疏矩阵和满矩阵之间可以通过sparse和full函数进行转换。
• spy(A)画出A矩阵

3-2  矩阵分析

• 范数分析：norm()函数可以用来求解向量和矩阵的范数，

           如 n2=norm(x),ninf=norm(x,inf）,nneg_inf=norm(x,-inf)分别求解二范数，无穷范数和负无穷范数

          求解大型矩阵的范数和稀疏矩阵时，可以考虑采用normest来求解。

• 条件数分析：矩阵的条件数总是大于1，正交矩阵的条件数等于1，奇异矩阵的条件数为无穷大，

         病态矩阵的条件数是比较大的数据。 矩阵的条件数可以通过函数cond()求解。

3.3  线性方程组

下面介绍三种方程组：恰定方程组、超定方程组、欠定方程组。

•  恰定方程组：方程组的个数和未知数的个数相等，分为奇异和非奇异两种。

%求解非奇异恰定方程组的解
>> A=[1 2 3;4 5 6;7 8 0];
>> y=[366;804;351]

%方法一：判断A的条件数、秩以及增广矩阵[A y]的秩
>> rank(A)

>>rank([A y])

>> cond(A)

>> x_1=inv(A)*y

>> %方法2 通过矩阵左除来求解线性方程组的解,LU分解，速度快
>> x_2=A\y

%求解奇异恰定方程组的解

>> A=[1 3 7;-1 4 4;1 10 18];
>> y=[6;4;15];
>> %方法1:通过矩阵左除来求解线性方程组的解
>> x_1=A\y

>> %方法2 判断A的条件数、A的秩以及增广矩阵[A y]的秩
>> det_A=det(A)

>> rank_A=rank(A)

>> rank_Ay=rank([A y])

>> cond_A=cond(A)

>> x_2=pinv(A)*y;
>> disp(x_2)

•  欠定方程组：方程组的个数小于未知数的个数，存在无数个解。最小范数解，略。

方法1：左除法：x_1=A\y

方法2：伪逆矩阵法（范数最小）

x_2=pinv(A)*y

•  超定方程组：方程组的个数大于未知数的个数，存在无数个解。最小二乘解，略。

3.4  矩阵分解

   主要包括Cholesky 分解、LU分解和QR分解

3.5 特征值分析(略)