理论知识：

第四范式自主研发算法GBDT(Gradient Boosting Decision Tree)

GBDT是一种基分类器为决策树的集成学习方法。决策树是一种常见的机器学习算法，GBDT中使用到的是回归树，如下图所示，回归树包含一个根结点、若干个内部结点和若干个叶子结点，每个叶子结点对应于一个实数值的预测结果，其他每个结点对应于一个特征判断，根结点包含所有样本，每个结点包含的样本集合根据特征判断的结果被分到子结点中。

GBDT模型是一个由很多棵树组成的决策森林，预测结果是所有决策树的预测结果加权之和。

目标函数
形式上，GBDT可以表示为

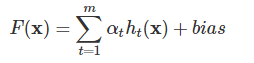
其中ht(x)ht(x)是第t个回归树αt，是第t个回归树的权重bias，bias是偏差项。GBDT的学习过程可以看作迭代式函数梯度下降过程，每次迭代学习一个拟合负梯度方向的基分类器

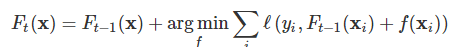
对其中的优化问题做一步梯度下降迭代

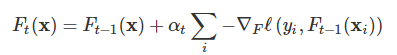
其中

其中Ft(x)是第t轮的模型，是损失函数，先知系统里面使用的是常见的对数几率损失函数

其中y是样本真实标记，是预测标记。

优化算法

GBDT使用的基分类器是回归树，每颗回归树用于拟合梯度下降中的梯度值。先知中回归树的学习目标是均方误差

其中为第t轮第i个样本的梯度值。回归树学习完之后，根据树的结果，解一个简单的优化问题，更新。

实现连接

GDBT的更多相关文章

  1. gdbt与adboost(或者说boosting)区别

    boosting 是一种将弱分类器转化为强分类器的方法统称,而adaboost是其中的一种,或者说AdaBoost是Boosting算法框架中的一种实现 https://www.zhihu.com/q ...

  2. 机器学习-树模型理论（GDBT，xgboost，lightBoost，随机森林）

    tree based ensemble algorithms 主要介绍以下几种ensemble的分类器(tree based algorithms) xgboost lightGBM: 基于决策树算法 ...

  3. gdbt原理解析

    链接: http://note.youdao.com/noteshare?id=aeb1c7a30c5f4b70e3fff51f28ee5c47 懒得复制到这里了,一开始是在有道云笔记上写的,这里的公 ...

  4. xgboost与gdbt的不同和优化

    XGBoost是GBDT算法的一种变种,是一种常用的有监督集成学习算法:是一种 伸缩性强.便捷的可并行构建模型的Gradient Boosting算法 Xgboost和GBDT不同之处 xgboost ...

  5. 机器学习回顾篇（15）：集成学习之GDBT

    .caret, .dropup > .btn > .caret { border-top-color: #000 !important; } .label { border: 1px so ...

  6. GDBT和XGBoost

    https://www.cnblogs.com/pinard/p/6140514.html https://www.cnblogs.com/liuwu265/p/4690486.html https: ...

  7. 梯度提升树(GBDT)原理小结

    在集成学习之Adaboost算法原理小结中,我们对Boosting家族的Adaboost算法做了总结,本文就对Boosting家族中另一个重要的算法梯度提升树(Gradient Boosting De ...

  8. Adaboost\GBDT\GBRT\组合算法

    Adaboost\GBDT\GBRT\组合算法(龙心尘老师上课笔记) 一.Bagging (并行bootstrap)& Boosting(串行) 随机森林实际上是bagging的思路,而GBD ...

  9. 机器学习&数据挖掘笔记_16（常见面试之机器学习算法思想简单梳理）

    前言: 找工作时(IT行业),除了常见的软件开发以外,机器学习岗位也可以当作是一个选择,不少计算机方向的研究生都会接触这个,如果你的研究方向是机器学习/数据挖掘之类,且又对其非常感兴趣的话,可以考虑考 ...

随机推荐

  1. NumPy IO

    NumPy IO Numpy 可以读写磁盘上的文本数据或二进制数据. NumPy 为 ndarray 对象引入了一个简单的文件格式:npy. npy 文件用于存储重建 ndarray 所需的数据.图形 ...

  2. NumPy 字符串函数

    NumPy 字符串函数 以下函数用于对 dtype 为 numpy.string_ 或 numpy.unicode_ 的数组执行向量化字符串操作. 它们基于 Python 内置库中的标准字符串函数. ...

  3. 去7JAVA

    public static void main(String args){ for(int i=1;i<100;i++){ if(i%7!=0 && i %10!=7 & ...

  4. oracle中的to_number在mysql中的转换

    select cast(11 as unsigned int) /*整型*/ select cast(11 as decimal(10,2)) /*浮点型*/ 注:(10,2)代表数字共十位,小数点后 ...

  5. white-space和word-wrap和word-break所表示的换行和不换行的区别

    一.前言 使得文本换行有很多方式, <br/>标签元素,能够强制使得所在位置文本换行 <p>元素,<div>设定宽度,都可以对文本内容实现自适应换行 对于长单词或者 ...

  6. 不包含数据和字母的Webshell

        在做php20中的challenge5时学习到了php中可代替数字和字母的符号,悲剧的是这道题没做出来,目前先整理知识点吧555555555555     情况是:很多时候在敏感地方WAF会阻 ...

  7. win10装回win7。PE下把原来的系统盘格掉，再安装hdd，重启就好了

    win10装回win7.安装文件解压到某盘根目录,然后 PE下把原来的系统盘格掉,再安装hdd,重启就好了

  8. for all entries

    1.必须要判断for all entries in后面的内表是否为空,如果为空,where条件中与内表中字段进行比较的结果全部为真,会导致取出非常多的数据,影响系统性能.2.使用for all ent ...

  9. Bootstrap(10) 进度条媒体对象和 Well 组件

    一．Well 组件这个组件可以实现简单的嵌入效果. <!-- //嵌入效果 --> <div class="well">Bootstrap</div& ...

  10. kalman滤波（一）---对各参数的理解

    一.引言 1.卡尔曼滤波中的真实值,测量值,预测值,估计值怎么区分?他的5条公式是其核心内容,结合现代的计算机,其实卡尔曼的程序相当的简单,只要你理解了他的那5条公式. 用一个简单的小例子:假设我们要 ...